Single-cell RNA-sequencing: variance stabilizing transformations

1 Approximating the variance stabilizing transformation of a Poisson random variable

• A random variable \(Y \sim Poi(\mu)\) has \(Var(Y) = E(Y) = \mu\).
• We are looking for a variance stabilizing transformation (VST) \(f(Y)\) such that \(Var(f(Y)) = c\), with \(c\) any constant. In particular, we need \(Var(f(Y))\) to be independent of \(\mu\).
• A first-order Taylor series gives us \(f(Y) \approx f(\mu) + (Y - \mu) f'(\mu)\).
• Rearranging gives us \(\left\{ f(Y) - f(\mu) \right\}^2 = (Y-\mu)^2 f'(\mu)^2\).
• Which may be written as \(Var(f(Y)) = Var(Y)f'(\mu)^2\).
• This shows us that we want a transformation such that \(f'(\mu)^2 = 1/\mu\) because then \(\forall \mu: Var(f(Y)) = 1\)! Let’s find out.
• The last bullet point can be written as \(f'(\mu) = \frac{1}{\sqrt{\mu}}\) and therefore \(f(\mu) = \int \frac{1}{\sqrt{\mu}} d\mu = 2 \mu^{1/2}\).
• Finally, this shows us that the transformation \(f(Y) = 2 Y^{1/2}\) ensures \(Var(f(Y)) = 1\). Similar, as is often written in the scientific literature, the transformation \(f(Y) = Y^{1/2}\) ensures \(Var(f(Y)) = 1/4\).
• Note that these derivations all rely on the first-order Taylor expansion to be a good approximation. The VST will therefore work better for random variables with a high mean \(\mu\) as the distribution will be more discrete for random variables with a low mean. We show this using simulation below.

set.seed(871)
N <- 1e3
df <- data.frame(mean=rep(NA, N),
                 var=rep(NA, N),
                 transVar=rep(NA, N))
for(kk in 1:N){
  sampledMu <- runif(n=1, min=1, max=500)
  y <- rpois(n=500, lambda=sampledMu)
  df[kk,] <- c(mean(y), var(y), var(sqrt(y)))
}

plot(x=df$mean, y=df$var,
     xlab = "Mean of RV", ylab="Variance of RV")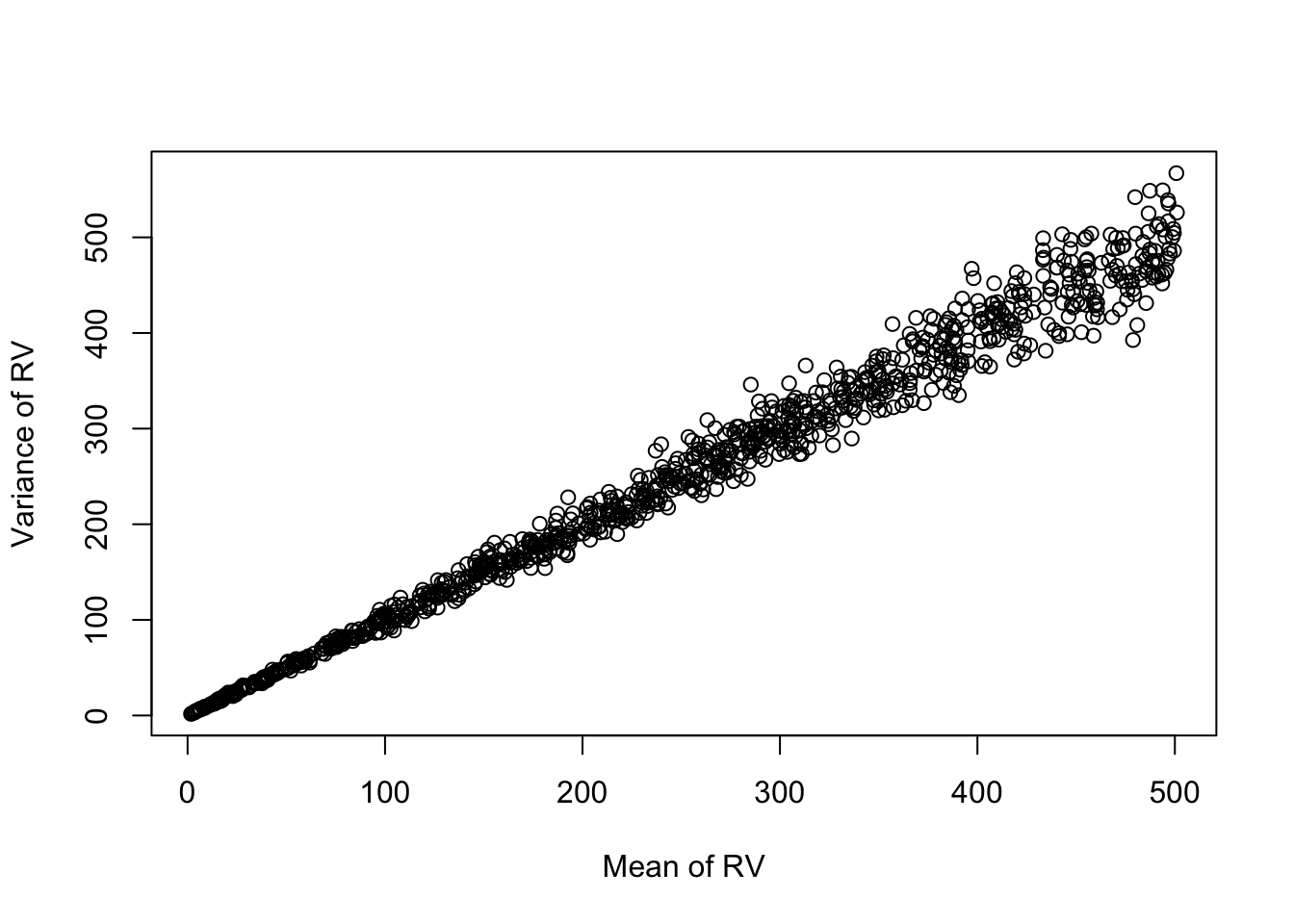

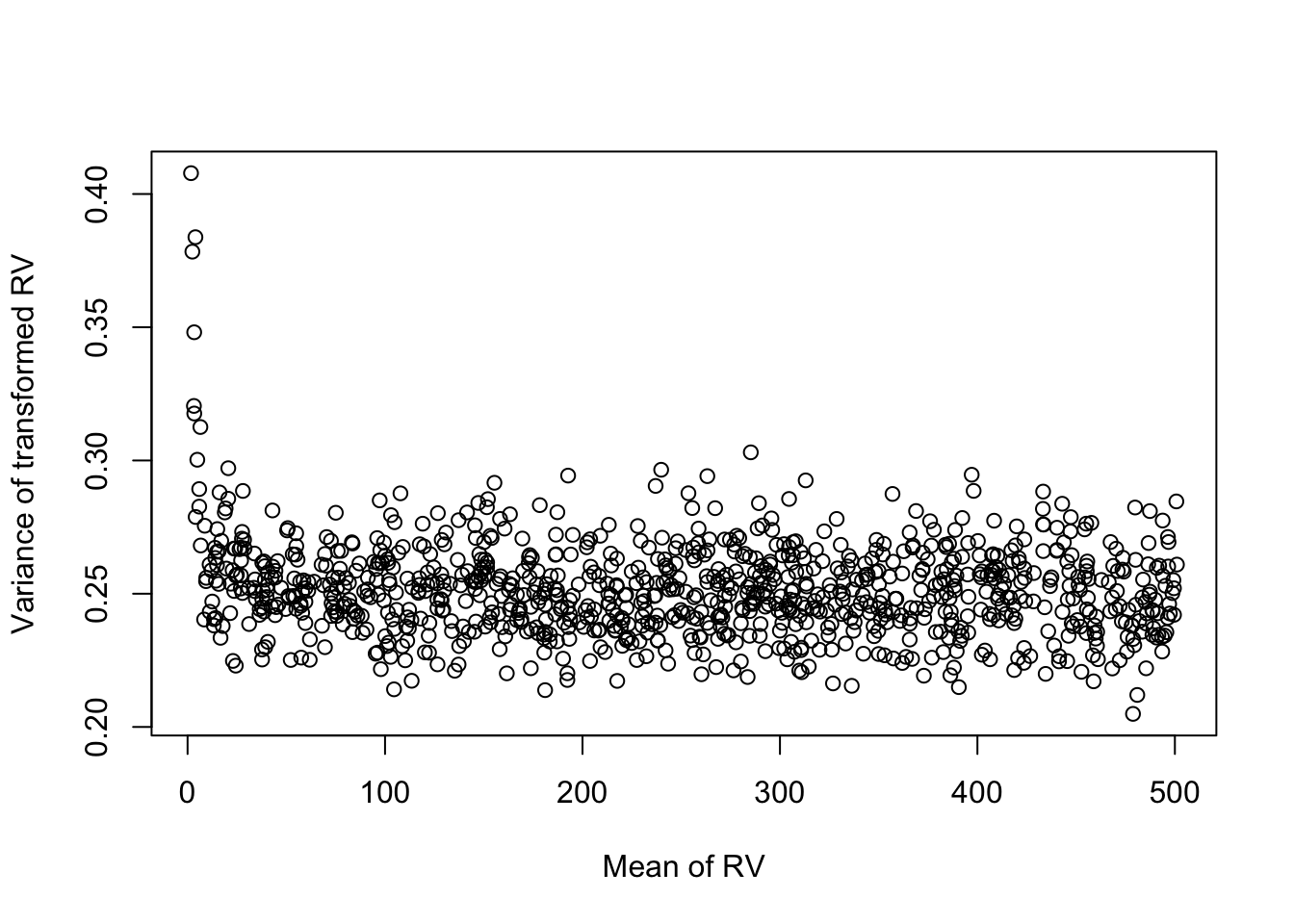
plot(x=df$mean, y=df$transVar,
     xlab = "Mean of RV", ylab="Variance of transformed RV")

Question. Why is the first plot heteroscedastic?

Answer.

Remember that \(Var(\hat{\mu}) = \frac{\hat{\mu}}{n}\). Since for all random variables in our simulation \(n\) is equal, in our case we have that \(Var(\hat{\mu}) = c\hat{\mu}\). The variance on estimating the mean thus increases with the mean.