Sequencing: GLM for gene expression

suppressPackageStartupMessages(library(SummarizedExperiment))
se <- readRDS("data/seParathyroid.rds")

## extract data from one gene
y <- assays(se)$counts[5,]

## extract covariates for each sample
treatment <- colData(se)$treatment
table(treatment)

## treatment
## Control     DPN     OHT 
##       7       8       8

time <- colData(se)$time
table(time)

## time
## 24h 48h 
##  11  12

patient <- colData(se)$patient
table(patient)

## patient
## 1 2 3 4 
## 6 6 6 5

table(patient, treatment, time)

## , , time = 24h
## 
##        treatment
## patient Control DPN OHT
##       1       1   1   1
##       2       1   1   1
##       3       1   1   1
##       4       0   1   1
## 
## , , time = 48h
## 
##        treatment
## patient Control DPN OHT
##       1       1   1   1
##       2       1   1   1
##       3       1   1   1
##       4       1   1   1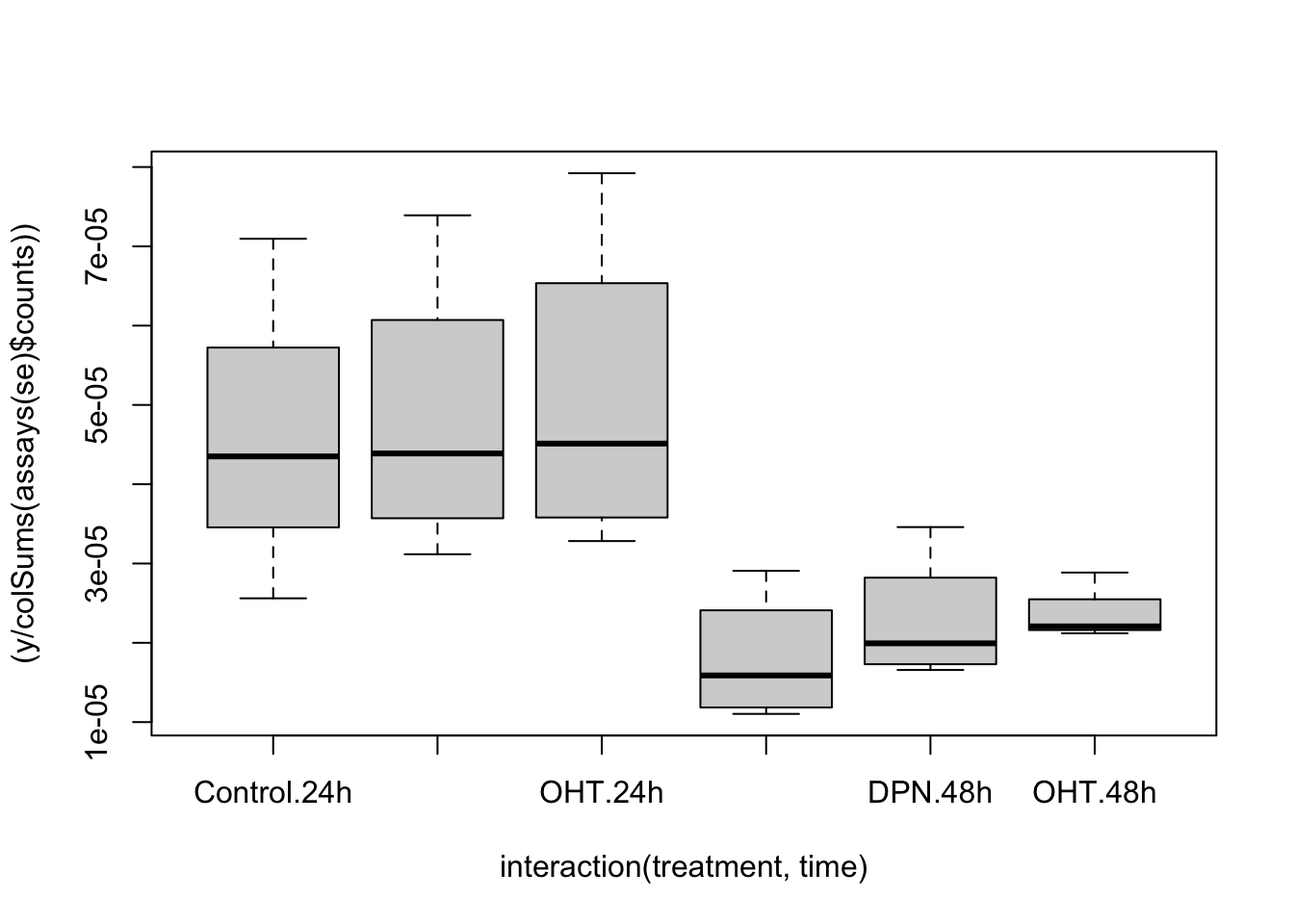

boxplot((y/colSums(assays(se)$counts)) ~ interaction(treatment, time))

## dotplot for each treatment, matching patient samples
df <- data.frame(y=y,
                 treatment=treatment,
                 time=time,
                 patient=patient)
ggplot(df, aes(x=time, y=y)) +
  geom_point() +
  geom_line(aes(group = patient)) + 
  facet_grid(.~treatment) +
  theme_classic()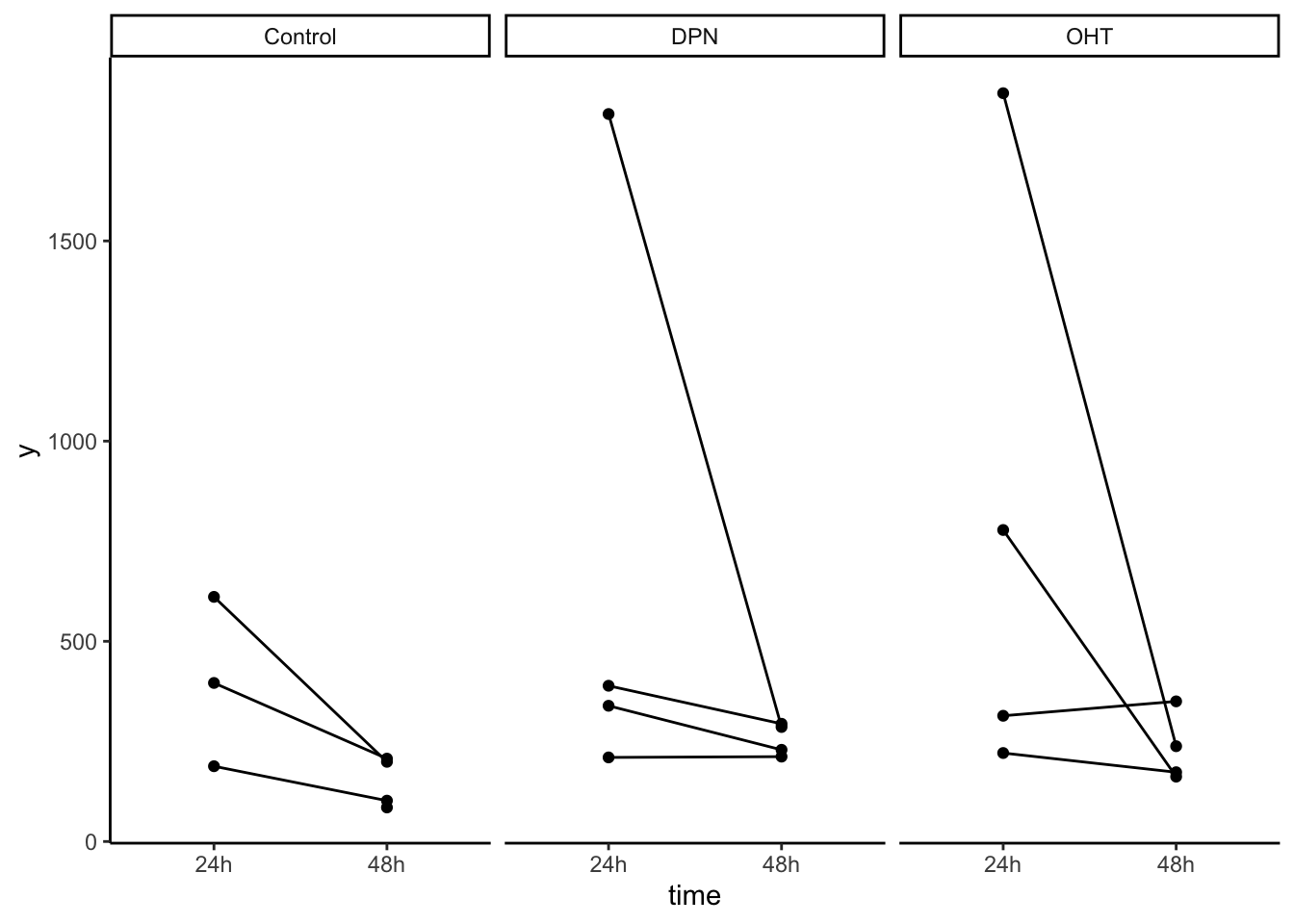

1 Poisson GLM

m <- glm(y ~ treatment*time + patient,
         family = "poisson")
plot(m) # Extra-Poisson variation?

1.1 Check overdispersion

ePearson <- resid(m, type="pearson")
n <- length(y)
p <- length(coef(m))
sum(ePearson^2) / (n-p) # huge overdispersion.

## [1] 115.2631

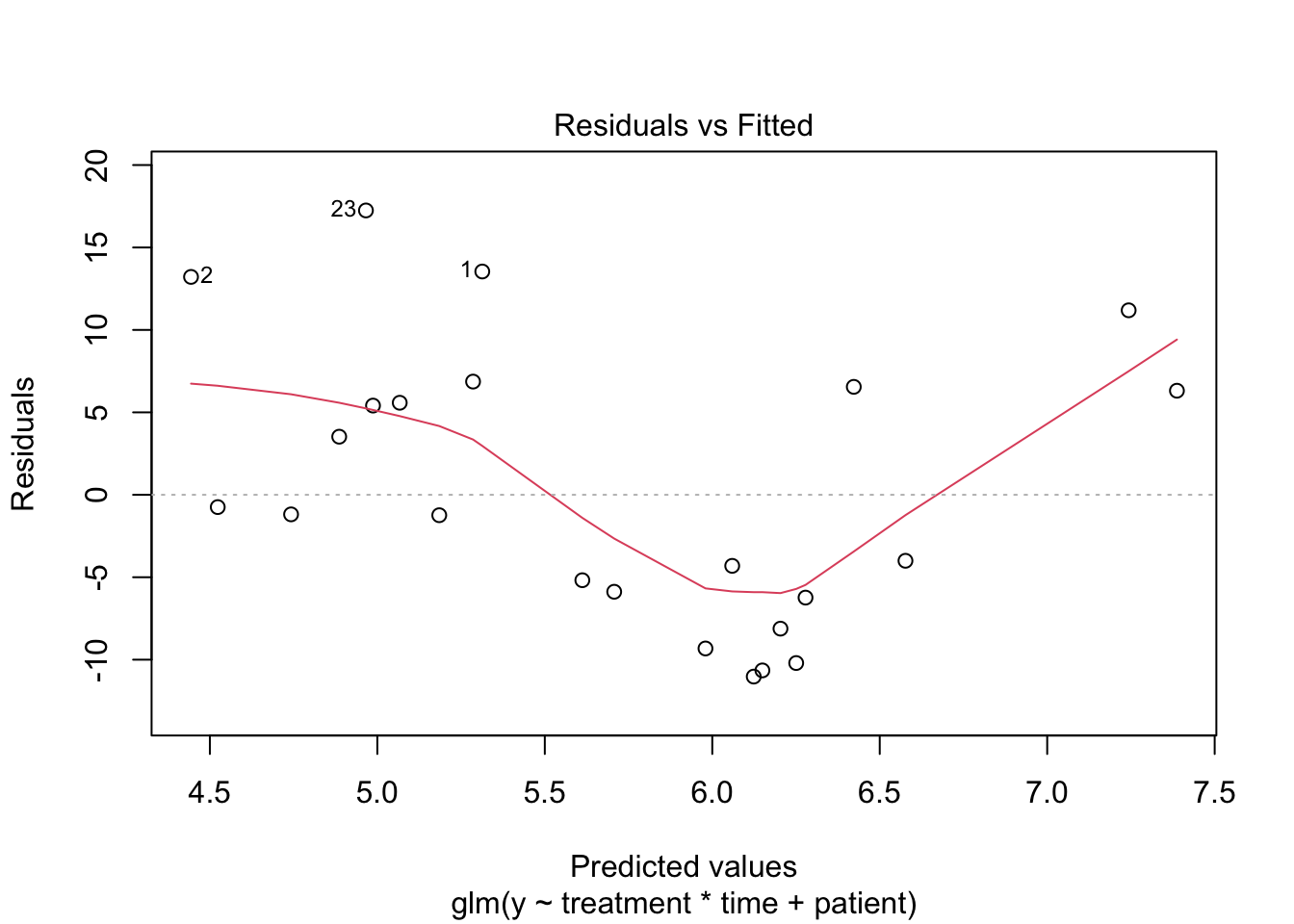
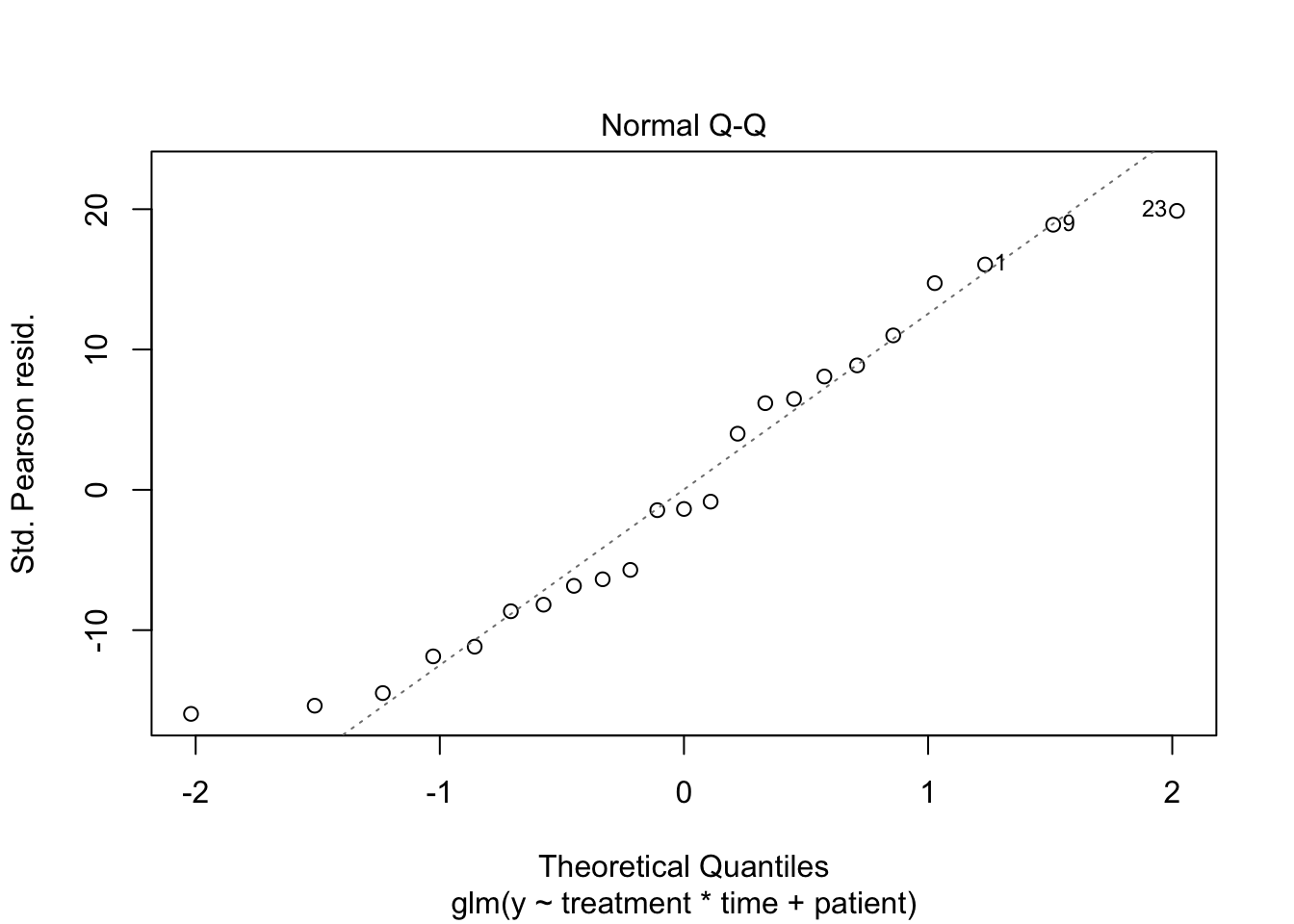
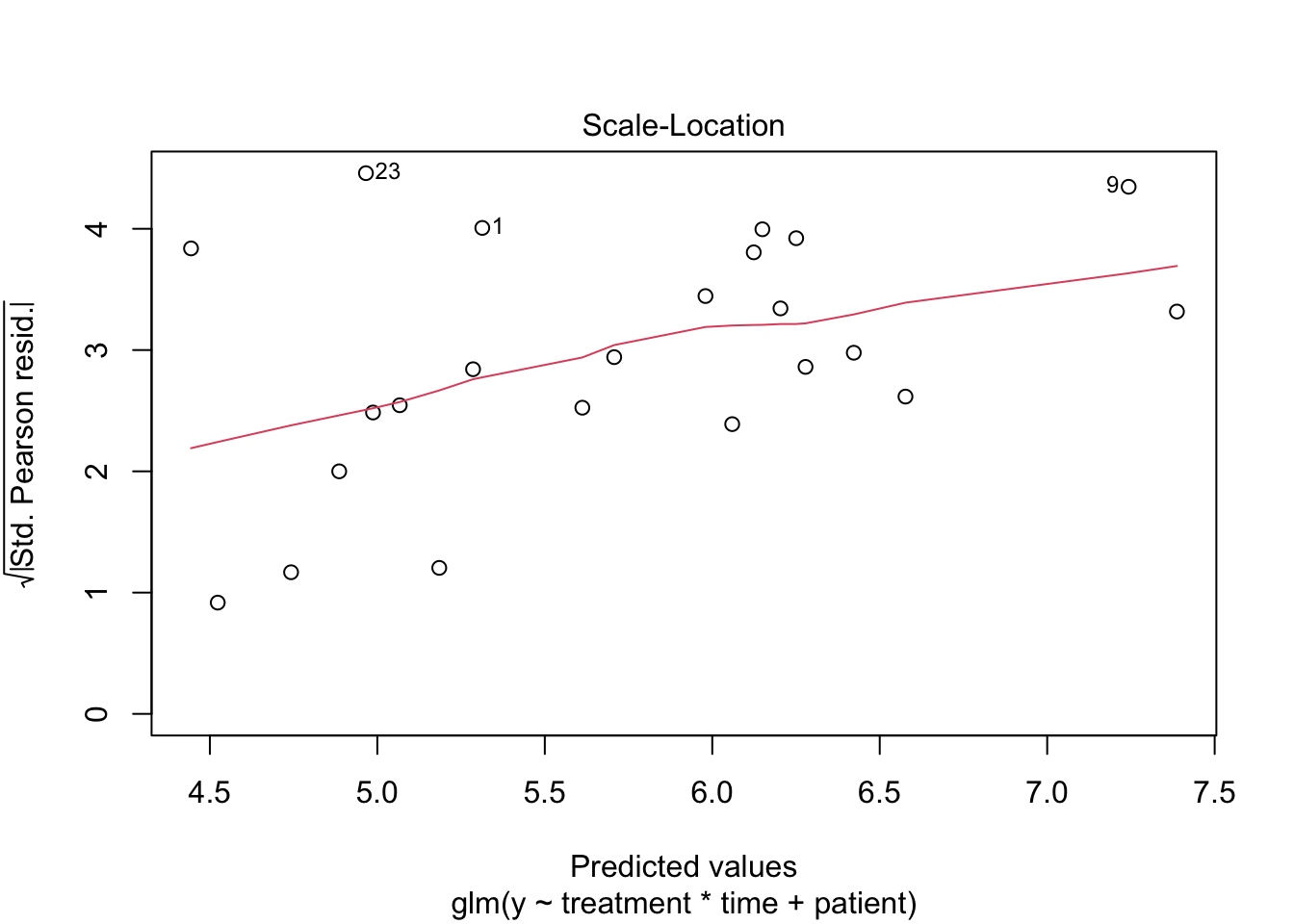
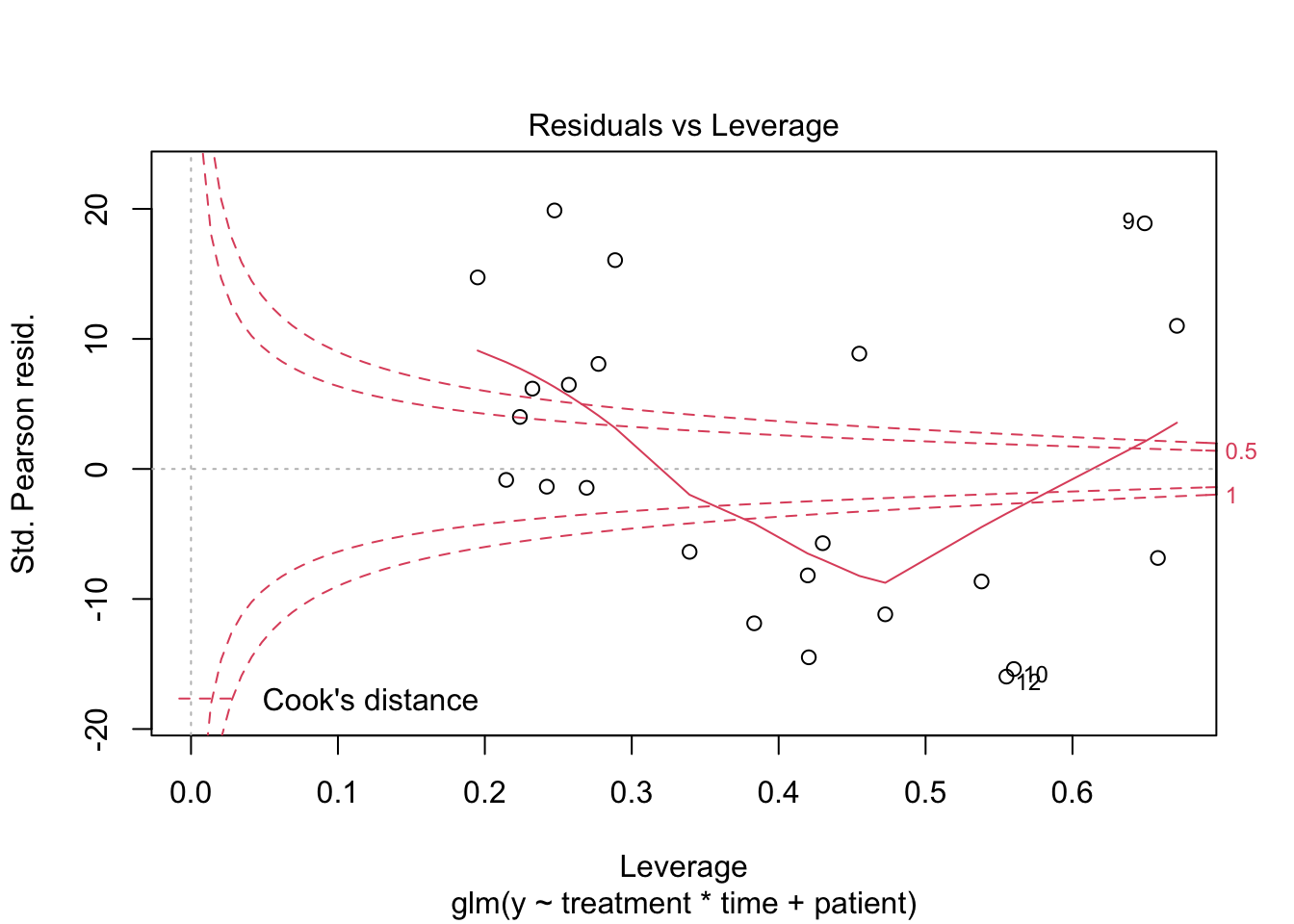
2 Negative binomial model

library(MASS)
mNB <- glm.nb(y ~ treatment*time + patient)
plot(mNB)

summary(mNB)

## 
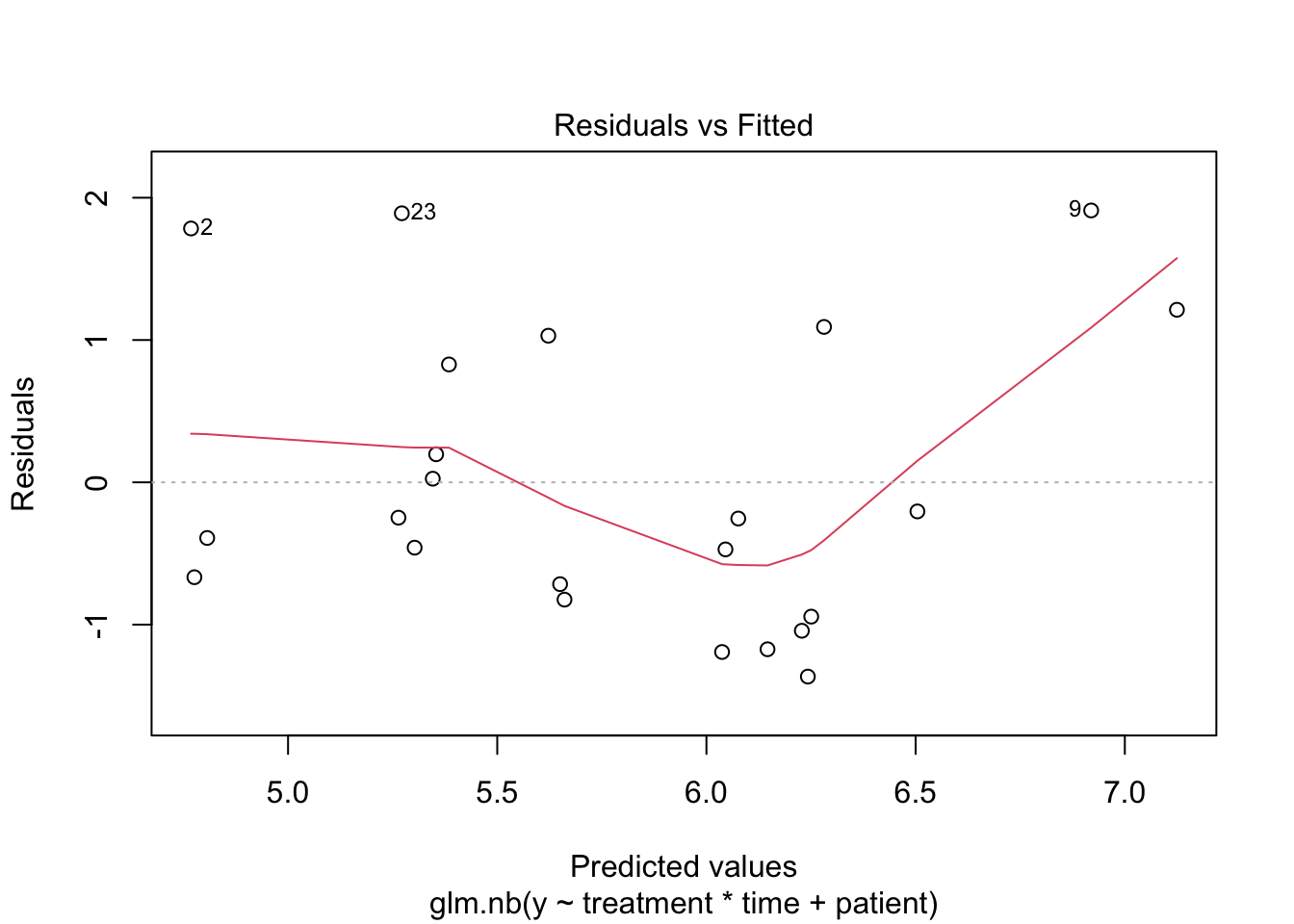
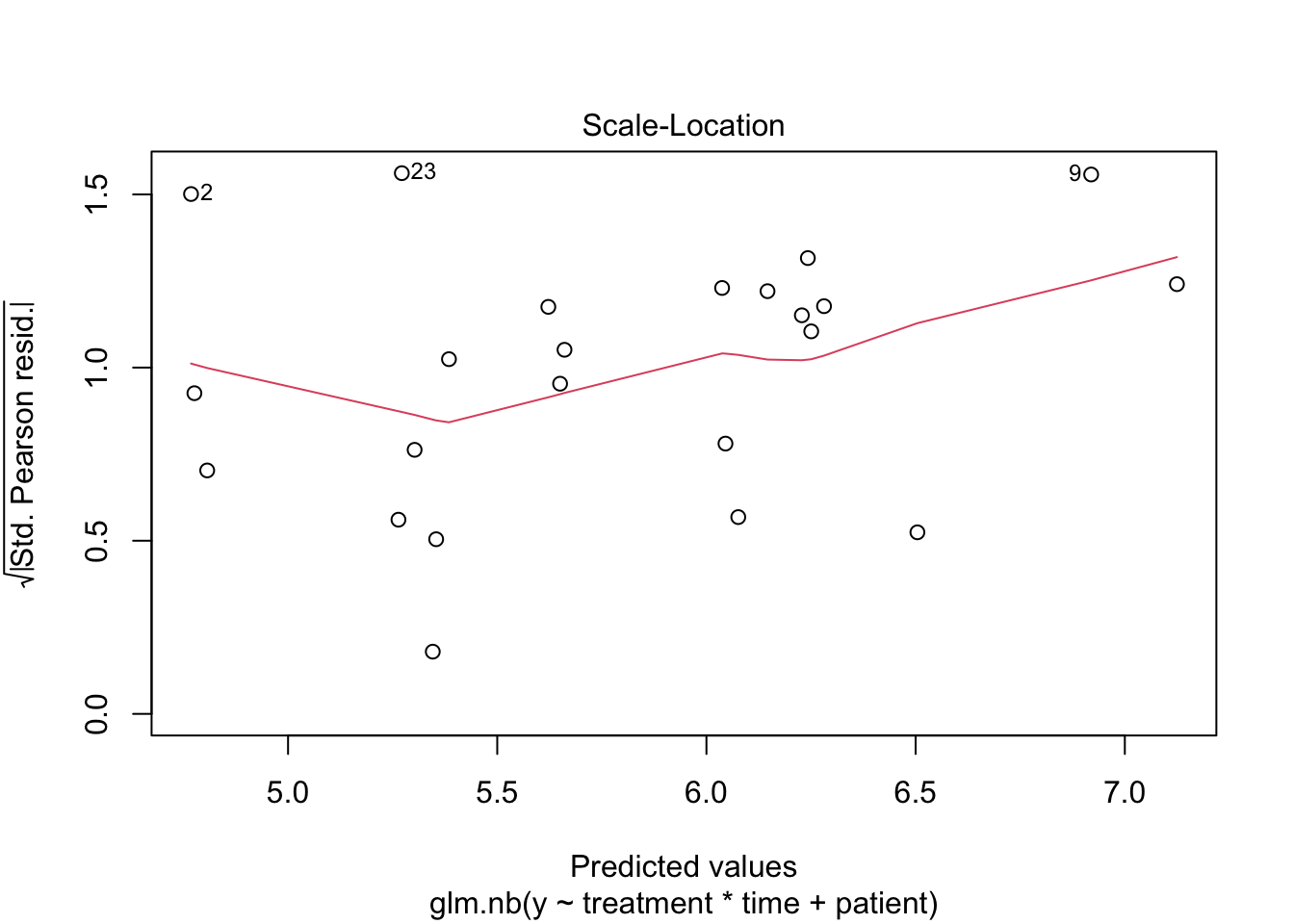
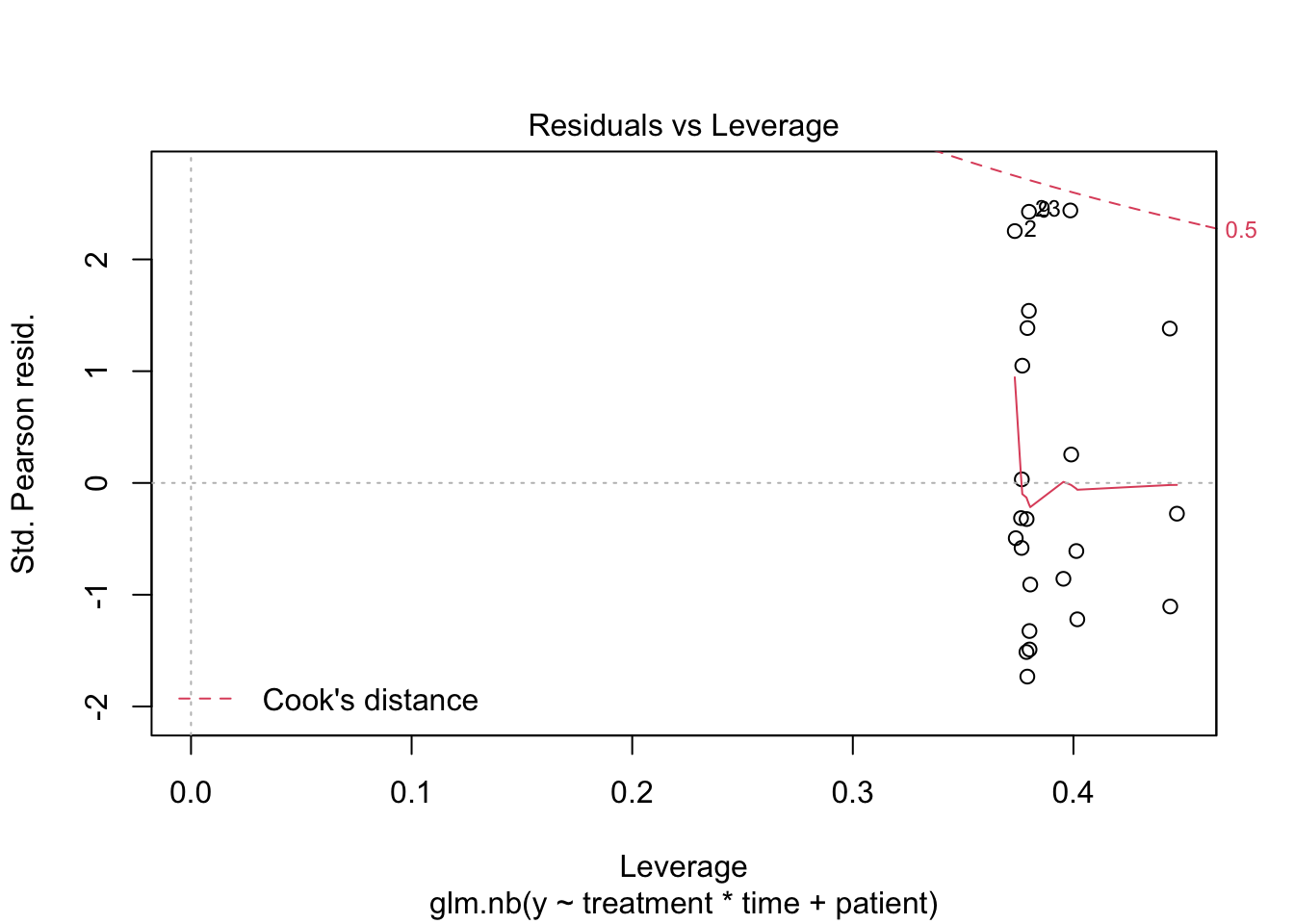
## Call:
## glm.nb(formula = y ~ treatment * time + patient, init.theta = 5.797944761, 
##     link = log)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.7692  -0.8726  -0.2641   0.8303   1.5579  
## 
## Coefficients:
##                       Estimate Std. Error z value Pr(>|z|)    
## (Intercept)           5.622089   0.279514  20.114  < 2e-16 ***
## treatmentDPN          0.415319   0.324036   1.282 0.199945    
## treatmentOHT          0.620294   0.323896   1.915 0.055479 .  
## time48h              -0.854023   0.325959  -2.620 0.008792 ** 
## patient2              0.882139   0.241916   3.646 0.000266 ***
## patient3              0.038663   0.242737   0.159 0.873450    
## patient4              0.008082   0.258521   0.031 0.975059    
## treatmentDPN:time48h  0.162526   0.440457   0.369 0.712132    
## treatmentOHT:time48h -0.124510   0.440453  -0.283 0.777417    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(5.7979) family taken to be 1)
## 
##     Null deviance: 90.709  on 22  degrees of freedom
## Residual deviance: 23.560  on 14  degrees of freedom
## AIC: 308.63
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  5.80 
##           Std. Err.:  1.69 
## 
##  2 x log-likelihood:  -288.632

2.1 Statistical inference

We will test seven different contrasts.

L <- matrix(0, nrow = length(coef(mNB)), ncol = 7)
rownames(L) <- names(coef(mNB))
colnames(L) <- c("DPNvsCON24", "DPNvsCON48",
                 "OHTvsCON24", "OHTvsCON48",
                 "DPNvsCONInt", "OHTvsCONInt",
                 "OHTvsDPNInt")
# DPN vs control at 24h
L[2,"DPNvsCON24"] <- 1
# DPN vs control at 48h
L[c(2,8),"DPNvsCON48"] <- 1
# OHT vs control at 24h
L[3,"OHTvsCON24"] <- 1
# OHT vs control at 48h
L[c(3,9),"OHTvsCON48"] <- 1
# DPN control interaction
L[8,"DPNvsCONInt"] <- 1
# OHT control interaction
L[9,"OHTvsCONInt"] <- 1
# OHT DPN interaction
L[c(9,8),"OHTvsDPNInt"] <- c(1, -1)

L

##                      DPNvsCON24 DPNvsCON48 OHTvsCON24 OHTvsCON48 DPNvsCONInt
## (Intercept)                   0          0          0          0           0
## treatmentDPN                  1          1          0          0           0
## treatmentOHT                  0          0          1          1           0
## time48h                       0          0          0          0           0
## patient2                      0          0          0          0           0
## patient3                      0          0          0          0           0
## patient4                      0          0          0          0           0
## treatmentDPN:time48h          0          1          0          0           1
## treatmentOHT:time48h          0          0          0          1           0
##                      OHTvsCONInt OHTvsDPNInt
## (Intercept)                    0           0
## treatmentDPN                   0           0
## treatmentOHT                   0           0
## time48h                        0           0
## patient2                       0           0
## patient3                       0           0
## patient4                       0           0
## treatmentDPN:time48h           0          -1
## treatmentOHT:time48h           1           1

2.1.1 Wald test

beta <- matrix(coef(mNB), ncol = 1)
waldStats <- c()
for(ll in 1:ncol(L)){
  curL <- L[,ll,drop=FALSE]
  curWald <- t(curL) %*% beta %*% solve(t(curL) %*% vcov(mNB) %*% curL) %*% t(beta) %*% curL
  waldStats[ll] <- curWald
}

waldStats

## [1] 1.64277658 3.75083592 3.66762230 2.75849551 0.13615681 0.07991173 0.46952521

pvalues <- 1-pchisq(waldStats, df=1)
pvalues

## [1] 0.19994494 0.05278111 0.05547928 0.09673917 0.71213195 0.77741707 0.49320567

2.1.2 Likelihood ratio test

Implementing these contrasts using a likelihood ratio test is possible, but is not trivial. It would require a reparameterization of our model using the contrasts of interest. In this reparameterization, one variable may correspond to one contrast. We may then compare a full to an alternative model, dropping this variable, using a likelihood ratio test. While it is important to know that this is possible, we will not implement the reparameterization ourselves as it is considered outside the scope of this course.

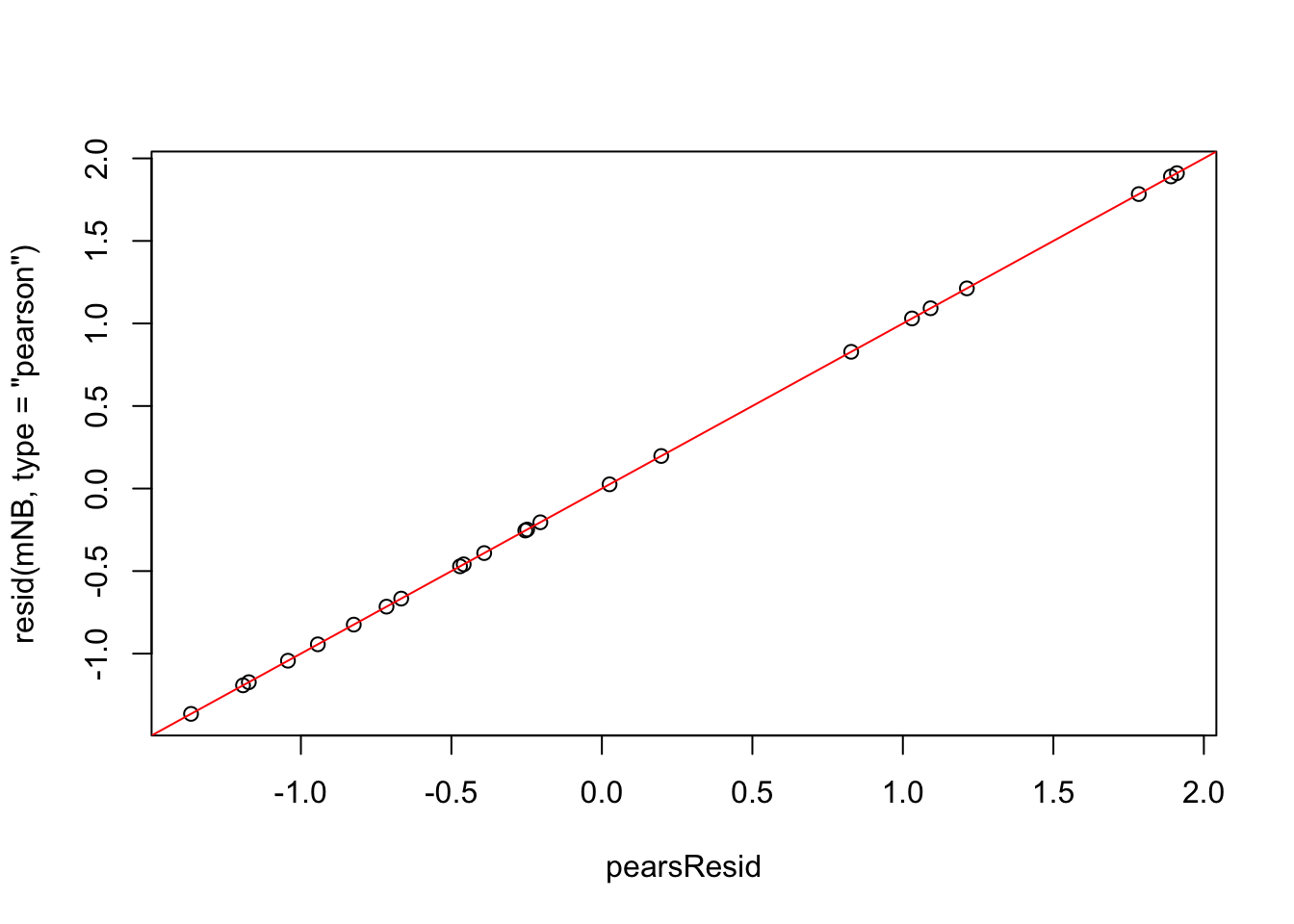
3 Residuals

3.1 Deviance residuals

## residual deviance
sum(2*(dnbinom(x=y, mu=y, size=mNB$theta, log=TRUE) - dnbinom(x=y, mu=fitted(mNB), size=mNB$theta, log=TRUE)))

## [1] 23.5601

## deviance residual
devResid <- sign(y-fitted(mNB)) * sqrt(2*(dnbinom(x=y, mu=y, size=mNB$theta, log=TRUE) - 
                      dnbinom(x=y, mu=fitted(mNB), size=mNB$theta, log=TRUE)))

range(devResid - resid(mNB, type="deviance"))

## [1] -8.070651e-10  9.068435e-10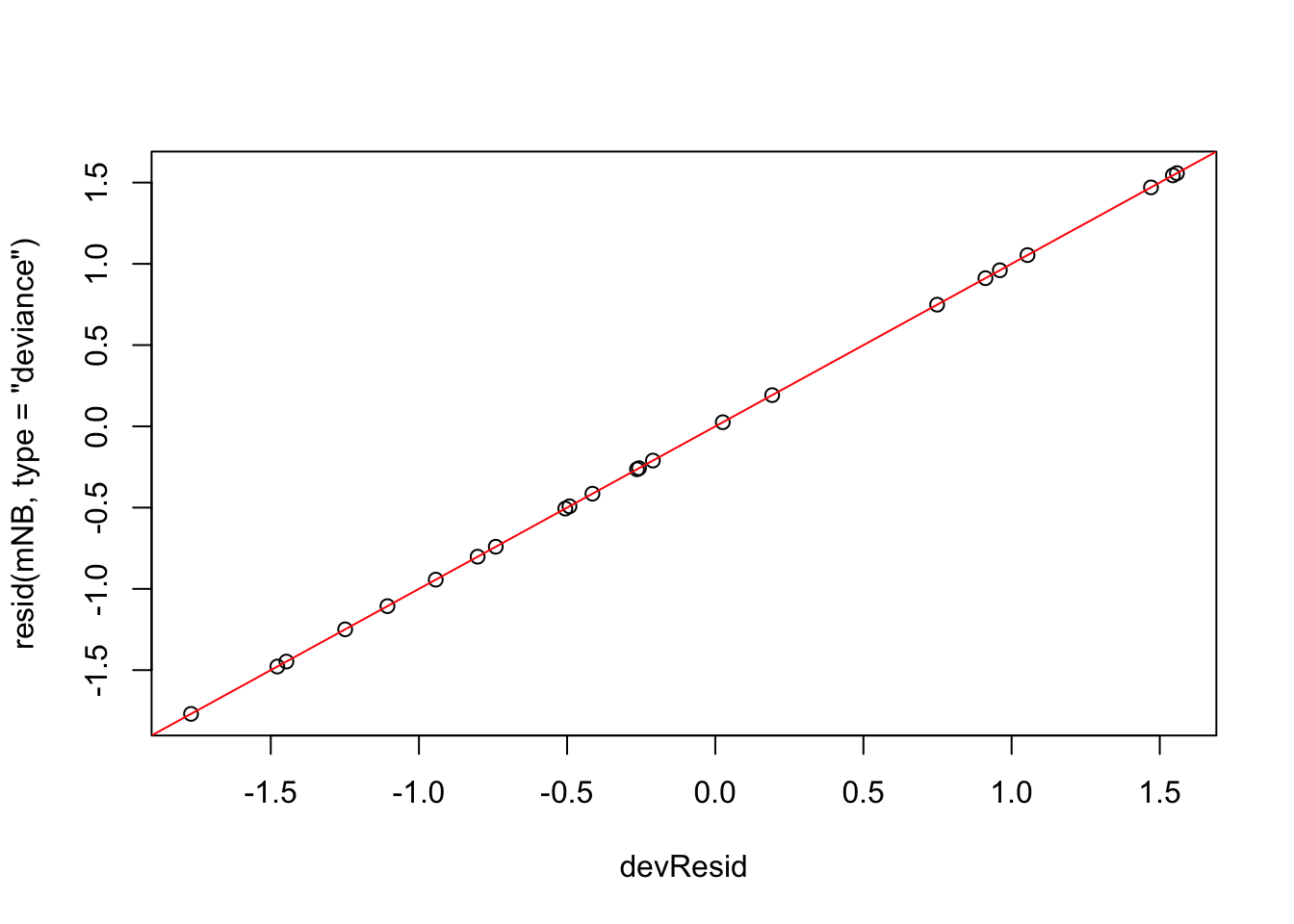

plot(devResid, resid(mNB, type="deviance")) ; abline(0,1, col="red")

3.2 Pearson residuals

pearsResid <- (y - fitted(mNB)) / sqrt(fitted(mNB) + 1/mNB$theta * fitted(mNB)^2)
range(pearsResid - resid(mNB, type="pearson"))

## [1] -9.888568e-10  7.026788e-10

plot(x=pearsResid, y=resid(mNB, type="pearson")) ; abline(0,1, col="red")

3.3 Goodness-of-fit

X2 <- sum(pearsResid^2)
1-pchisq(X2, df=length(y) - length(coef(mNB)))

## [1] 0.04729423

4 Re-analysis upon basic normalization

A very simple normalization would use an offset to account for sequencing depth. Verify if our hypothesis test results remain upon using this basic normalization.

seqDepth <- colSums(assays(se)$counts)

4.1 Statistical inference

5 Negative binomial model, corrected for sequencing depth

library(MASS)
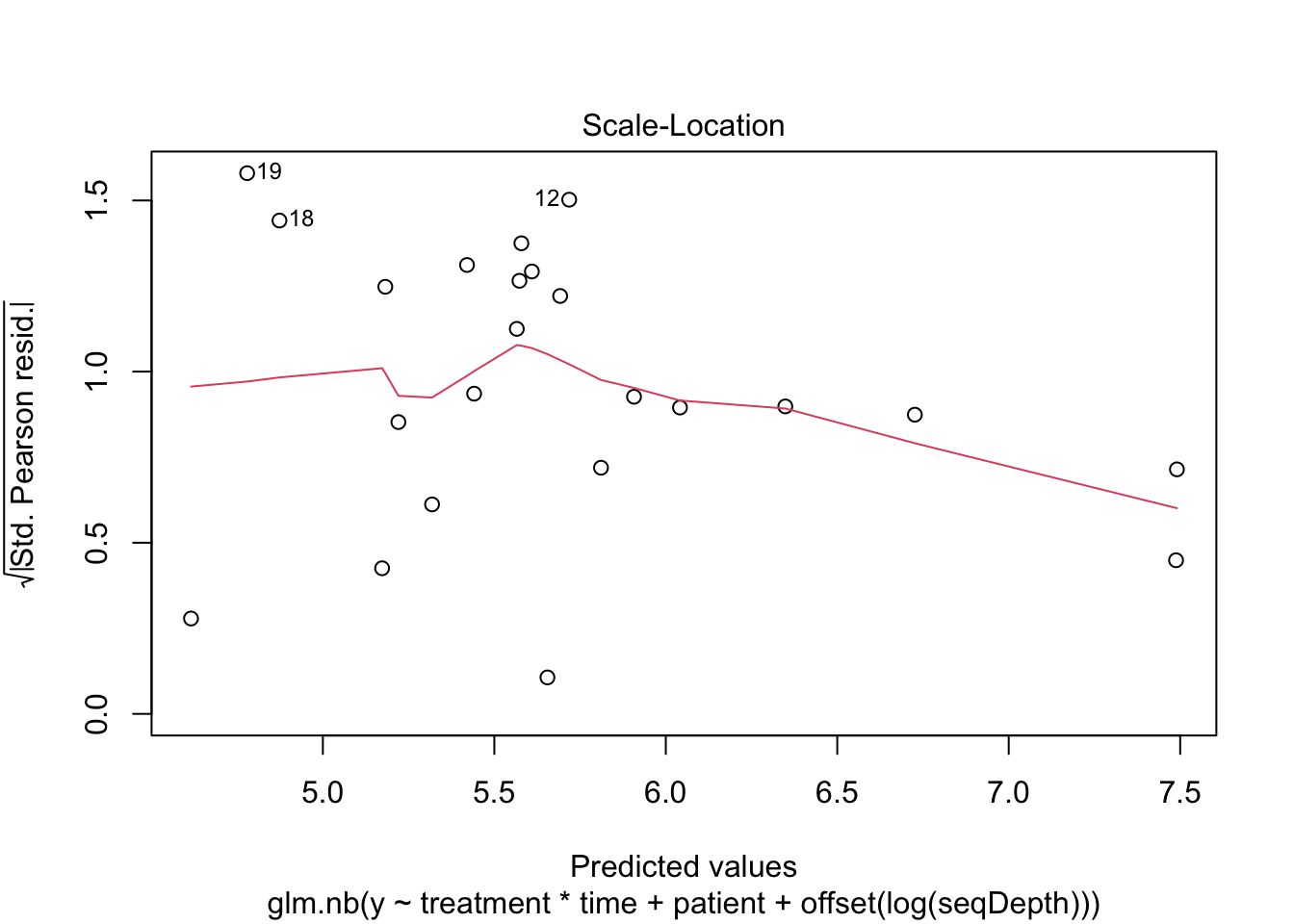
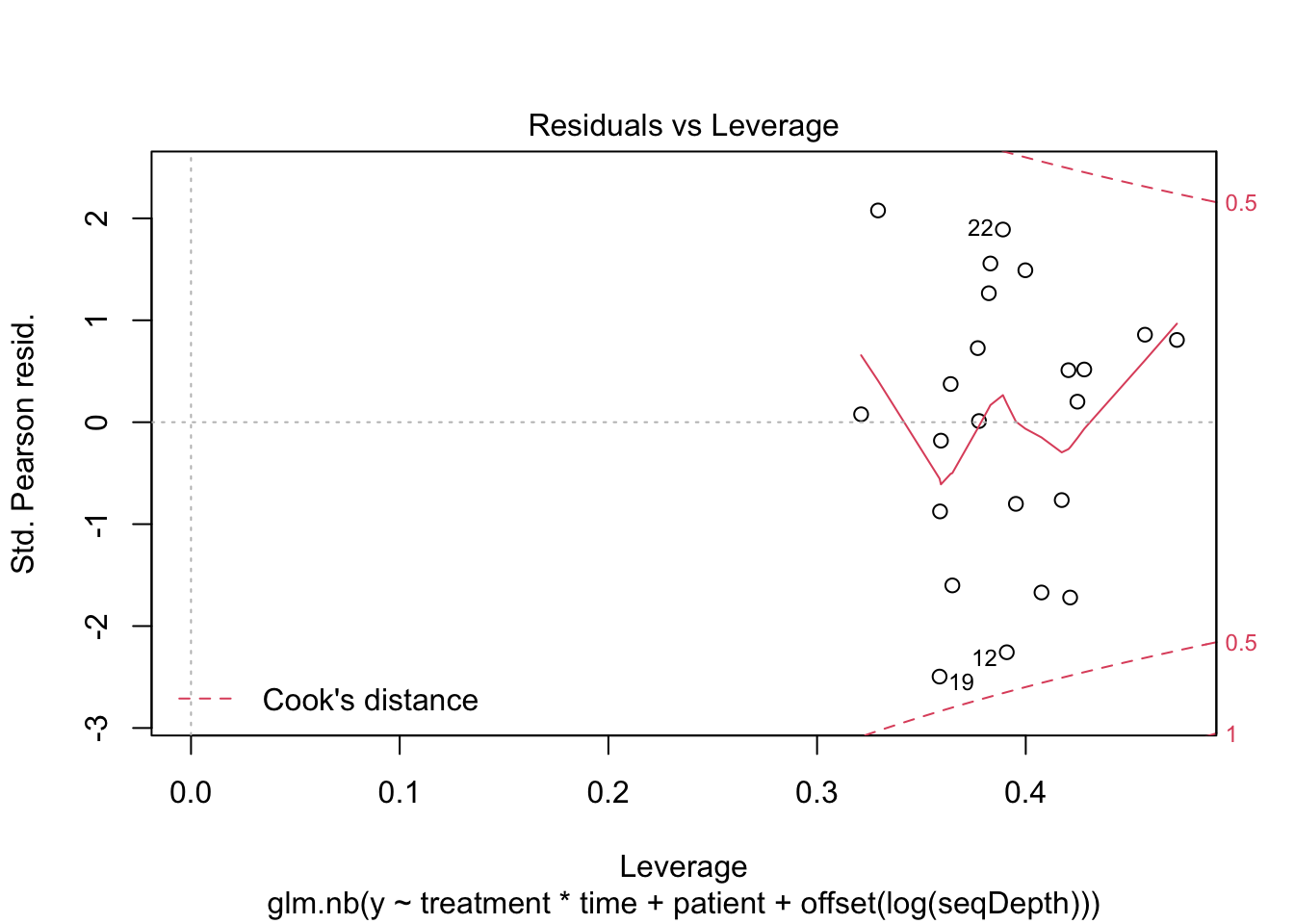
mNBOffset <- glm.nb(y ~ treatment*time + patient +
                offset(log(seqDepth)))
plot(mNBOffset)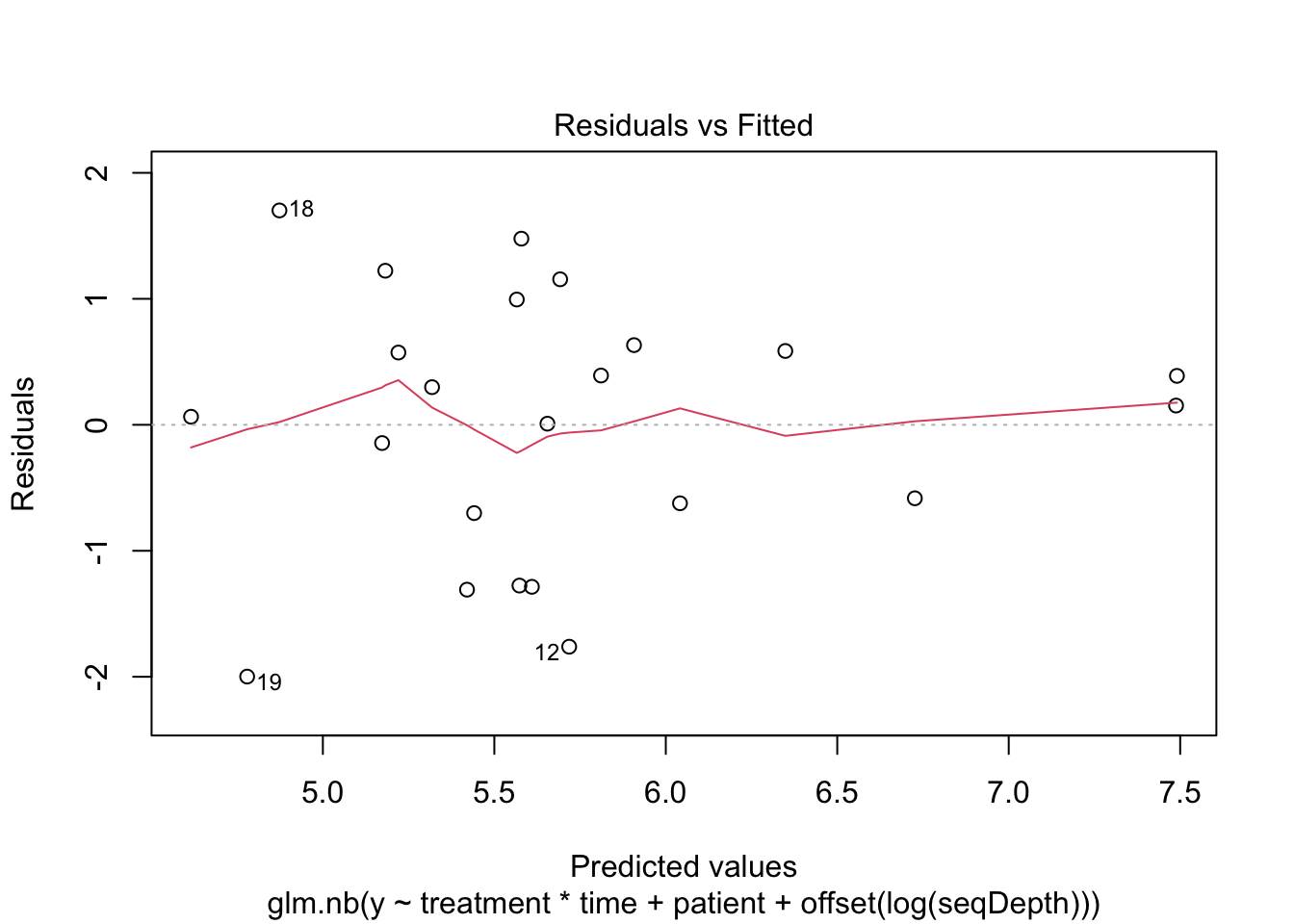

summary(mNBOffset)

## 
## Call:
## glm.nb(formula = y ~ treatment * time + patient + offset(log(seqDepth)), 
##     init.theta = 82.98036979, link = log)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.1746  -0.6788   0.1520   0.5961   1.6033  
## 
## Coefficients:
##                       Estimate Std. Error  z value Pr(>|z|)    
## (Intercept)          -10.11672    0.08217 -123.120  < 2e-16 ***
## treatmentDPN           0.09023    0.09418    0.958 0.338022    
## treatmentOHT           0.13403    0.09362    1.432 0.152224    
## time48h               -0.89874    0.10008   -8.980  < 2e-16 ***
## patient2               0.49680    0.07174    6.925 4.37e-12 ***
## patient3              -0.27195    0.07419   -3.666 0.000247 ***
## patient4              -0.06219    0.07888   -0.788 0.430428    
## treatmentDPN:time48h   0.15540    0.13277    1.170 0.241820    
## treatmentOHT:time48h   0.17758    0.13292    1.336 0.181560    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(82.9804) family taken to be 1)
## 
##     Null deviance: 422.284  on 22  degrees of freedom
## Residual deviance:  24.637  on 14  degrees of freedom
## AIC: 253.94
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  83.0 
##           Std. Err.:  34.2 
## 
##  2 x log-likelihood:  -233.939

5.1 Wald tests

betaOffset <- matrix(coef(mNBOffset), ncol = 1)
waldStatsOffset <- c()
for(ll in 1:ncol(L)){
  curL <- L[,ll,drop=FALSE]
  curWald <- t(curL) %*% betaOffset %*% solve(t(curL) %*% vcov(mNBOffset) %*% curL) %*% t(betaOffset) %*% curL
  waldStatsOffset[ll] <- curWald
}

waldStatsOffset

## [1]  0.91792044  6.84868664  2.04982086 10.79379449  1.36995308  1.78481023
## [7]  0.03194304

pvaluesOffset <- 1-pchisq(waldStatsOffset, df=1)
pvaluesOffset

## [1] 0.338021590 0.008870646 0.152224100 0.001018409 0.241819946 0.181559766
## [7] 0.858152733