library("msqrob2")
library("ggplot2")
library("patchwork")
library("ggrepel")
library("dplyr")6 Heart use case: a MaxQuant LFQ DDA dataset with a more complex design
6.1 Introduction
In this chapter we show how to analyse LFQ data from an experiment with a more complex design. The data are a small subset of the public dataset PXD006675 on PRIDE.
Particularly, the proteomes of the atrium and ventriculum in the left and the right heart region are profiled for 3 patients (identifiers 3, 4, and 8). Hence, the design consists of a factor tissue (atrium, ventriculum), region (left, right) and block (patient 3,4, and 8).
Suppose that researchers are mainly interested in comparing the ventricular to the atrial proteome. Particularly, they would like to compare the left atrium to the left ventricle, the right atrium to the right ventricle, the average ventricular vs atrial proteome and if ventricular vs atrial proteome shifts differ between left and right heart region.
6.2 Load packages
First, we load the msqrob2 package and additional packages for data manipulation and visualisation.
We also configure the parallelisation framework.
library("BiocParallel")
register(SerialParam())6.3 Load Data
6.3.1 Getting the data
The data were searched with MaxQuant version version 1.5.5.6 and are deposited on the PRIDE repository PXD006675.
In this chapter we use a small subset of the data that is available on TODO put on Zenodo and use BiocFileCache.
library("BiocFileCache")
bfc <- BiocFileCache()
pepFile <- bfcrpath(bfc, "https://raw.githubusercontent.com/statOmics/PDA21/data/quantification/heart/peptides.txt")After downloading the files, we can load the peptide table, which is in “wide format”. Hence, each row represents a single peptide and that each quantification column (that starts with "Intensity") represents a single sample.
peps <- read.delim(pepFile)
quantcols <- grep("Intensity\\.", names(peps), value = TRUE)| Sequence | N.term.cleavage.window | C.term.cleavage.window | Amino.acid.before | First.amino.acid | Second.amino.acid | Second.last.amino.acid | Last.amino.acid | Amino.acid.after | A.Count | R.Count | N.Count | D.Count | C.Count | Q.Count | E.Count | G.Count | H.Count | I.Count | L.Count | K.Count | M.Count | F.Count | P.Count | S.Count | T.Count | W.Count | Y.Count | V.Count | U.Count | O.Count | Length | Missed.cleavages | Mass | Proteins | Leading.razor.protein | Start.position | End.position | Gene.names | Protein.names | Unique..Groups. | Unique..Proteins. | Charges | PEP | Score | Identification.type.LA3 | Identification.type.LA4 | Identification.type.LA8 | Identification.type.LV3 | Identification.type.LV4 | Identification.type.LV8 | Identification.type.RA3 | Identification.type.RA4 | Identification.type.RA8 | Identification.type.RV3 | Identification.type.RV4 | Identification.type.RV8 | Fraction.Average | Fraction.Std..Dev. | Fraction.1 | Fraction.2 | Fraction.3 | Fraction.4 | Fraction.5 | Fraction.6 | Fraction.7 | Fraction.8 | Fraction.100 | Experiment.LA3 | Experiment.LA4 | Experiment.LA8 | Experiment.LV3 | Experiment.LV4 | Experiment.LV8 | Experiment.RA3 | Experiment.RA4 | Experiment.RA8 | Experiment.RV3 | Experiment.RV4 | Experiment.RV8 | Intensity | Intensity.LA3 | Intensity.LA4 | Intensity.LA8 | Intensity.LV3 | Intensity.LV4 | Intensity.LV8 | Intensity.RA3 | Intensity.RA4 | Intensity.RA8 | Intensity.RV3 | Intensity.RV4 | Intensity.RV8 | Reverse | Potential.contaminant | id | Protein.group.IDs | Mod..peptide.IDs | Evidence.IDs | MS.MS.IDs | Best.MS.MS | Oxidation..M..site.IDs | MS.MS.Count |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AAAAAAAAAK | AKFRKQERAAAAAAAA | AAAAAAAKNGSSGKKS | R | A | A | A | K | N | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 785.4396 | Q99453 | Q99453 | 159 | 168 | PHOX2B | Paired mesoderm homeobox protein 2B | yes | yes | 2 | 0.0000121 | 170.060 | By matching | By matching | By matching | By matching | By matching | By matching | By matching | By matching | 83.5 | 35.9 | NA | 2 | 1 | 5 | 1 | 7 | 2 | 6 | 113 | 1 | 1 | NA | 1 | 1 | NA | NA | 1 | 1 | 1 | 1 | NA | 3.4832e+10 | 288590000 | 118170000 | 0 | 257550000 | 308710000 | 0 | 0 | 194640000 | 144740000 | 456330000 | 107900000 | 0 | NA | 1 | 9885 | 1 | 9;10;11;12;13;14;15;16;17;18;19;20;21;22;23;24;25;26;27;28;29;30;31;32;33;34;35;36;37;38;39;40;41;42;43;44;45;46;47;48;49;50;51;52;53;54;55;56;57;58;59;60;61;62;63;64;65;66;67;68;69;70;71;72;73;74;75;76;77;78;79;80;81;82;83;84;85;86;87;88;89;90;91;92;93;94;95;96;97;98;99;100;101;102;103;104;105;106;107;108;109;110;111;112;113;114;115;116;117;118;119;120;121;122;123;124;125;126;127;128;129;130;131;132;133;134;135;136;137;138;139;140;141;142;143;144;145 | 9;10;11;12;13;14;15;16;17;18;19;20;21;22;23;24;25;26;27;28;29;30;31;32;33;34;35;36;37;38;39;40;41;42;43;44;45;46;47;48;49;50;51;52;53;54;55;56;57;58;59;60;61;62 | 18 | 50 | ||||||
| AAAAAAAAEQQSSNGPVK | ________________ | QSSNGPVKKSMREKAV | M | A | A | V | K | K | 8 | 0 | 1 | 0 | 0 | 2 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 18 | 0 | 1640.8118 | Q16585 | Q16585 | 2 | 19 | SGCB | Beta-sarcoglycan | yes | yes | 2 | 0.0000000 | 185.250 | By MS/MS | By MS/MS | 4.5 | 1.8 | NA | 2 | NA | NA | 1 | 3 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | 1 | 1 | NA | 9.4024e+07 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 29925000 | 0 | NA | 4 | 7001 | 4;5 | 149;150;151;152;153;154 | 67;68;69;70;71;72;73 | 67 | 7 | ||||||||||||
| AAAAAAAAGAFAGR | APLLGARRAAAAAAAA | AAGAFAGRRAACGAVL | R | A | A | G | R | R | 10 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 0 | 1145.5942 | Q8N697 | Q8N697 | 20 | 33 | SLC15A4 | Solute carrier family 15 member 4 | yes | yes | 2 | 0.0003300 | 119.620 | 7.0 | 0.0 | NA | NA | NA | NA | NA | NA | 5 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | 2.5454e+08 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | NA | 5 | 8631 | 6 | 155;156;157;158;159 | 74;75 | 74 | 1 | ||||||||||||||
| AAAAAAAPEPPLGLQQLSALQPEPGGVPLHSSWTFWLDR | AREPPGSRAAAAAAAP | SWTFWLDRSLPGATAA | R | A | A | D | R | S | 8 | 1 | 0 | 1 | 0 | 3 | 2 | 3 | 1 | 0 | 6 | 0 | 0 | 1 | 6 | 3 | 1 | 2 | 0 | 1 | 0 | 0 | 39 | 0 | 4049.0799 | Q8N5X7 | Q8N5X7 | 21 | 59 | EIF4E3 | Eukaryotic translation initiation factor 4E type 3 | yes | yes | 3;4 | 0.0000700 | 57.832 | By matching | By MS/MS | 2.5 | 1.5 | 1 | 2 | NA | NA | 1 | NA | NA | NA | NA | 1 | NA | NA | NA | NA | NA | 1 | NA | NA | NA | NA | NA | 8.5505e+07 | 15932000 | 0 | 0 | 0 | 0 | 0 | 8996400 | 0 | 0 | 0 | 0 | 0 | NA | 9 | 8622 | 10 | 601;602;603;604 | 349;350;351 | 349 | 3 | ||||||||||||
| AAAAAAGAASGLPGPVAQGLK | ________________ | GPVAQGLKEALVDTLT | M | A | A | L | K | E | 9 | 0 | 0 | 0 | 0 | 1 | 0 | 4 | 0 | 0 | 2 | 1 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 21 | 0 | 1747.9581 | Q96P70 | Q96P70 | 2 | 22 | IPO9 | Importin-9 | yes | yes | 2 | 0.0000001 | 177.810 | 1.0 | 0.0 | 1 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | 3.3872e+07 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | NA | 12 | 9760 | 13 | 686 | 450 | 450 | 1 | ||||||||||||||
| AAAAAATAPPSPGPAQPGPR | AAPARAPRAAAAAATA | GPAQPGPRAQRAAPLA | R | A | A | P | R | A | 8 | 1 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | 1754.9064 | Q6SPF0 | Q6SPF0 | 151 | 170 | SAMD1 | Atherin | yes | yes | 2 | 0.0007018 | 72.290 | 7.0 | 0.0 | NA | NA | NA | NA | NA | NA | 1 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA | 9.4351e+06 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | NA | 16 | 7795 | 18 | 720 | 472 | 472 | 1 |
We now extract the sample annotations. We will build a table where each row in the annotation table contains information for one sample (the table below shows the first 6 rows). This information is extracted from the sample names.
coldata <- data.frame(quantCols = quantcols) |>
mutate(location = substr(quantCols, 11, 11)) |> # heart region left-right
mutate(tissue = substr(quantCols, 12, 12)) |> # tissue Atrium-Ventriculum
mutate(patient = substr(quantCols, 13, 13)) # patient id| quantCols | location | tissue | patient |
|---|---|---|---|
| Intensity.LA3 | L | A | 3 |
| Intensity.LA4 | L | A | 4 |
| Intensity.LA8 | L | A | 8 |
| Intensity.LV3 | L | V | 3 |
| Intensity.LV4 | L | V | 4 |
| Intensity.LV8 | L | V | 8 |
6.3.2 The QFeatures data class
We combine the two tables into a QFeatures object.
(pe <- readQFeatures(
peps, colData = coldata, fnames = "Sequence", name = "peptides"
))An instance of class QFeatures (type: bulk) with 1 set:
[1] peptides: SummarizedExperiment with 31319 rows and 12 columns We now have a QFeatures object with 1 set, containing r nrows(pe)[[1]] rows (peptides) and 12 columns (samples).
6.4 Data preprocessing
msqrob2 relies on the QFeatures data structure, meaning that we can directly make use of QFeatures’ data preprocessing functionality (see also the QFeatures documentation).
6.4.1 Encoding missing values
Peptides with zero intensities should be encoded using NA.
pe <- zeroIsNA(pe, "peptides")We calculate how many non zero intensities we have per peptide and this is often useful for filtering.
naResults <- nNA(pe, "peptides")
data.frame(naResults$nNArows) |>
ggplot() +
aes(x = nNA) +
geom_histogram()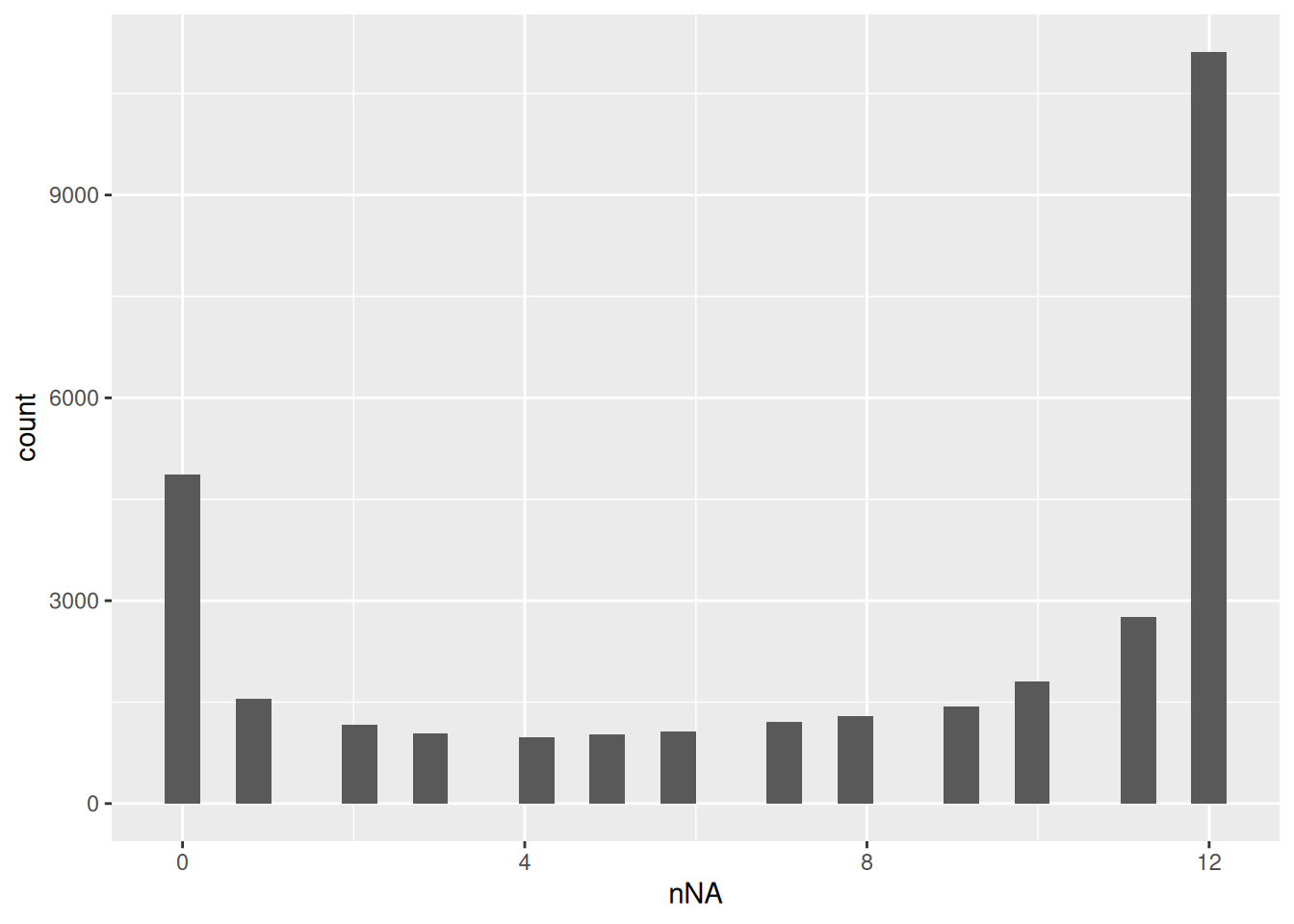
6.4.2 PSM filtering
We filter features based on 3 criteria (see PSM filtering).
- Remove failed protein inference
We remove peptides that could not be uniquely mapped to a protein.
pe <- filterFeatures(pe,
~ Proteins != "" & ## Remove failed protein inference
!grepl(";", Proteins)) ## Remove protein groups- Remove reverse sequences (decoys) and contaminants
We remove the contaminants and peptides that map to decoy sequences. These features bear no information of interest and will reduce the statistical power upon multiple test adjustment.
pe <- filterFeatures(pe, ~ Reverse != "+" & Potential.contaminant != "+")- Remove highly missing peptides.
We keep peptides that were observed at last 3 times out of the \(n = 12\) samples, so we tolerate the following proportion of NAs: \(\text{pNA} = \frac{(n - 3)}{n} = 0.75\), so we keep peptides that are observed in at least 25% of the samples.
nObs <- 3
n <- ncol(pe[["peptides"]])
(pe <- filterNA(pe, i = "peptides", pNA = (n - nObs) / n))An instance of class QFeatures (type: bulk) with 1 set:
[1] peptides: SummarizedExperiment with 15630 rows and 12 columns We keep 15630 peptides upon filtering.
6.4.3 Standard preprocessing workflow
We can now prepare the data for modelling. The workflow ensures the data complies to msqrob2’s requirements:
- Intensities are log-transformed.
pe <- logTransform(pe, base = 2, i = "peptides", name = "peptides_log")- Normalisation with Median of Ratios method.
pseudoRef <- assay(pe[["peptides_log"]]) |>
rowMeans(na.rm = TRUE) #1. Calculate the row means
nfLog <- sweep(
assay(pe[["peptides_log"]]),
MARGIN = 1,
pseudoRef) |> #2. Subtract the row means row-by-row (MARGIN = 1)
colMedians(na.rm = TRUE) #3. Calculate the column median
pe <-
sweep(pe,
MARGIN = 2,
STATS = nfLog ,
i = "peptides_log",
name = "peptides_norm") #4. Subtract log2 norm factor column-by-column (MARGIN = 2)Upon the normalisation the density curves should be nicely centred. To confirm this, we will plot the intensity distributions for each biorepeat (mouse). longForm() seamlessly combines the quantification and annotation data into a table suitable for ggplot2 visualisation. We also subset the object with the data before and after normalisation.
longForm(pe[, , c("peptides_log", "peptides_norm")], colvar = "patient") |>
ggplot() +
aes(x = value, group = colname, color = patient) +
geom_density() +
facet_wrap(~ assay, scale = "free")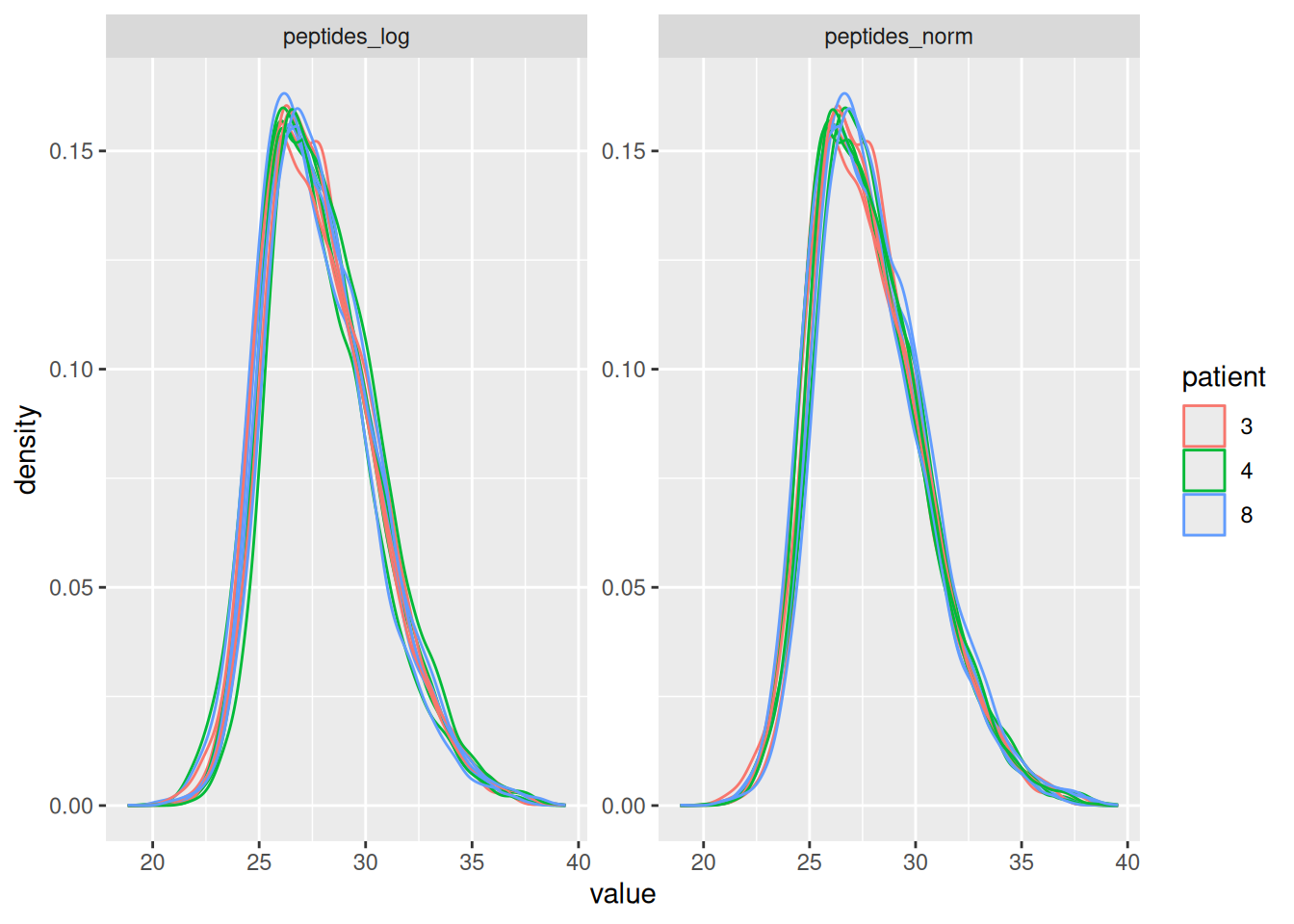
- Summarisation to protein level.
We use the robust summary approach to infer protein-level data from peptide-level data, accounting for the fact that different peptides have ionisation efficiencies hence leading to different intensity baselines.
pe <- aggregateFeatures(
pe, i = "peptides_norm", fcol = "Proteins",
fun = MsCoreUtils::medianPolish,
na.rm = TRUE, name = "proteins"
)6.5 Data exploration
We will explore the main sources of variation in the data using MDS.
library("scater")
se <- getWithColData(pe, "proteins") |>
as("SingleCellExperiment") |>
runMDS(exprs_values = 1)
plotMDS(se, colour_by = "tissue") +
plotMDS(se, colour_by = "location") +
plotMDS(se, colour_by = "patient")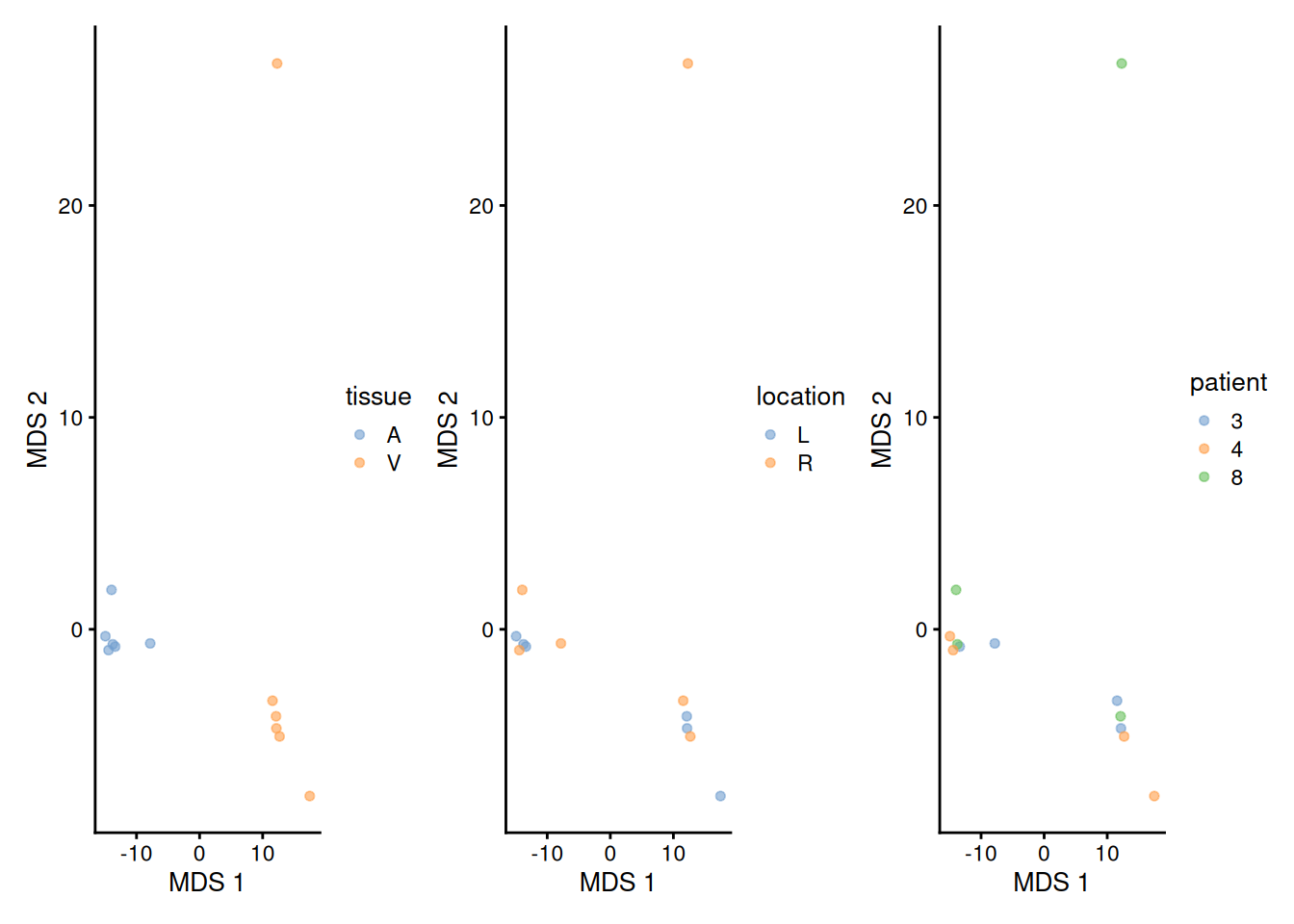
Note, that the samples upon robust summarisation show a clear separation according to the tissue type in the first dimension and according to location in the second dimension.
6.6 Data modelling
The preprocessed data can now be modelled to answer biologically relevant questions. Particularly, the protein abundance can differ according to tissue type (A-V) and location (L-R). Moreover, the effect of the tissue type can differ according to the location and vice versa. Hence, there can be an interaction between tissue and location.
The samples are also not independent as four biopsies (LA, RA, LV and RV) were taken for each patient. Because the proteome is profiled for each tissue x location combination within each patient, the design is a randomised complete block (RCB) design.
RCB designs can be correctly analysed by incorporating the block effect for patient either as a fixed or a random effect. The use of a fixed patient effect is here also possible because the effect of each factor combination can be estimated within block (patient).
Here, we choose to account for the patient effect using fixed effects because mixed models are computationally more demanding and rely on asymptotic inference (i.e. statistical inference is only valid for experiments with large sample sizes).
Now we have identified the sources of variation in the experiment that we have to account for (tissue, location and patient id), we can define a model.
model <- ~ location*tissue + ## (1) fixed effects: main effects for location and tissue type, and a tissue x location interaction
patient ## (2) fixed block effect for patient6.6.1 Estimate the model
We estimate the model with msqrob(). Recall that variables defined in model are automatically retrieved from the colData (i.e. "tissue", "location", and "patient").
pe <- msqrob(
pe, i = "proteins", formula = model, robust = TRUE, ridge = TRUE
)6.7 Statistical inference
Once the models are estimated, we can start answering biological questions by performing Statistical inference. We must translate the biological questions into a statistical hypotheses:
- Is there an effect of tissue type (V-A) in the left heart region?
- Is there an effect of tissue type (V-A) in the right heart region?
- Is there on average an effect of tissue type in the heart.
- Does the effect of tissue type (V-A) differ according to the heart region (L-R)?
In other words, we must translate these questions in a linear combination of the model parameters, also referred to as a contrast. To aid defining contrasts, we will visualise the experimental design using the ExploreModelMatrix package.
library("ExploreModelMatrix")
vd <- VisualizeDesign(
sampleData = colData(pe),
designFormula = ~ location*tissue + patient,
textSizeFitted = 4
)
vd$plotlist$`location = L`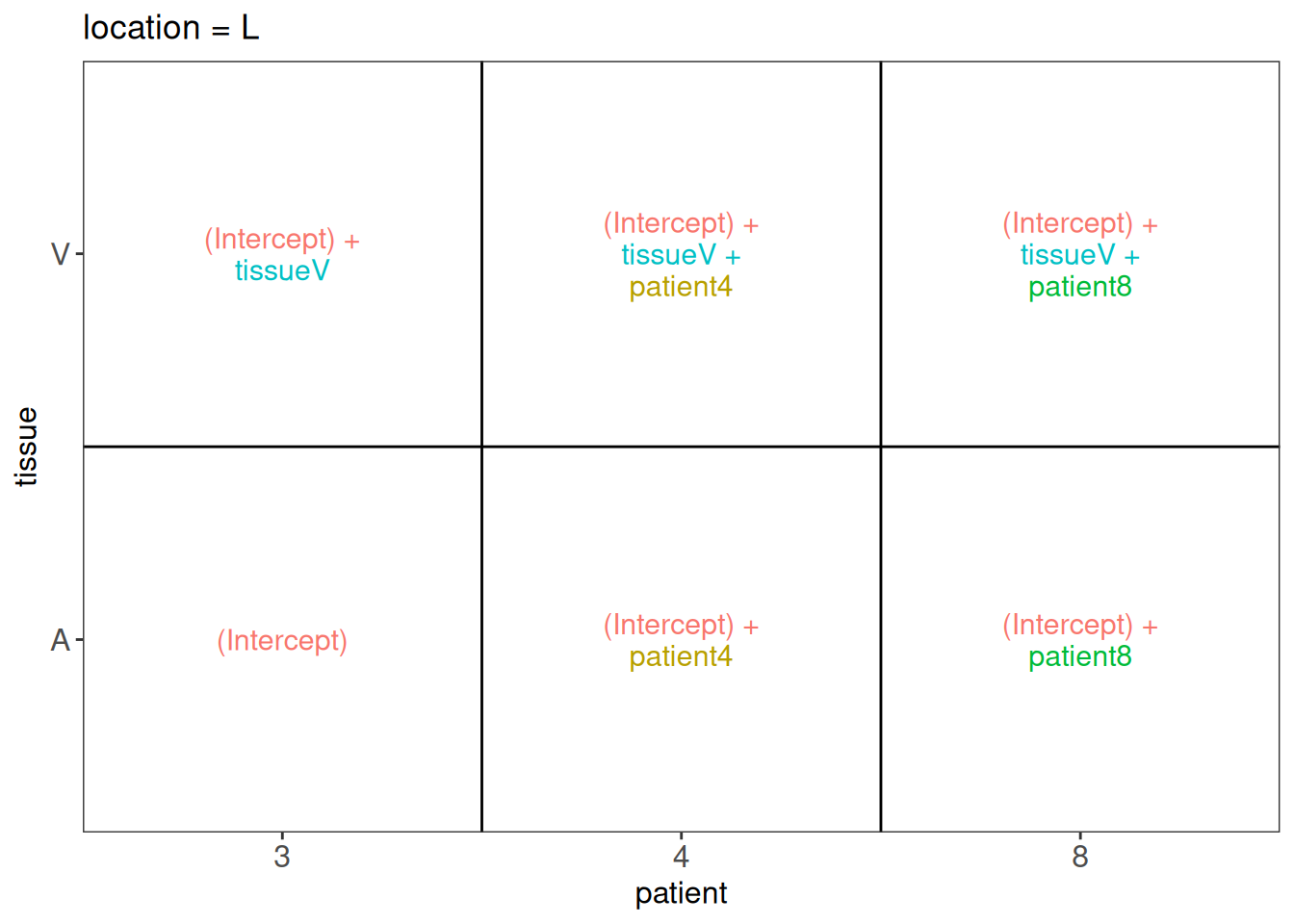
$`location = R`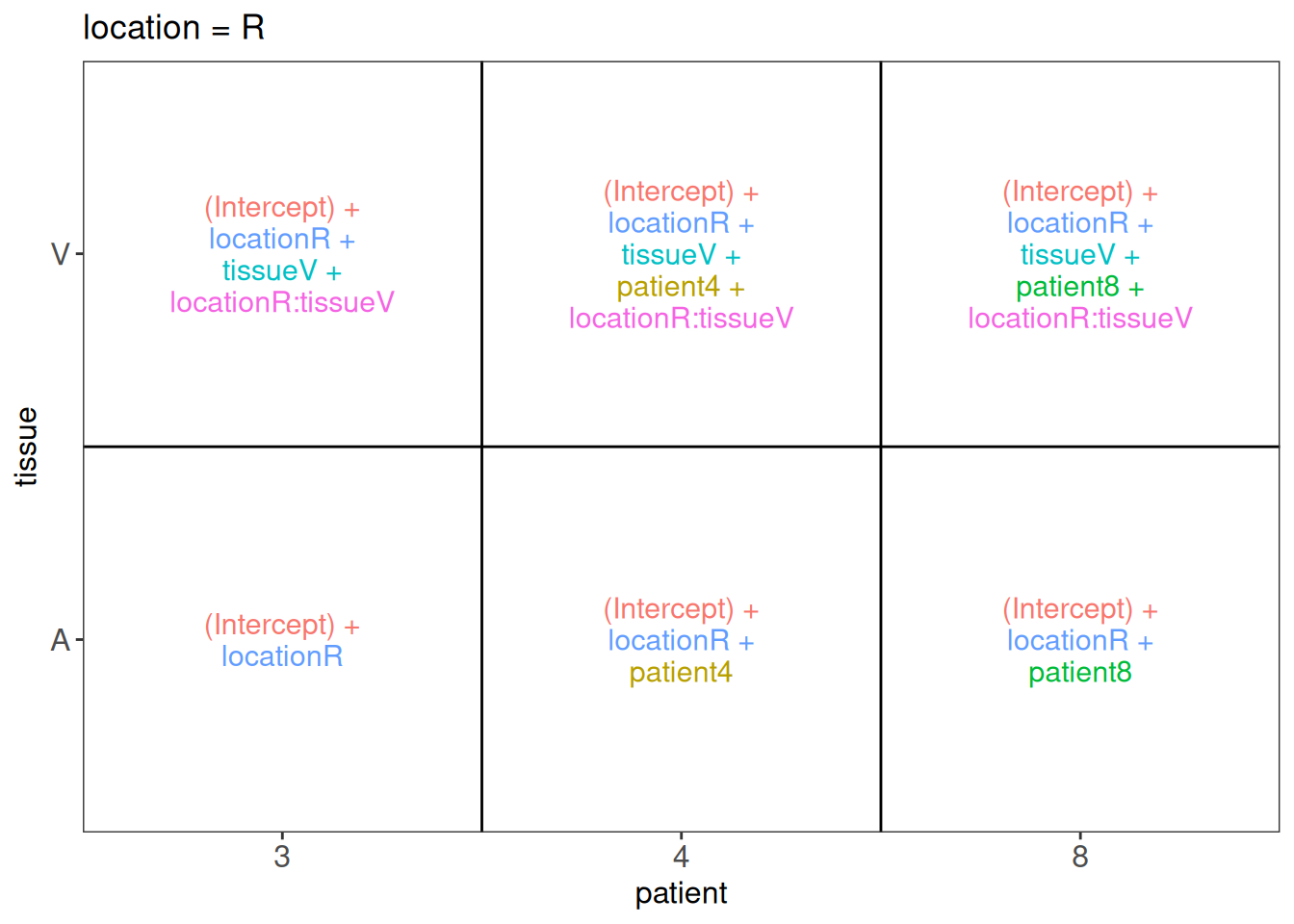
6.7.1 Research question 1: is there an effect of tissue in the left heart region?
From the plot we can see that the average log2 intensity for patient 3 in the left ventriculum equals `(Intercept) + tissueV’:
\[
\mu^L_{V,3} = \beta_0 + \beta_V
\] and for the left atrium (Intercept):
\[
\mu^L_{A,3} = \beta_0
\] So the average \(\log_2 FC\) between atrium and ventriculum for patient 3 equals to parameter tissueV
\[ \log_2 FC_{V-A}^L = \mu^L_{V,3} -\mu^L_{A,3} = \beta_V \] The same can be seen for patient 4:
\[
\log_2 FC_{V-A}^L= \mu^L_{V,4} -\mu^L_{A,4} = \beta_0 + \beta_V + \beta_4 - (\beta_0 + \beta_4) = \beta_V
\] So the parameter tissueV has the interpretation of the average \(\log_2 FC\) between ventriculum and atrium after correction for the patient effect, which quantifies the effect size for the first research hypothesis.
6.7.2 Research question 2: is there an effect of tissue in the right heart region?
When we use the same rationale for the right heart region, we can see that the average \(\log_2 FC\) between atrium and ventriculum upon correction for the patient effect equals tissueV + locationR:tissueV. So, it consists of the main effect for tissue and the location x tissue interaction.
We will illustrate this here for patient 4:
\[ \begin{array}{rcl} \log_2 FC_{V-A}^R& =&\mu^R_{V,4} -\mu^R_{A,4} \\ &=& \beta_0 + \beta_R + \beta_V + \beta_{R:V} + \beta_4 - (\beta_0 + \beta_R + \beta_4) \\ &=& \beta_V + \beta_{R:V} \end{array} \]
6.7.3 Research question 3: is there an effect of tissue on average in the heart?
This research question can be quantified by calculating the averaging the \(\log_2\) fold change between Ventriculum and Atrium over the left and right heart regions, which equals tissueV + 0.5*locationR:tissueV
\[ \begin{array}{rcl} (\log_2 FC_{V-A}^R + \log_2 FC_{V-A}^R)/ 2 &=& (\beta_V + \beta_V + \beta_{R:V})/2 \\ &=& \beta_V + 0.5\times\beta_{R:V} \end{array} \]
6.7.4 Research question 4: does the effect of tissue differs according to the heart region?
This research question can be quantified by calculating the difference in the \(\log_2\) fold change between Ventriculum and Atrium in the right and left heart regions, which equals locationR:tissueV
\[ \begin{array}{rcl} \log_2 FC_{V-A}^R- \log_2 FC_{V-A}^R &=& \beta_V + \beta_{R:V}-\beta_V \\ &=& \beta_{R:V} \end{array} \] ### Setting up the contrasts
We can set up the four contrasts:
- We make the design matrix so that we can easily extract all parameter names from the model
- We make the contrast matrix for the four contrasts
design <- model.matrix(~ location*tissue + patient, data = colData(pe))
L <- makeContrast(
c(
"ridgetissueV = 0",
"ridgetissueV + ridgelocationR:tissueV = 0",
"ridgetissueV + 0.5*ridgelocationR:tissueV = 0",
"ridgelocationR:tissueV = 0"
),
parameterNames = paste0("ridge", colnames(design))
)We can now falsify the null hypothesis of each contrast:
pe <- hypothesisTest(
object = pe, i = "proteins", contrast = L, overwrite = TRUE
)6.7.5 Evaluate results for contrast \(\log_2 FC_{V-A}^L\)
Let us retrieve the result table from the rowData. Note that the hypothesis testing results are stored in rowData columns named after the column names of the contrast matrix L. The first column contains the results for contrast \(\log_2 FC_{V-A}^L\).
inferenceLeft <- rowData(pe[["proteins"]])[[colnames(L)[1]]]
inferenceLeft$Protein <- rownames(inferenceLeft)
head(inferenceLeft) logFC se df t pval adjPval Protein
A0PJW6 0.00000000 5.509988e-10 14.003000 0.0000000 1.0000000 1 A0PJW6
A0PJZ3 NA NA NA NA NA NA A0PJZ3
A0PK00 NA NA 5.826529 NA NA NA A0PK00
A1A4S6 0.03452594 8.910408e-02 13.324734 0.3874788 0.7045204 1 A1A4S6
A1A5D9 NA NA NA NA NA NA A1A5D9
A1IGU5 -0.12078957 2.045995e-01 10.934858 -0.5903708 0.5669427 1 A1IGU5Notice that some rows contain missing values. This is because data modelling resulted in a fitError for some proteins, probably because not enough data was available for model fitting due to missing values in the quantitative data (see how to deal with fitErrors).
Volcano plot
Volcano plots are straightforward to generate from the inference table above. We also use ggrepel to annotate the 20 most significant proteins.
ggplot(inferenceLeft) +
aes(x = logFC, y = -log10(pval), color = adjPval < 0.05) +
geom_point() +
geom_text_repel(data = slice_min(inferenceLeft, adjPval, n = 20),
aes(label = Protein)) +
scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
ggtitle("log2 FC V-A left",
paste("Hypothesis test:", colnames(L)[1], "= 0"))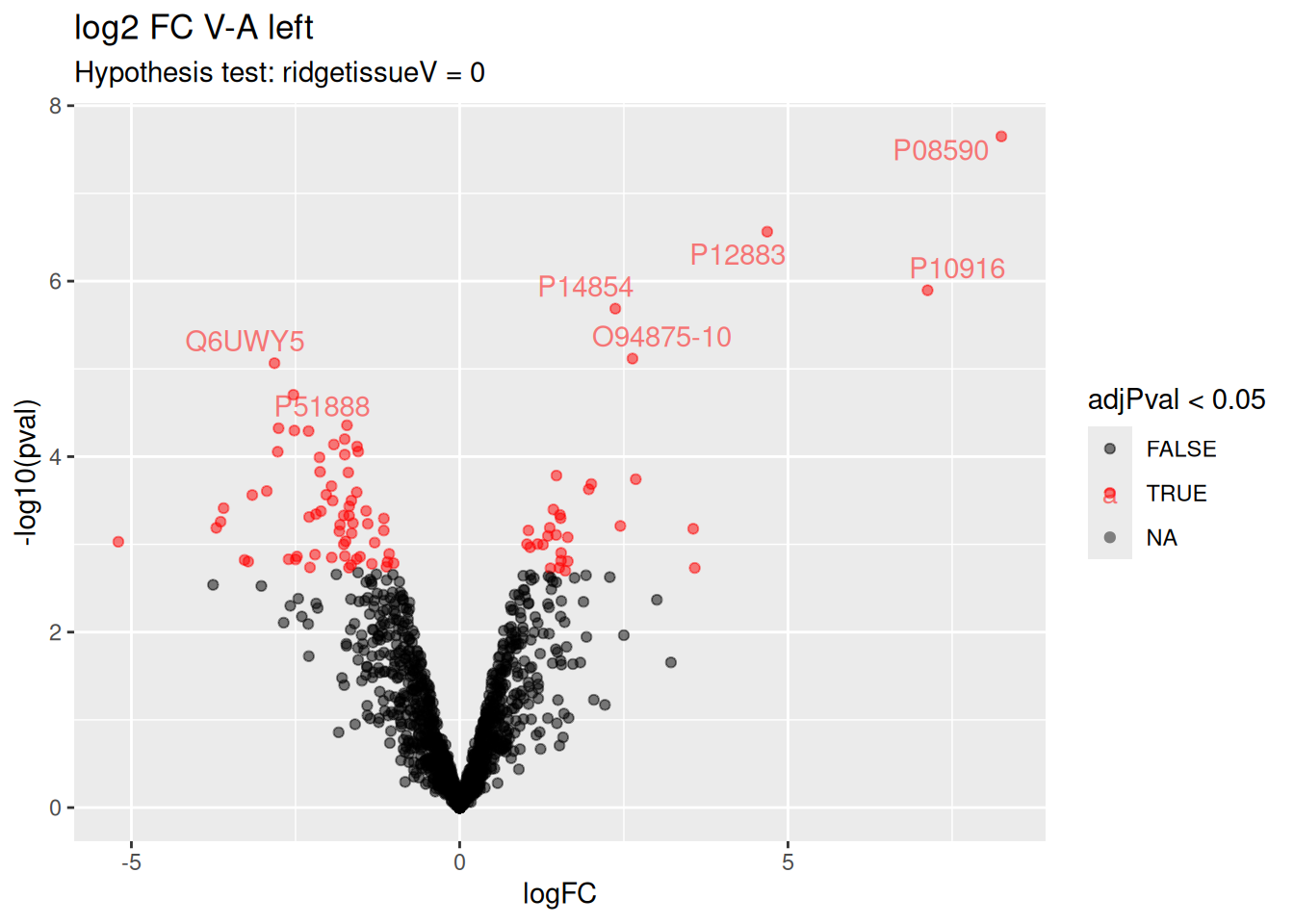
Heatmap
We can also build a heatmap for the significant proteins which are obtained by filtering the inference table. We first retrieve the data with proteins that are differentially abundant between the atrium and the ventriculum in the left heart.
sigNamesLeft <- inferenceLeft |>
filter(!is.na(adjPval), adjPval < 0.05) |>
pull()
se <- getWithColData(pe, "proteins")[sigNamesLeft, ]We then plot the protein-wise standardised data as an annotated heatmap.
quants <- t(scale(t(assay(se))))
library("ComplexHeatmap")
annotations <- columnAnnotation(
tissue = se$tissue,
location = se$location
)
set.seed(1234) ## annotation colours are randomly generated by default
Heatmap(
quants, name = "log2 intensity",
top_annotation = annotations
)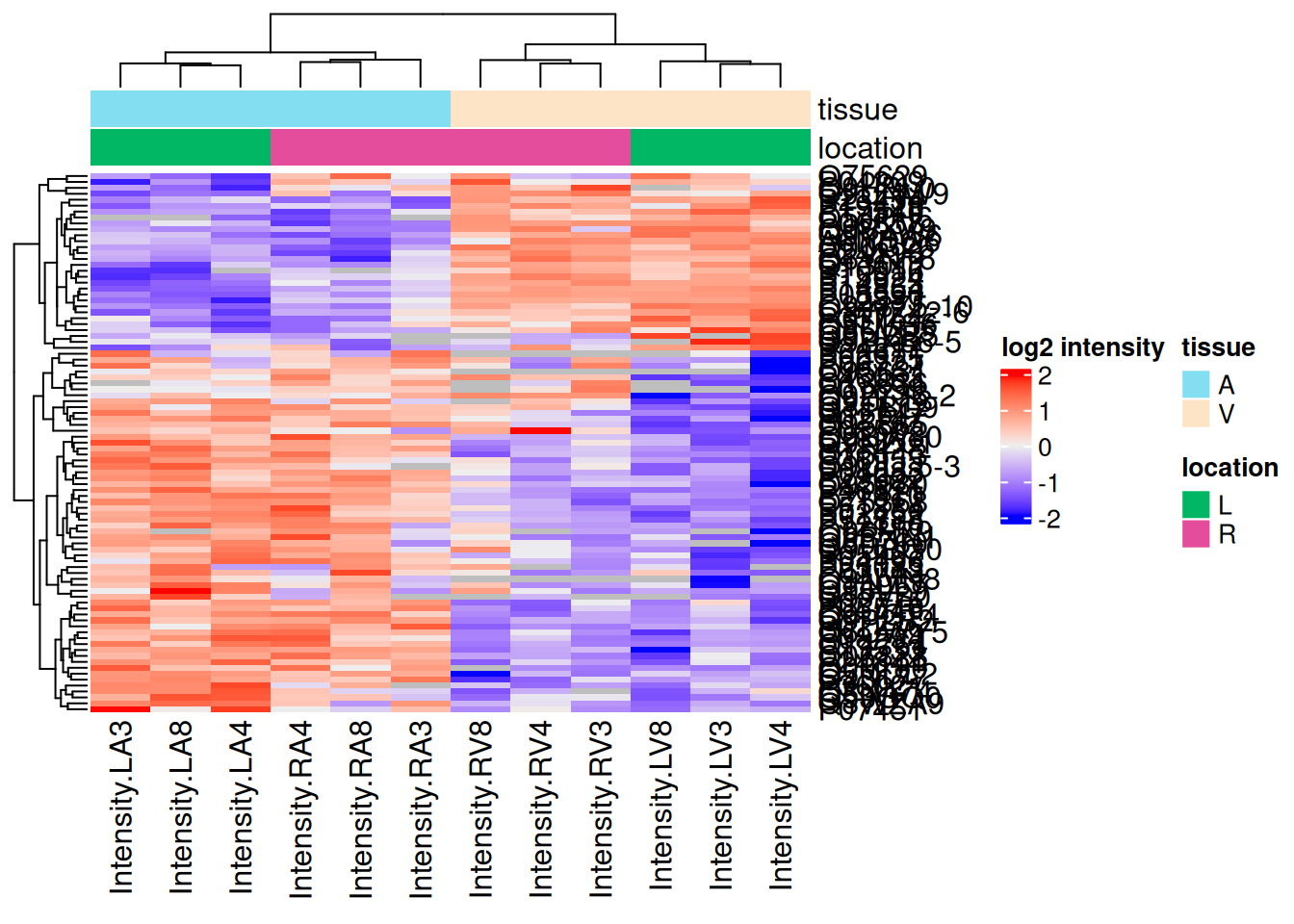
There are 91 proteins significantly differentially expressed at the 5% FDR level. Below you can find the list of significant proteins.
inferenceLeft |>
na.exclude() |>
filter(adjPval<0.05) |>
arrange(pval) |>
knitr::kable()| logFC | se | df | t | pval | adjPval | Protein | |
|---|---|---|---|---|---|---|---|
| P08590 | 8.250133 | 0.4618098 | 9.066700 | 17.864783 | 0.0000000 | 0.0000501 | P08590 |
| P12883 | 4.683827 | 0.3506520 | 9.108910 | 13.357477 | 0.0000003 | 0.0003054 | P12883 |
| P10916 | 7.126335 | 0.4767443 | 7.093703 | 14.947920 | 0.0000013 | 0.0009474 | P10916 |
| P14854 | 2.370452 | 0.2234186 | 9.066347 | 10.609916 | 0.0000021 | 0.0011498 | P14854 |
| O94875-10 | 2.631801 | 0.2944480 | 9.230071 | 8.938084 | 0.0000076 | 0.0032078 | O94875-10 |
| Q6UWY5 | -2.820577 | 0.3178826 | 9.147279 | -8.873014 | 0.0000086 | 0.0032078 | Q6UWY5 |
| P51888 | -2.532542 | 0.3183317 | 9.246559 | -7.955671 | 0.0000197 | 0.0063061 | P51888 |
| P46821 | -1.716407 | 0.2365827 | 9.150270 | -7.255001 | 0.0000439 | 0.0103944 | P46821 |
| Q8N474 | -2.758038 | 0.3551103 | 8.190289 | -7.766709 | 0.0000475 | 0.0103944 | Q8N474 |
| P21810 | -2.518077 | 0.3552103 | 9.230160 | -7.088977 | 0.0000504 | 0.0103944 | P21810 |
| P02747 | -2.301603 | 0.3282428 | 9.364965 | -7.011892 | 0.0000511 | 0.0103944 | P02747 |
| O75368 | -1.751397 | 0.2535261 | 9.191185 | -6.908151 | 0.0000632 | 0.0117700 | O75368 |
| O14967 | -1.916404 | 0.2835587 | 9.248331 | -6.758403 | 0.0000728 | 0.0122440 | O14967 |
| P05546 | -1.563360 | 0.2304074 | 9.089659 | -6.785196 | 0.0000767 | 0.0122440 | P05546 |
| P29622 | -1.544848 | 0.2320175 | 9.113749 | -6.658327 | 0.0000876 | 0.0122901 | P29622 |
| Q9ULL5-3 | -2.771336 | 0.3986314 | 8.505757 | -6.952128 | 0.0000879 | 0.0122901 | Q9ULL5-3 |
| P18428 | -1.750339 | 0.2688643 | 9.299328 | -6.510121 | 0.0000950 | 0.0124912 | P18428 |
| P08294 | -2.135352 | 0.3312298 | 9.307183 | -6.446739 | 0.0001021 | 0.0126793 | P08294 |
| Q8TBQ9 | -2.126623 | 0.3493479 | 9.446801 | -6.087408 | 0.0001491 | 0.0169428 | Q8TBQ9 |
| P00325 | -1.696574 | 0.2749298 | 9.177945 | -6.170934 | 0.0001515 | 0.0169428 | P00325 |
| P15924 | 1.473571 | 0.2403994 | 9.110066 | 6.129679 | 0.0001644 | 0.0175054 | P15924 |
| Q9UBB5 | 2.681925 | 0.3323530 | 6.082236 | 8.069506 | 0.0001809 | 0.0183864 | Q9UBB5 |
| P06858 | 2.005077 | 0.3377476 | 9.148010 | 5.936613 | 0.0002052 | 0.0199517 | P06858 |
| P24844 | -1.952282 | 0.3366253 | 9.433933 | -5.799568 | 0.0002167 | 0.0201925 | P24844 |
| P24311 | 1.966170 | 0.3414895 | 9.362276 | 5.757630 | 0.0002356 | 0.0210760 | P24311 |
| Q5JVS0 | -2.937575 | 0.3186422 | 5.020511 | -9.219040 | 0.0002467 | 0.0210902 | Q5JVS0 |
| O95865 | -1.567784 | 0.2751262 | 9.360986 | -5.698419 | 0.0002547 | 0.0210902 | O95865 |
| P02452 | -2.032726 | 0.3640935 | 9.585356 | -5.582980 | 0.0002720 | 0.0211347 | P02452 |
| P13533 | -3.159311 | 0.5620164 | 9.431456 | -5.621385 | 0.0002741 | 0.0211347 | P13533 |
| Q9P2B2 | -1.649939 | 0.2981357 | 9.357789 | -5.534187 | 0.0003166 | 0.0229231 | Q9P2B2 |
| Q15113 | -1.934718 | 0.3529607 | 9.536113 | -5.481398 | 0.0003178 | 0.0229231 | Q15113 |
| P02743 | -1.682963 | 0.3088914 | 9.259904 | -5.448396 | 0.0003682 | 0.0257297 | P02743 |
| P23083 | -3.595505 | 0.5864530 | 7.380951 | -6.130935 | 0.0003865 | 0.0259912 | P23083 |
| P23434 | 1.426496 | 0.2644910 | 9.231040 | 5.393363 | 0.0004005 | 0.0259912 | P23434 |
| P04196 | -1.424906 | 0.2661117 | 9.273169 | -5.354540 | 0.0004154 | 0.0259912 | P04196 |
| Q9BW30 | -2.113450 | 0.4001977 | 9.534123 | -5.281013 | 0.0004185 | 0.0259912 | Q9BW30 |
| O43677 | -2.187788 | 0.4161198 | 9.401692 | -5.257592 | 0.0004526 | 0.0262839 | O43677 |
| Q9UKS6 | 1.527078 | 0.2923847 | 9.488160 | 5.222840 | 0.0004608 | 0.0262839 | Q9UKS6 |
| Q53GQ0 | -1.766962 | 0.3426900 | 9.718619 | -5.156155 | 0.0004684 | 0.0262839 | Q53GQ0 |
| P36955 | -1.684290 | 0.3276053 | 9.772134 | -5.141217 | 0.0004702 | 0.0262839 | P36955 |
| P05997 | -2.292742 | 0.4438855 | 9.559204 | -5.165165 | 0.0004876 | 0.0263397 | P05997 |
| P04209 | 1.537844 | 0.2981332 | 9.495921 | 5.158245 | 0.0005029 | 0.0263397 | P04209 |
| Q14764 | -1.154973 | 0.2205762 | 9.165409 | -5.236163 | 0.0005065 | 0.0263397 | Q14764 |
| O95631 | -3.641005 | 0.4782087 | 5.133102 | -7.613842 | 0.0005523 | 0.0280667 | O95631 |
| P51884 | -1.625915 | 0.3221562 | 9.576049 | -5.046979 | 0.0005730 | 0.0283194 | P51884 |
| P08582 | -1.400068 | 0.2752535 | 9.355058 | -5.086468 | 0.0005826 | 0.0283194 | P08582 |
| Q16647 | -1.821645 | 0.3658315 | 9.742336 | -4.979465 | 0.0005991 | 0.0285012 | Q16647 |
| P19429 | 2.446925 | 0.4900303 | 9.586884 | 4.993416 | 0.0006163 | 0.0287104 | P19429 |
| Q6YN16 | 1.372126 | 0.2728193 | 9.276732 | 5.029431 | 0.0006473 | 0.0289927 | Q6YN16 |
| P01699 | -3.706945 | 0.5955534 | 6.325570 | -6.224371 | 0.0006483 | 0.0289927 | P01699 |
| Q9UNW9 | 3.556427 | 0.7181405 | 9.536696 | 4.952272 | 0.0006641 | 0.0291146 | Q9UNW9 |
| P14923 | 1.046597 | 0.2091414 | 9.171357 | 5.004255 | 0.0006940 | 0.0293444 | P14923 |
| P04083 | -1.155807 | 0.2326322 | 9.318065 | -4.968389 | 0.0006956 | 0.0293444 | P04083 |
| Q96LL9 | -1.832427 | 0.3733546 | 9.526194 | -4.908006 | 0.0007099 | 0.0293942 | Q96LL9 |
| O95980 | -1.644847 | 0.3372152 | 9.498408 | -4.877737 | 0.0007478 | 0.0304004 | O95980 |
| Q00G26 | 1.468999 | 0.2999726 | 9.271814 | 4.897112 | 0.0007803 | 0.0311574 | Q00G26 |
| Q13011 | 1.343312 | 0.2779008 | 9.478440 | 4.833782 | 0.0008015 | 0.0314398 | Q13011 |
| Q9BX66-5 | 1.645228 | 0.3003872 | 7.236228 | 5.477024 | 0.0008305 | 0.0320157 | Q9BX66-5 |
| Q9UBG0 | -1.737280 | 0.3711535 | 9.768266 | -4.680758 | 0.0009230 | 0.0346124 | Q9UBG0 |
| Q9NVN8 | -5.198643 | 0.7881637 | 5.337400 | -6.595893 | 0.0009338 | 0.0346124 | Q9NVN8 |
| P12110 | -1.294302 | 0.2752573 | 9.536991 | -4.702153 | 0.0009541 | 0.0346124 | P12110 |
| P17540 | 1.186827 | 0.2524879 | 9.408560 | 4.700530 | 0.0009922 | 0.0346124 | P17540 |
| Q8WZ42-6 | 1.025527 | 0.2181058 | 9.391830 | 4.701968 | 0.0009949 | 0.0346124 | Q8WZ42-6 |
| Q9UL18 | -1.765694 | 0.3684251 | 8.951891 | -4.792544 | 0.0009988 | 0.0346124 | Q9UL18 |
| A6NDG6 | 1.268609 | 0.2689144 | 9.276465 | 4.717521 | 0.0010062 | 0.0346124 | A6NDG6 |
| Q9Y4W6 | 1.073065 | 0.2294084 | 9.235088 | 4.677530 | 0.0010787 | 0.0365449 | Q9Y4W6 |
| P24298 | 1.544611 | 0.3397789 | 9.384519 | 4.545929 | 0.0012525 | 0.0418012 | P24298 |
| P46063 | -1.073446 | 0.2365976 | 9.340311 | -4.537009 | 0.0012845 | 0.0422366 | P46063 |
| P36021 | -2.202548 | 0.4760910 | 8.828176 | -4.626317 | 0.0013081 | 0.0423886 | P36021 |
| Q5NDL2 | -1.747813 | 0.3912896 | 9.517072 | -4.466802 | 0.0013600 | 0.0429751 | Q5NDL2 |
| Q13636 | -2.478227 | 0.4646276 | 6.499442 | -5.333792 | 0.0013751 | 0.0429751 | Q13636 |
| P02775 | -1.516837 | 0.3394756 | 9.442684 | -4.468178 | 0.0013838 | 0.0429751 | P02775 |
| Q9BXN1 | -1.948674 | 0.4430265 | 9.779246 | -4.398551 | 0.0014117 | 0.0432408 | Q9BXN1 |
| Q9NZ01 | -1.568868 | 0.3603847 | 9.896186 | -4.353317 | 0.0014718 | 0.0436957 | Q9NZ01 |
| Q92736-2 | -2.605932 | 0.5910197 | 9.526607 | -4.409213 | 0.0014794 | 0.0436957 | Q92736-2 |
| O60760 | -2.498746 | 0.5569448 | 9.077881 | -4.486523 | 0.0014858 | 0.0436957 | O60760 |
| Q06828 | -3.276730 | 0.7507098 | 9.730028 | -4.364843 | 0.0015047 | 0.0436957 | Q06828 |
| O75629 | 1.543697 | 0.3542839 | 9.693237 | 4.357233 | 0.0015361 | 0.0437116 | O75629 |
| Q9HBL0 | 1.646254 | 0.3543908 | 8.180895 | 4.645306 | 0.0015594 | 0.0437116 | Q9HBL0 |
| O00180 | -3.220740 | 0.7131678 | 8.732659 | -4.516103 | 0.0015702 | 0.0437116 | O00180 |
| P06727 | -1.098656 | 0.2488030 | 9.225409 | -4.415767 | 0.0015835 | 0.0437116 | P06727 |
| Q8WZA9 | -1.005633 | 0.2319000 | 9.553531 | -4.336494 | 0.0016406 | 0.0447356 | Q8WZA9 |
| P02776 | -1.337487 | 0.3054296 | 9.240633 | -4.379034 | 0.0016652 | 0.0448599 | P02776 |
| Q9UGT4 | -1.651943 | 0.3842304 | 9.601092 | -4.299354 | 0.0017164 | 0.0456878 | Q9UGT4 |
| P07451 | -1.114780 | 0.2610269 | 9.585814 | -4.270745 | 0.0017998 | 0.0465444 | P07451 |
| Q96H79 | -2.280431 | 0.4560710 | 6.634593 | -5.000166 | 0.0018317 | 0.0465444 | Q96H79 |
| P02671 | -1.686681 | 0.3221285 | 6.105609 | -5.236051 | 0.0018443 | 0.0465444 | P02671 |
| Q86VU5 | 1.516645 | 0.3572766 | 9.638787 | 4.245018 | 0.0018493 | 0.0465444 | Q86VU5 |
| Q5JPH6 | 3.579987 | 0.7035217 | 6.397711 | 5.088666 | 0.0018571 | 0.0465444 | Q5JPH6 |
| P35754 | 1.382605 | 0.3285348 | 9.831307 | 4.208396 | 0.0018734 | 0.0465444 | P35754 |
| Q9BXV9 | 1.608759 | 0.3856887 | 9.805041 | 4.171135 | 0.0019979 | 0.0490914 | Q9BXV9 |
6.7.6 Evaluate results for contrast \(\log_2 FC_{V-A}^R\)
Let us retrieve the result table from the rowData. The second column contains the results for contrast \(\log_2 FC_{V-A}^R\).
inferenceRight <- rowData(pe[["proteins"]])[[colnames(L)[2]]]
inferenceRight$Protein <- rownames(inferenceRight)
head(inferenceRight) logFC se df t pval adjPval
A0PJW6 0.00000000 5.509988e-10 14.003000 0.0000000 1.00000000 1.0000000
A0PJZ3 NA NA NA NA NA NA
A0PK00 NA NA 5.826529 NA NA NA
A1A4S6 0.04979859 8.881359e-02 13.324734 0.5607091 0.58430170 1.0000000
A1A5D9 NA NA NA NA NA NA
A1IGU5 -0.40996946 2.015378e-01 10.934858 -2.0342065 0.06691788 0.3697382
Protein
A0PJW6 A0PJW6
A0PJZ3 A0PJZ3
A0PK00 A0PK00
A1A4S6 A1A4S6
A1A5D9 A1A5D9
A1IGU5 A1IGU5Volcano plot
Volcano plots are straightforward to generate from the inference table above. We also use ggrepel to annotate the 20 most significant proteins.
ggplot(inferenceRight) +
aes(x = logFC, y = -log10(pval), color = adjPval < 0.05) +
geom_point() +
geom_text_repel(data = slice_min(inferenceRight, adjPval, n = 20),
aes(label = Protein)) +
scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
ggtitle("log2 FC V-A Right",
paste("Hypothesis test:", colnames(L)[2], "= 0"))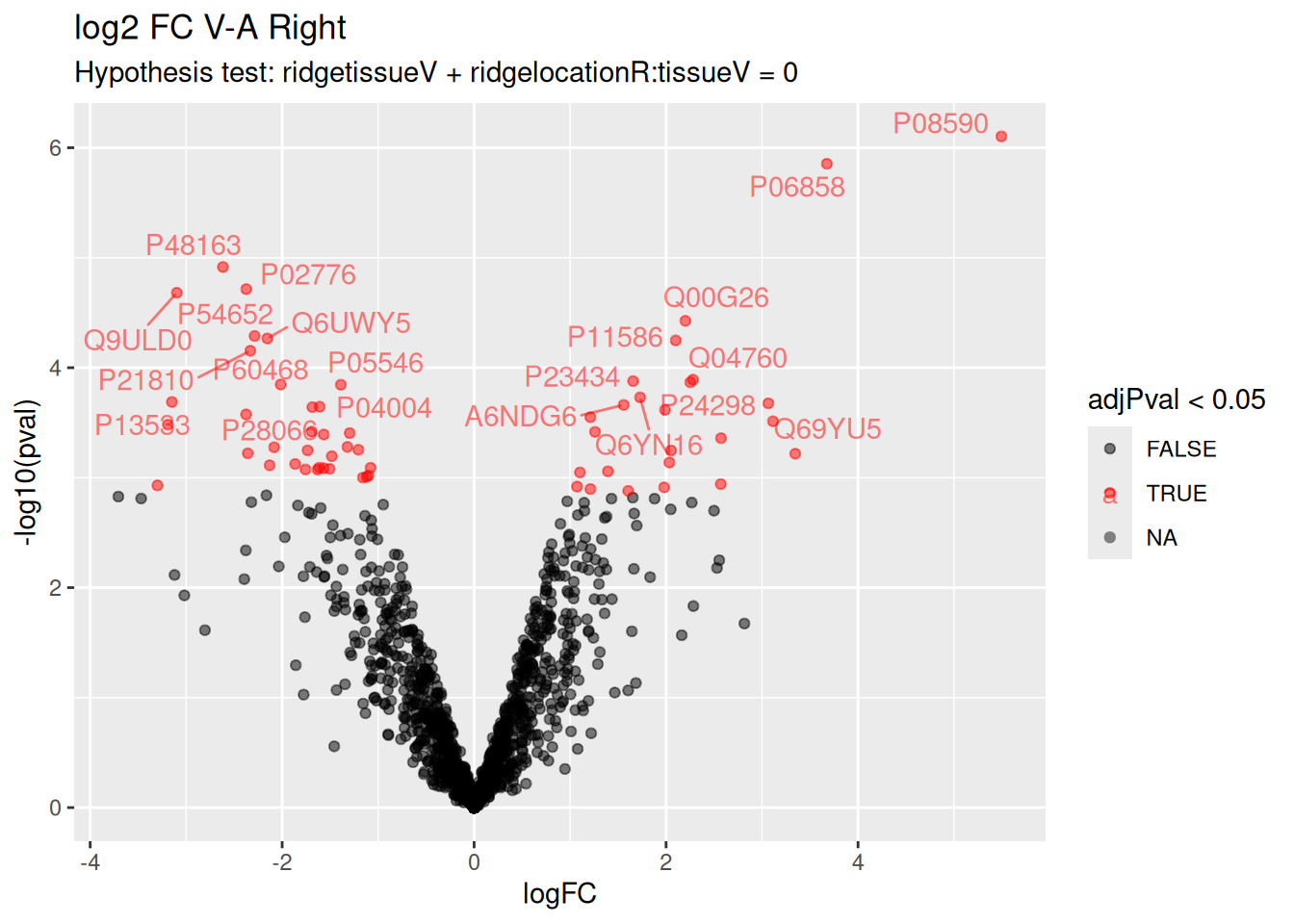
Heatmap
We can also build a heatmap for the significant proteins which are obtained by filtering the inference table1.
sigNamesRight <- inferenceRight |>
filter(!is.na(adjPval), adjPval < 0.05) |>
pull()
se <- getWithColData(pe, "proteins")[sigNamesRight, ]
quants <- t(scale(t(assay(se))))
set.seed(1234) ## annotation colours are randomly generated by default
Heatmap(
quants, name = "log2 intensity",
top_annotation = annotations
)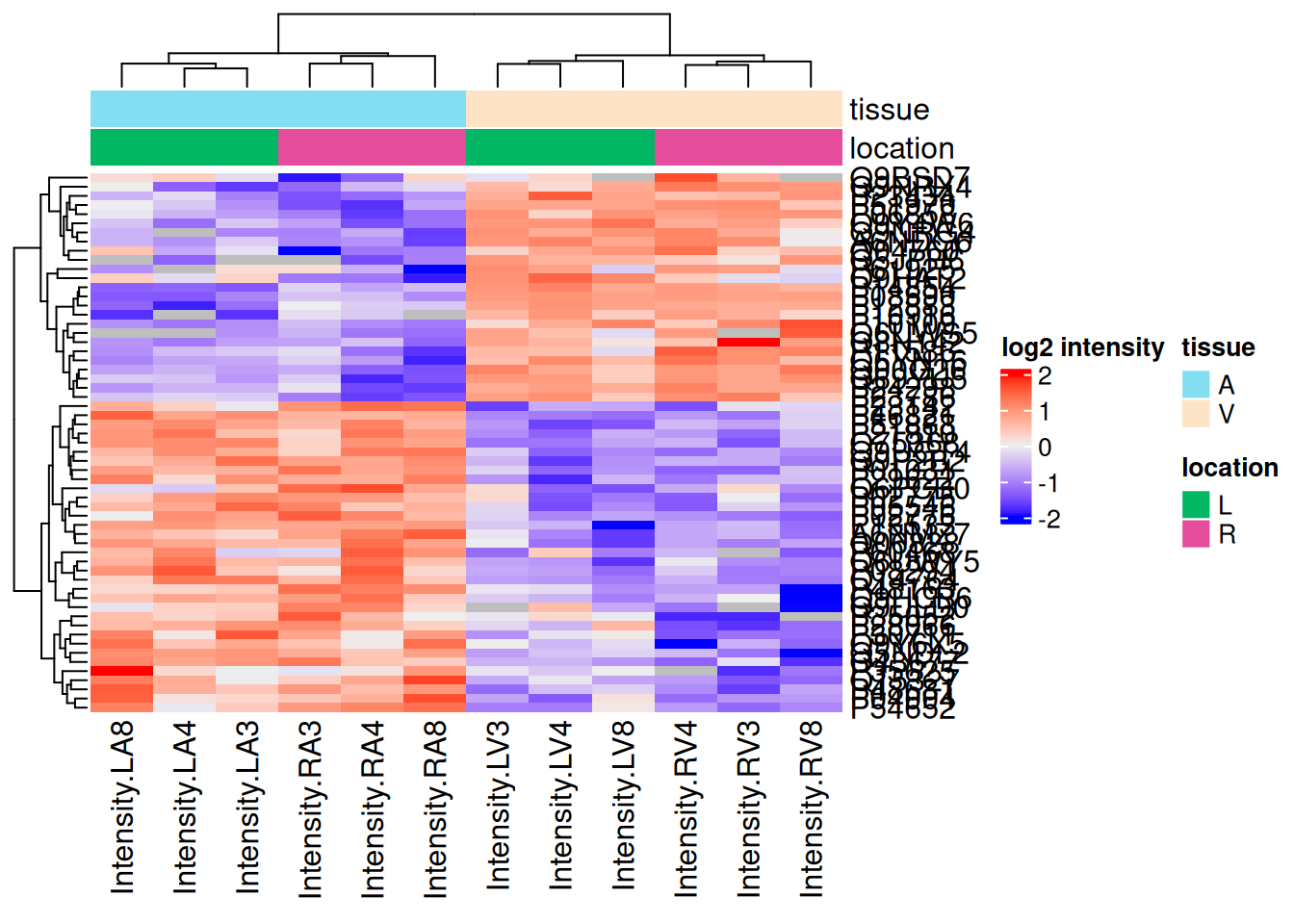
There are 59 proteins significantly differentially expressed at the 5% FDR level.
Below you can find the list of significant proteins.
inferenceRight |>
na.exclude() |>
filter(adjPval<0.05) |>
arrange(pval) |>
knitr::kable()| logFC | se | df | t | pval | adjPval | Protein | |
|---|---|---|---|---|---|---|---|
| P08590 | 5.493574 | 0.4626211 | 9.066700 | 11.874888 | 0.0000008 | 0.0015317 | P08590 |
| P06858 | 3.674709 | 0.3338983 | 9.148010 | 11.005474 | 0.0000014 | 0.0015317 | P06858 |
| P48163 | -2.616881 | 0.3097355 | 9.233764 | -8.448762 | 0.0000121 | 0.0088573 | P48163 |
| P02776 | -2.374280 | 0.2974779 | 9.240633 | -7.981367 | 0.0000193 | 0.0091147 | P02776 |
| Q9ULD0 | -3.097487 | 0.3131518 | 7.104538 | -9.891328 | 0.0000208 | 0.0091147 | Q9ULD0 |
| Q00G26 | 2.200504 | 0.2999726 | 9.271814 | 7.335685 | 0.0000375 | 0.0136795 | Q00G26 |
| P54652 | -2.287138 | 0.3255640 | 9.325197 | -7.025158 | 0.0000515 | 0.0137287 | P54652 |
| Q6UWY5 | -2.154394 | 0.3049324 | 9.147279 | -7.065153 | 0.0000542 | 0.0137287 | Q6UWY5 |
| P11586 | 2.100538 | 0.3026749 | 9.333226 | 6.939915 | 0.0000565 | 0.0137287 | P11586 |
| P21810 | -2.331556 | 0.3429892 | 9.230160 | -6.797753 | 0.0000702 | 0.0153595 | P21810 |
| Q04760 | 2.281002 | 0.3674889 | 9.441126 | 6.206996 | 0.0001286 | 0.0208338 | Q04760 |
| P23434 | 1.656292 | 0.2644910 | 9.231040 | 6.262189 | 0.0001323 | 0.0208338 | P23434 |
| P24298 | 2.252174 | 0.3642189 | 9.384519 | 6.183572 | 0.0001358 | 0.0208338 | P24298 |
| P60468 | -2.014787 | 0.3022799 | 8.191586 | -6.665302 | 0.0001422 | 0.0208338 | P60468 |
| P05546 | -1.388646 | 0.2220578 | 9.089659 | -6.253532 | 0.0001428 | 0.0208338 | P05546 |
| Q6YN16 | 1.728901 | 0.2895814 | 9.276732 | 5.970346 | 0.0001861 | 0.0237989 | Q6YN16 |
| P13533 | -3.148481 | 0.5388200 | 9.431456 | -5.843288 | 0.0002050 | 0.0237989 | P13533 |
| Q69YU5 | 3.065356 | 0.5307692 | 9.579396 | 5.775308 | 0.0002110 | 0.0237989 | Q69YU5 |
| A6NDG6 | 1.557838 | 0.2665039 | 9.276465 | 5.845460 | 0.0002180 | 0.0237989 | A6NDG6 |
| P04004 | -1.609110 | 0.2765621 | 9.270800 | -5.818258 | 0.0002263 | 0.0237989 | P04004 |
| P28066 | -1.685066 | 0.2929535 | 9.457629 | -5.751991 | 0.0002284 | 0.0237989 | P28066 |
| P12883 | 1.989033 | 0.3417758 | 9.108910 | 5.819703 | 0.0002417 | 0.0240397 | P12883 |
| O43677 | -2.375819 | 0.4202739 | 9.401692 | -5.653026 | 0.0002660 | 0.0253014 | O43677 |
| P23786 | 1.210900 | 0.2128018 | 9.134748 | 5.690270 | 0.0002820 | 0.0257048 | P23786 |
| P10916 | 3.113228 | 0.4767443 | 7.093703 | 6.530185 | 0.0003069 | 0.0268623 | P10916 |
| P35625 | -3.190450 | 0.5540567 | 8.562007 | -5.758346 | 0.0003299 | 0.0277622 | P35625 |
| P30711 | -1.692001 | 0.3157636 | 9.492387 | -5.358443 | 0.0003818 | 0.0295584 | P30711 |
| P14854 | 1.259547 | 0.2300868 | 9.066347 | 5.474224 | 0.0003831 | 0.0295584 | P14854 |
| P29622 | -1.296379 | 0.2383018 | 9.113749 | -5.440070 | 0.0003935 | 0.0295584 | P29622 |
| Q15327 | -1.566469 | 0.2941564 | 9.451901 | -5.325292 | 0.0004053 | 0.0295584 | Q15327 |
| Q9NRG4 | 2.572149 | 0.4631363 | 8.484155 | 5.553763 | 0.0004377 | 0.0308916 | Q9NRG4 |
| O75368 | -1.320075 | 0.2537600 | 9.191185 | -5.202062 | 0.0005256 | 0.0344087 | O75368 |
| Q5NDL2 | -2.083671 | 0.4071966 | 9.517072 | -5.117114 | 0.0005290 | 0.0344087 | Q5NDL2 |
| P01031 | -1.205507 | 0.2348255 | 9.289894 | -5.133627 | 0.0005579 | 0.0344087 | P01031 |
| Q6PCB0 | -1.734824 | 0.3399387 | 9.378729 | -5.103342 | 0.0005646 | 0.0344087 | Q6PCB0 |
| P61925 | 2.051193 | 0.3786314 | 8.266540 | 5.417388 | 0.0005661 | 0.0344087 | P61925 |
| A6NMZ7 | -2.357794 | 0.4729659 | 9.707078 | -4.985124 | 0.0006007 | 0.0348990 | A6NMZ7 |
| Q5JPH6 | 3.345723 | 0.5352998 | 6.397711 | 6.250186 | 0.0006061 | 0.0348990 | Q5JPH6 |
| Q9P2B2 | -1.483082 | 0.2953969 | 9.357789 | -5.020641 | 0.0006381 | 0.0358009 | Q9P2B2 |
| Q9HAT2 | 2.033947 | 0.4116210 | 9.296680 | 4.941310 | 0.0007275 | 0.0385182 | Q9HAT2 |
| Q9UGT4 | -1.864637 | 0.3842304 | 9.601092 | -4.852913 | 0.0007514 | 0.0385182 | Q9UGT4 |
| P23142 | -2.130549 | 0.4396656 | 9.545973 | -4.845840 | 0.0007718 | 0.0385182 | P23142 |
| P08294 | -1.614308 | 0.3320461 | 9.307183 | -4.861700 | 0.0008114 | 0.0385182 | P08294 |
| Q14764 | -1.079085 | 0.2205762 | 9.165409 | -4.892120 | 0.0008127 | 0.0385182 | Q14764 |
| P35052 | -1.566974 | 0.3100259 | 8.489597 | -5.054332 | 0.0008208 | 0.0385182 | P35052 |
| P51888 | -1.505290 | 0.3098730 | 9.246559 | -4.857764 | 0.0008314 | 0.0385182 | P51888 |
| Q9HCB6 | -1.756881 | 0.3660009 | 9.478445 | -4.800210 | 0.0008413 | 0.0385182 | Q9HCB6 |
| P02775 | -1.630806 | 0.3394307 | 9.442684 | -4.804531 | 0.0008450 | 0.0385182 | P02775 |
| Q8N142 | 1.394024 | 0.2921992 | 9.488674 | 4.770801 | 0.0008753 | 0.0390833 | Q8N142 |
| Q9Y4W6 | 1.102812 | 0.2294084 | 9.235088 | 4.807199 | 0.0008963 | 0.0392226 | Q9Y4W6 |
| P48681 | -1.101098 | 0.2312917 | 9.238145 | -4.760646 | 0.0009568 | 0.0410483 | P48681 |
| P46821 | -1.120872 | 0.2355359 | 9.150270 | -4.758817 | 0.0009851 | 0.0412685 | P46821 |
| Q9Y6X5 | -1.159408 | 0.2466137 | 9.378833 | -4.701313 | 0.0009996 | 0.0412685 | Q9Y6X5 |
| Q9BSD7 | 2.569845 | 0.5189540 | 7.936523 | 4.951970 | 0.0011446 | 0.0463795 | Q9BSD7 |
| Q06828 | -3.298913 | 0.7287820 | 9.730028 | -4.526612 | 0.0011758 | 0.0467768 | Q06828 |
| P51970 | 1.071905 | 0.2350925 | 9.453305 | 4.559505 | 0.0012049 | 0.0470148 | P51970 |
| Q6UWS5 | 1.979951 | 0.3609481 | 6.427167 | 5.485418 | 0.0012248 | 0.0470148 | Q6UWS5 |
| P10109 | 1.211344 | 0.2678468 | 9.462988 | 4.522524 | 0.0012695 | 0.0478898 | P10109 |
| Q9NRX4 | 1.605283 | 0.3585462 | 9.576287 | 4.477201 | 0.0013185 | 0.0488954 | Q9NRX4 |
6.7.7 Evaluate results average contrast \(\log_2 FC_{V-A}\)
Let us retrieve the result table from the rowData. The second column contains the results for contrast \(\log_2 FC_{V-A}\).
inferenceAvg <- rowData(pe[["proteins"]])[[colnames(L)[3]]]
inferenceAvg$Protein <- rownames(inferenceAvg)
head(inferenceAvg) logFC se df t pval adjPval
A0PJW6 0.00000000 3.896150e-10 14.003000 0.0000000 1.00000000 1.0000000
A0PJZ3 NA NA NA NA NA NA
A0PK00 NA NA 5.826529 NA NA NA
A1A4S6 0.04216227 6.290247e-02 13.324734 0.6702799 0.51412912 1.0000000
A1A5D9 NA NA NA NA NA NA
A1IGU5 -0.26537952 1.435953e-01 10.934858 -1.8481073 0.09179013 0.3358475
Protein
A0PJW6 A0PJW6
A0PJZ3 A0PJZ3
A0PK00 A0PK00
A1A4S6 A1A4S6
A1A5D9 A1A5D9
A1IGU5 A1IGU5Volcano plot
Volcano plots are straightforward to generate from the inference table above. We also use ggrepel to annotate the 20 most significant proteins.
ggplot(inferenceAvg) +
aes(x = logFC, y = -log10(pval), color = adjPval < 0.05) +
geom_point() +
geom_text_repel(data = slice_min(inferenceAvg, adjPval, n = 20),
aes(label = Protein)) +
scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
ggtitle("log2 FC V-A Right",
paste("Hypothesis test:", colnames(L)[2], "= 0"))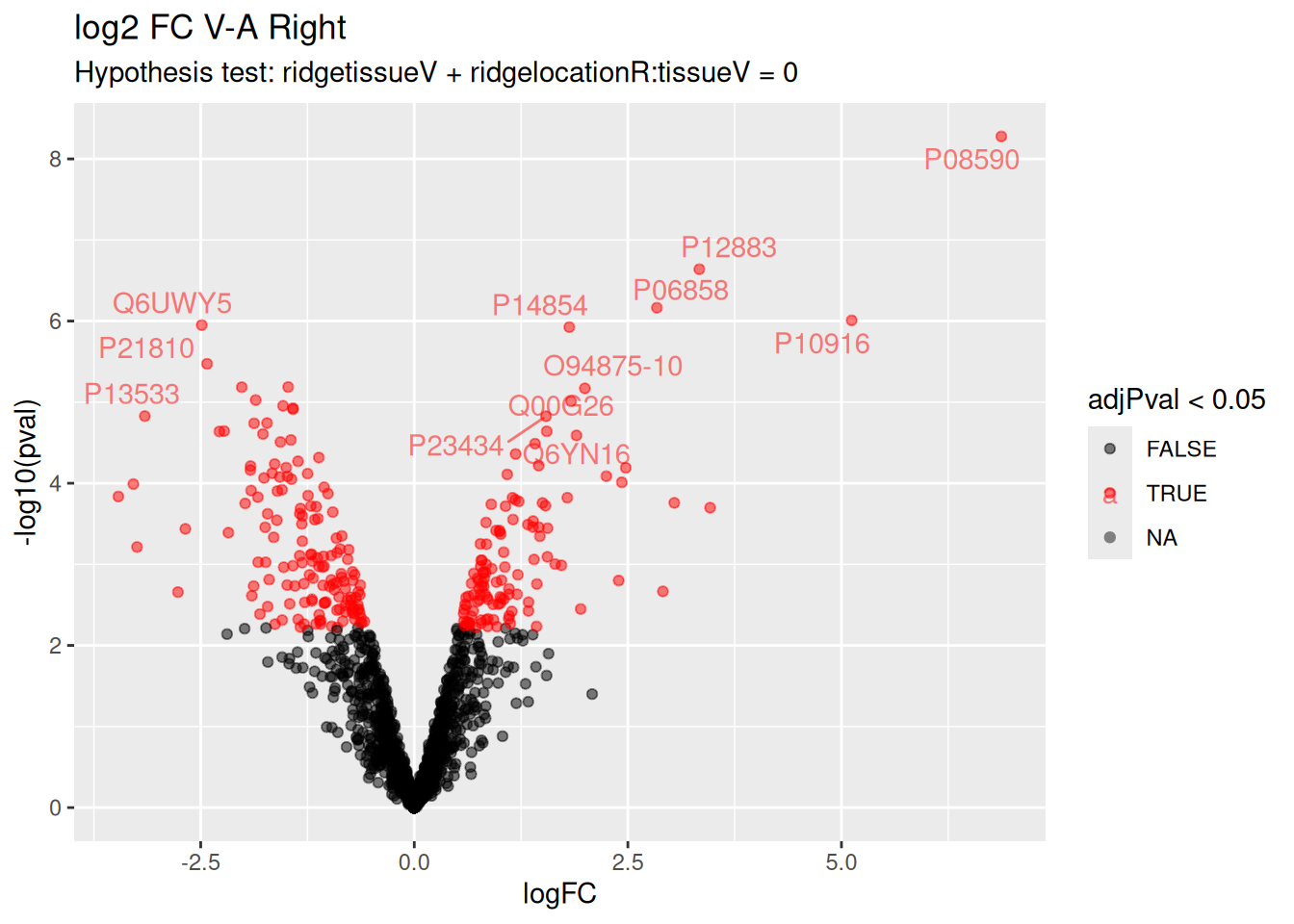
Heatmap
We can also build a heatmap for the significant proteins which are obtained by filtering the inference table.
sigNamesAvg <- inferenceAvg |>
filter(!is.na(adjPval), adjPval < 0.05) |>
pull()
se <- getWithColData(pe, "proteins")[sigNamesAvg, ]
quants <- t(scale(t(assay(se))))
set.seed(1234) ## annotation colours are randomly generated by default
Heatmap(
quants, name = "log2 intensity",
top_annotation = annotations
)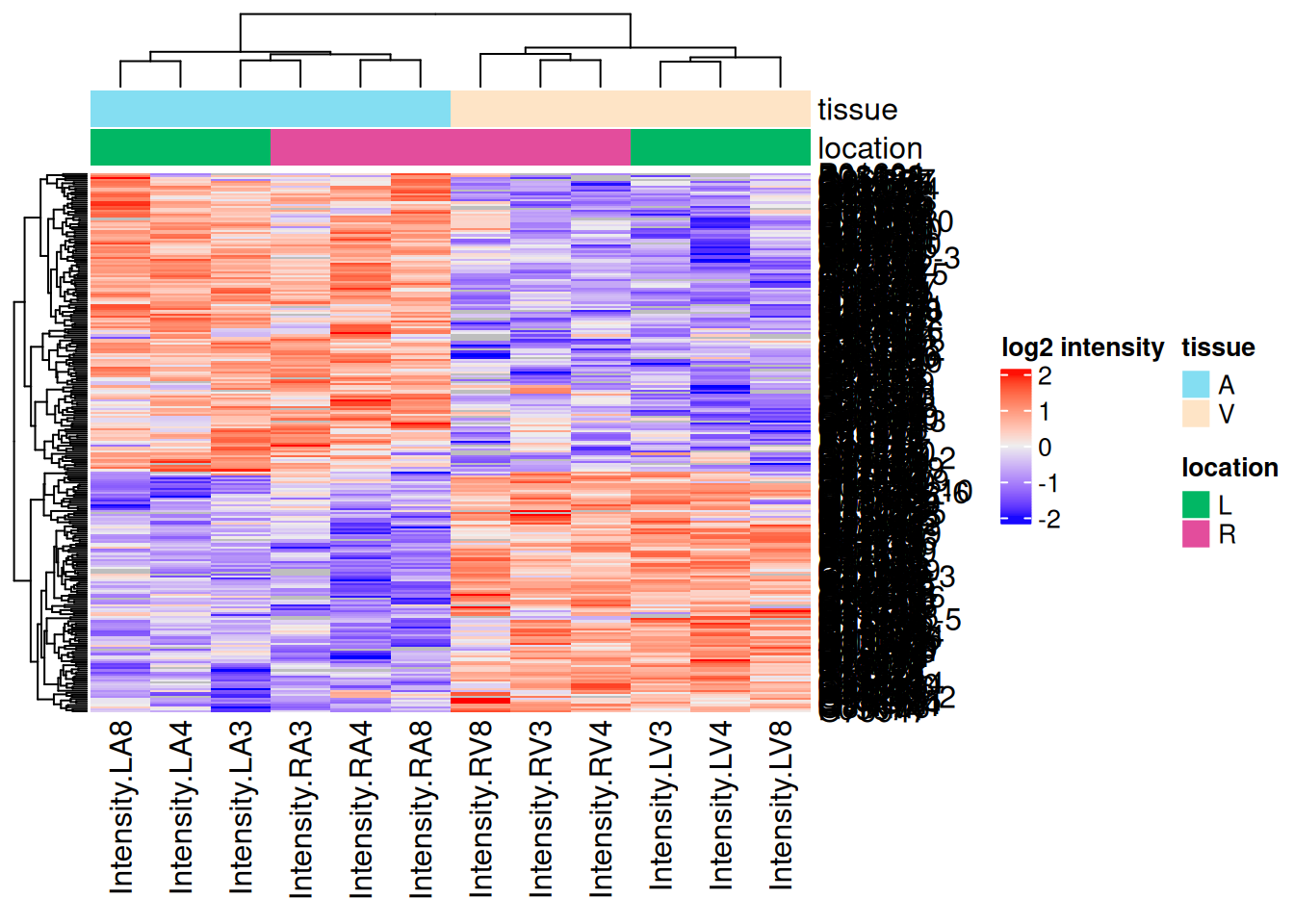
There are 264 proteins significantly differentially expressed at the 5% FDR level.
Below you can find the list of significant proteins.
inferenceAvg |>
na.exclude() |>
filter(adjPval<0.05) |>
arrange(pval) |>
knitr::kable()| logFC | se | df | t | pval | adjPval | Protein | |
|---|---|---|---|---|---|---|---|
| P08590 | 6.8718531 | 0.3268358 | 9.066700 | 21.025398 | 0.0000000 | 0.0000115 | P08590 |
| P12883 | 3.3364301 | 0.2448303 | 9.108910 | 13.627520 | 0.0000002 | 0.0002510 | P12883 |
| P06858 | 2.8398932 | 0.2374666 | 9.148010 | 11.959126 | 0.0000007 | 0.0004333 | P06858 |
| P10916 | 5.1197819 | 0.3298586 | 7.093703 | 15.521141 | 0.0000010 | 0.0004333 | P10916 |
| Q6UWY5 | -2.4874855 | 0.2202460 | 9.147279 | -11.294126 | 0.0000011 | 0.0004333 | Q6UWY5 |
| P14854 | 1.8149997 | 0.1603557 | 9.066347 | 11.318585 | 0.0000012 | 0.0004333 | P14854 |
| P21810 | -2.4248168 | 0.2462386 | 9.230160 | -9.847427 | 0.0000034 | 0.0010530 | P21810 |
| P05546 | -1.4760026 | 0.1599979 | 9.089659 | -9.225140 | 0.0000065 | 0.0014784 | P05546 |
| P51888 | -2.0189161 | 0.2221104 | 9.246559 | -9.089697 | 0.0000065 | 0.0014784 | P51888 |
| O94875-10 | 1.9967297 | 0.2201929 | 9.230071 | 9.068093 | 0.0000068 | 0.0014784 | O94875-10 |
| P02776 | -1.8558833 | 0.2131785 | 9.240633 | -8.705771 | 0.0000094 | 0.0017739 | P02776 |
| Q00G26 | 1.8347517 | 0.2121126 | 9.271814 | 8.649893 | 0.0000097 | 0.0017739 | Q00G26 |
| O75368 | -1.5357360 | 0.1791590 | 9.191185 | -8.571914 | 0.0000111 | 0.0017804 | O75368 |
| P29622 | -1.4206134 | 0.1659883 | 9.113749 | -8.558513 | 0.0000119 | 0.0017804 | P29622 |
| P46821 | -1.4186399 | 0.1668418 | 9.150270 | -8.502903 | 0.0000122 | 0.0017804 | P46821 |
| P13533 | -3.1538958 | 0.3885644 | 9.431456 | -8.116790 | 0.0000149 | 0.0019214 | P13533 |
| P23434 | 1.5413943 | 0.1870234 | 9.231040 | 8.241720 | 0.0000149 | 0.0019214 | P23434 |
| P48163 | -1.7231690 | 0.2140965 | 9.233764 | -8.048562 | 0.0000181 | 0.0021010 | P48163 |
| P08294 | -1.8748304 | 0.2345078 | 9.307183 | -7.994747 | 0.0000182 | 0.0021010 | P08294 |
| Q8N474 | -2.2252733 | 0.2593043 | 8.190289 | -8.581705 | 0.0000227 | 0.0022887 | Q8N474 |
| Q6YN16 | 1.5505133 | 0.1989270 | 9.276732 | 7.794385 | 0.0000229 | 0.0022887 | Q6YN16 |
| O43677 | -2.2818039 | 0.2956909 | 9.401692 | -7.716855 | 0.0000230 | 0.0022887 | O43677 |
| P54652 | -1.7712555 | 0.2302085 | 9.325197 | -7.694137 | 0.0000247 | 0.0023452 | P54652 |
| P24298 | 1.8983921 | 0.2490507 | 9.384519 | 7.622512 | 0.0000257 | 0.0023452 | P24298 |
| P18428 | -1.4437423 | 0.1912298 | 9.299328 | -7.549776 | 0.0000293 | 0.0025615 | P18428 |
| Q9P2B2 | -1.5665103 | 0.2098477 | 9.357789 | -7.464987 | 0.0000310 | 0.0026079 | Q9P2B2 |
| A6NDG6 | 1.4132236 | 0.1893082 | 9.276465 | 7.465199 | 0.0000325 | 0.0026334 | A6NDG6 |
| P15924 | 1.1865540 | 0.1629059 | 9.110066 | 7.283678 | 0.0000436 | 0.0034053 | P15924 |
| Q14764 | -1.1170292 | 0.1559709 | 9.165409 | -7.161778 | 0.0000482 | 0.0036399 | Q14764 |
| P04004 | -1.3605995 | 0.1939297 | 9.270800 | -7.015941 | 0.0000536 | 0.0039063 | P04004 |
| P24844 | -1.6335444 | 0.2377501 | 9.433933 | -6.870845 | 0.0000580 | 0.0040359 | P24844 |
| P11586 | 1.4562651 | 0.2117089 | 9.333226 | 6.878620 | 0.0000606 | 0.0040359 | P11586 |
| Q5NDL2 | -1.9157423 | 0.2823635 | 9.517072 | -6.784667 | 0.0000615 | 0.0040359 | Q5NDL2 |
| P60468 | -1.4985317 | 0.2011269 | 8.191586 | -7.450677 | 0.0000642 | 0.0040359 | P60468 |
| Q69YU5 | 2.4754644 | 0.3685265 | 9.579396 | 6.717195 | 0.0000646 | 0.0040359 | Q69YU5 |
| Q9BW30 | -1.9177197 | 0.2869707 | 9.534123 | -6.682633 | 0.0000688 | 0.0041828 | Q9BW30 |
| Q15113 | -1.6629972 | 0.2516710 | 9.536113 | -6.607821 | 0.0000752 | 0.0043619 | Q15113 |
| P04196 | -1.2482839 | 0.1860851 | 9.273169 | -6.708133 | 0.0000762 | 0.0043619 | P04196 |
| Q9Y4W6 | 1.0879384 | 0.1622163 | 9.235088 | 6.706716 | 0.0000778 | 0.0043619 | Q9Y4W6 |
| P19429 | 2.2476195 | 0.3448005 | 9.586884 | 6.518608 | 0.0000818 | 0.0043619 | P19429 |
| P02747 | -1.4838172 | 0.2247118 | 9.364965 | -6.603201 | 0.0000823 | 0.0043619 | P02747 |
| P02775 | -1.5738214 | 0.2400296 | 9.442684 | -6.556779 | 0.0000837 | 0.0043619 | P02775 |
| Q9UGT4 | -1.7582895 | 0.2716919 | 9.601092 | -6.471630 | 0.0000861 | 0.0043791 | Q9UGT4 |
| P02743 | -1.4372727 | 0.2184192 | 9.259904 | -6.580340 | 0.0000891 | 0.0044302 | P02743 |
| Q9NRG4 | 2.4292862 | 0.3537262 | 8.484155 | 6.867703 | 0.0000974 | 0.0047344 | Q9NRG4 |
| Q06828 | -3.2878219 | 0.5231368 | 9.730028 | -6.284823 | 0.0001024 | 0.0048709 | Q06828 |
| P01031 | -1.0556049 | 0.1655342 | 9.289894 | -6.376960 | 0.0001120 | 0.0052117 | P01031 |
| Q9HCB6 | -1.5477618 | 0.2477605 | 9.478445 | -6.247007 | 0.0001203 | 0.0054690 | Q9HCB6 |
| P05997 | -1.9099570 | 0.3080473 | 9.559204 | -6.200206 | 0.0001230 | 0.0054690 | P05997 |
| P02452 | -1.6021991 | 0.2593204 | 9.585356 | -6.178453 | 0.0001250 | 0.0054690 | P02452 |
| P48681 | -1.0102767 | 0.1617208 | 9.238145 | -6.247042 | 0.0001343 | 0.0057622 | P48681 |
| O14967 | -1.2432881 | 0.2005888 | 9.248331 | -6.198193 | 0.0001419 | 0.0059021 | O14967 |
| O00180 | -3.4637187 | 0.5425840 | 8.732659 | -6.383747 | 0.0001457 | 0.0059021 | O00180 |
| P23142 | -1.8311086 | 0.3022843 | 9.545973 | -6.057572 | 0.0001483 | 0.0059021 | P23142 |
| Q9HAT2 | 1.7914105 | 0.2921487 | 9.296680 | 6.131845 | 0.0001507 | 0.0059021 | Q9HAT2 |
| P10109 | 1.1498726 | 0.1893963 | 9.462988 | 6.071252 | 0.0001511 | 0.0059021 | P10109 |
| Q13011 | 1.1833804 | 0.1965056 | 9.478440 | 6.022121 | 0.0001597 | 0.0061310 | Q13011 |
| Q8N142 | 1.2230990 | 0.2045058 | 9.488674 | 5.980754 | 0.0001677 | 0.0063249 | Q8N142 |
| Q9UNW9 | 3.0434487 | 0.5128825 | 9.536696 | 5.934007 | 0.0001745 | 0.0063613 | Q9UNW9 |
| Q9NRX4 | 1.5004765 | 0.2535304 | 9.576287 | 5.918329 | 0.0001752 | 0.0063613 | Q9NRX4 |
| A6NMZ7 | -1.9793762 | 0.3373225 | 9.707078 | -5.867904 | 0.0001773 | 0.0063613 | A6NMZ7 |
| P23786 | 0.9013183 | 0.1492546 | 9.134748 | 6.038796 | 0.0001818 | 0.0064157 | P23786 |
| Q04760 | 1.5360653 | 0.2602426 | 9.441126 | 5.902435 | 0.0001892 | 0.0064537 | Q04760 |
| Q15327 | -1.2106705 | 0.2054754 | 9.451901 | -5.892044 | 0.0001909 | 0.0064537 | Q15327 |
| P17540 | 1.0681187 | 0.1809634 | 9.408560 | 5.902403 | 0.0001918 | 0.0064537 | P17540 |
| O95865 | -1.1476181 | 0.1943037 | 9.360986 | -5.906311 | 0.0001947 | 0.0064537 | O95865 |
| Q5JPH6 | 3.4628551 | 0.4565052 | 6.397711 | 7.585577 | 0.0002001 | 0.0065352 | Q5JPH6 |
| P51884 | -1.3320008 | 0.2297628 | 9.576049 | -5.797287 | 0.0002052 | 0.0066034 | P51884 |
| P04083 | -0.9538541 | 0.1644374 | 9.318065 | -5.800712 | 0.0002269 | 0.0071964 | P04083 |
| P30711 | -1.3399014 | 0.2344998 | 9.492387 | -5.713869 | 0.0002368 | 0.0073379 | P30711 |
| Q7L4S7 | -1.7163672 | 0.2582743 | 7.332929 | -6.645522 | 0.0002381 | 0.0073379 | Q7L4S7 |
| O95980 | -1.3087089 | 0.2312413 | 9.498408 | -5.659495 | 0.0002539 | 0.0077157 | O95980 |
| P00325 | -1.1271284 | 0.1975885 | 9.177945 | -5.704422 | 0.0002721 | 0.0081541 | P00325 |
| Q9UKS6 | 1.1555353 | 0.2067472 | 9.488160 | 5.589122 | 0.0002799 | 0.0081958 | Q9UKS6 |
| P28066 | -1.1657717 | 0.2083507 | 9.457629 | -5.595237 | 0.0002809 | 0.0081958 | P28066 |
| Q9ULD0 | -1.6081853 | 0.2436750 | 7.104538 | -6.599713 | 0.0002855 | 0.0082204 | Q9ULD0 |
| Q86VU5 | 1.3909551 | 0.2522544 | 9.638787 | 5.514095 | 0.0002927 | 0.0083166 | Q86VU5 |
| P14923 | 0.8397640 | 0.1494538 | 9.171357 | 5.618887 | 0.0003046 | 0.0085450 | P14923 |
| Q6PCB0 | -1.3159366 | 0.2380883 | 9.378729 | -5.527094 | 0.0003170 | 0.0087809 | Q6PCB0 |
| P24311 | 1.3296314 | 0.2409955 | 9.362276 | 5.517246 | 0.0003232 | 0.0088407 | P24311 |
| Q9HBL0 | 1.3884913 | 0.2368572 | 8.180895 | 5.862145 | 0.0003467 | 0.0092101 | Q9HBL0 |
| Q9BXV9 | 1.4577749 | 0.2727782 | 9.805041 | 5.344177 | 0.0003488 | 0.0092101 | Q9BXV9 |
| Q9ULL5-3 | -1.7449314 | 0.3044597 | 8.505757 | -5.731239 | 0.0003494 | 0.0092101 | Q9ULL5-3 |
| P61925 | 1.5601183 | 0.2689974 | 8.266540 | 5.799751 | 0.0003583 | 0.0093340 | P61925 |
| P23083 | -2.6793814 | 0.4331242 | 7.380951 | -6.186173 | 0.0003652 | 0.0094013 | P23083 |
| O75489 | 0.9977662 | 0.1872393 | 9.598971 | 5.328829 | 0.0003829 | 0.0096301 | O75489 |
| P63316 | 0.9567764 | 0.1785086 | 9.478611 | 5.359834 | 0.0003829 | 0.0096301 | P63316 |
| P07195 | 0.9985697 | 0.1874549 | 9.501868 | 5.326987 | 0.0003972 | 0.0098767 | P07195 |
| P35625 | -2.1754244 | 0.3893925 | 8.562007 | -5.586713 | 0.0004068 | 0.0100014 | P35625 |
| P17174 | 1.0116885 | 0.1913267 | 9.468860 | 5.287755 | 0.0004242 | 0.0103116 | P17174 |
| O15230 | -0.8483405 | 0.1605308 | 9.335882 | -5.284596 | 0.0004465 | 0.0107248 | O15230 |
| Q6PI78 | 1.4696344 | 0.2848643 | 9.822092 | 5.159069 | 0.0004510 | 0.0107248 | Q6PI78 |
| Q9BXN1 | -1.6449225 | 0.3195425 | 9.779246 | -5.147743 | 0.0004648 | 0.0109342 | Q9BXN1 |
| Q9Y6X5 | -0.9114382 | 0.1743822 | 9.378833 | -5.226669 | 0.0004760 | 0.0110806 | Q9Y6X5 |
| Q16647 | -1.3098697 | 0.2578596 | 9.742336 | -5.079778 | 0.0005184 | 0.0119394 | Q16647 |
| P21399 | 0.7733919 | 0.1506412 | 9.280176 | 5.134001 | 0.0005594 | 0.0127385 | P21399 |
| P51970 | 0.8453891 | 0.1662355 | 9.453305 | 5.085491 | 0.0005647 | 0.0127385 | P51970 |
| Q96RP7 | -3.2449509 | 0.4617082 | 5.483644 | -7.028142 | 0.0006117 | 0.0136580 | Q96RP7 |
| Q9Y3B4 | -0.8676537 | 0.1727639 | 9.303225 | -5.022194 | 0.0006482 | 0.0143256 | Q9Y3B4 |
| P50453 | -0.7669119 | 0.1527314 | 9.251199 | -5.021311 | 0.0006602 | 0.0144443 | P50453 |
| Q6DKK2 | 1.0463979 | 0.2120923 | 9.412715 | 4.933692 | 0.0007089 | 0.0153565 | Q6DKK2 |
| P02748 | -0.9028985 | 0.1827215 | 9.328466 | -4.941392 | 0.0007201 | 0.0154467 | P02748 |
| Q8TBQ9 | -1.2020325 | 0.2459524 | 9.446801 | -4.887257 | 0.0007494 | 0.0159192 | Q8TBQ9 |
| Q9NZ01 | -1.2126719 | 0.2534197 | 9.896186 | -4.785231 | 0.0007618 | 0.0160279 | Q9NZ01 |
| P12110 | -0.9713556 | 0.2007269 | 9.536991 | -4.839189 | 0.0007814 | 0.0161672 | P12110 |
| P12814 | -1.3411812 | 0.2670430 | 8.741139 | -5.022341 | 0.0007832 | 0.0161672 | P12814 |
| P04003 | -1.0633338 | 0.2197570 | 9.469818 | -4.838681 | 0.0007979 | 0.0163158 | P04003 |
| Q53FA7 | 1.5581378 | 0.3239189 | 9.564359 | 4.810272 | 0.0008082 | 0.0163742 | Q53FA7 |
| P00748 | -1.1346342 | 0.2388519 | 9.766668 | -4.750367 | 0.0008324 | 0.0167096 | P00748 |
| P14550 | -0.7790248 | 0.1630649 | 9.485559 | -4.777390 | 0.0008677 | 0.0171682 | P14550 |
| Q9UBB5 | 1.4018949 | 0.2313680 | 6.082236 | 6.059156 | 0.0008710 | 0.0171682 | Q9UBB5 |
| P11766 | 0.7921470 | 0.1663652 | 9.467043 | 4.761494 | 0.0008928 | 0.0172923 | P11766 |
| P06732 | 0.7828169 | 0.1641535 | 9.430106 | 4.768811 | 0.0008931 | 0.0172923 | P06732 |
| Q12996 | -1.1900567 | 0.2231950 | 7.365790 | -5.331914 | 0.0009195 | 0.0176483 | Q12996 |
| Q8TDB4 | -1.8274152 | 0.3415970 | 7.269123 | -5.349622 | 0.0009413 | 0.0178003 | Q8TDB4 |
| P36021 | -1.7395850 | 0.3577586 | 8.828176 | -4.862455 | 0.0009437 | 0.0178003 | P36021 |
| Q92604 | -1.3127130 | 0.2837564 | 9.947381 | -4.626197 | 0.0009548 | 0.0178558 | Q92604 |
| Q9Y3D0 | 1.6486483 | 0.2959909 | 6.670659 | 5.569929 | 0.0009933 | 0.0184189 | Q9Y3D0 |
| Q6P1L8 | 0.8425184 | 0.1817397 | 9.707064 | 4.635853 | 0.0010038 | 0.0184563 | Q6P1L8 |
| Q6UWS5 | 1.7220515 | 0.3040600 | 6.427167 | 5.663526 | 0.0010290 | 0.0186969 | Q6UWS5 |
| Q6SZW1 | -1.4203348 | 0.2792520 | 7.758278 | -5.086212 | 0.0010392 | 0.0186969 | Q6SZW1 |
| P51151 | 0.7775244 | 0.1671543 | 9.434716 | 4.651537 | 0.0010578 | 0.0186969 | P51151 |
| Q53GQ0 | -1.1175142 | 0.2430407 | 9.718619 | -4.598054 | 0.0010590 | 0.0186969 | Q53GQ0 |
| P30405 | -1.0553674 | 0.2310692 | 9.892316 | -4.567322 | 0.0010596 | 0.0186969 | P30405 |
| P36955 | -1.0735843 | 0.2345867 | 9.772134 | -4.576493 | 0.0010784 | 0.0187156 | P36955 |
| P35754 | 1.0604547 | 0.2323092 | 9.831307 | 4.564842 | 0.0010807 | 0.0187156 | P35754 |
| Q14195-2 | -1.5280180 | 0.3350901 | 9.839393 | -4.560022 | 0.0010863 | 0.0187156 | Q14195-2 |
| Q5VUM1 | 0.9061256 | 0.1979080 | 9.589831 | 4.578519 | 0.0011288 | 0.0192961 | Q5VUM1 |
| P13667 | -0.7220582 | 0.1596332 | 9.557580 | -4.523233 | 0.0012366 | 0.0209741 | P13667 |
| Q9NQ50 | 0.8058197 | 0.1789252 | 9.618824 | 4.503668 | 0.0012531 | 0.0209972 | Q9NQ50 |
| Q00688 | 0.8160471 | 0.1814802 | 9.643216 | 4.496617 | 0.0012584 | 0.0209972 | Q00688 |
| O95182 | 0.8368612 | 0.1862421 | 9.636518 | 4.493405 | 0.0012667 | 0.0209972 | O95182 |
| Q8WZ42-6 | 0.6975568 | 0.1542241 | 9.391830 | 4.523007 | 0.0012931 | 0.0212722 | Q8WZ42-6 |
| Q9ULC3 | -0.8541539 | 0.1918910 | 9.768835 | -4.451245 | 0.0013056 | 0.0213180 | Q9ULC3 |
| O94919 | -0.6975347 | 0.1543245 | 9.271008 | -4.519921 | 0.0013422 | 0.0215226 | O94919 |
| Q9UKX3 | 1.2122113 | 0.2751758 | 9.937136 | 4.405225 | 0.0013445 | 0.0215226 | Q9UKX3 |
| P46060 | -1.2255778 | 0.2663746 | 8.847600 | -4.600957 | 0.0013476 | 0.0215226 | P46060 |
| Q86VP6 | -0.8480596 | 0.1934764 | 9.783783 | -4.383271 | 0.0014437 | 0.0228894 | Q86VP6 |
| P80723 | -1.1832701 | 0.2565319 | 8.478989 | -4.612565 | 0.0014826 | 0.0231809 | P80723 |
| P13073 | 0.7406291 | 0.1679121 | 9.498815 | 4.410813 | 0.0014863 | 0.0231809 | P13073 |
| Q63HM9 | 0.8199517 | 0.1857191 | 9.454228 | 4.415009 | 0.0014938 | 0.0231809 | Q63HM9 |
| Q5M9N0 | -1.6991316 | 0.3824461 | 9.175048 | -4.442800 | 0.0015423 | 0.0235916 | Q5M9N0 |
| P25940 | -0.9714255 | 0.2245491 | 9.837648 | -4.326117 | 0.0015568 | 0.0235916 | P25940 |
| O14949 | 1.0203567 | 0.2356108 | 9.770618 | 4.330688 | 0.0015706 | 0.0235916 | O14949 |
| Q5T481 | 0.7543759 | 0.1728985 | 9.531949 | 4.363114 | 0.0015840 | 0.0235916 | Q5T481 |
| Q5JUQ0 | 2.3923426 | 0.5129180 | 8.057125 | 4.664182 | 0.0015843 | 0.0235916 | Q5JUQ0 |
| Q12988 | -0.7197658 | 0.1648005 | 9.502808 | -4.367499 | 0.0015850 | 0.0235916 | Q12988 |
| P14543 | -0.8237268 | 0.1917450 | 9.883607 | -4.295950 | 0.0016142 | 0.0238635 | P14543 |
| P15848 | 0.9610948 | 0.2235365 | 9.748276 | 4.299497 | 0.0016569 | 0.0242835 | P15848 |
| P48047 | 0.7986239 | 0.1848261 | 9.569504 | 4.320948 | 0.0016733 | 0.0242835 | P48047 |
| P35052 | -0.9094996 | 0.2011858 | 8.489597 | -4.520695 | 0.0016759 | 0.0242835 | P35052 |
| P54296 | 0.6696406 | 0.1553053 | 9.514121 | 4.311768 | 0.0017199 | 0.0247578 | P54296 |
| Q15274 | -1.2921878 | 0.2941256 | 9.004136 | -4.393319 | 0.0017352 | 0.0247789 | Q15274 |
| O60503 | 1.4353510 | 0.2857061 | 6.681999 | 5.023872 | 0.0017484 | 0.0247789 | O60503 |
| P01034 | -0.9479850 | 0.2241187 | 9.971490 | -4.229835 | 0.0017554 | 0.0247789 | P01034 |
| Q96H79 | -1.4874612 | 0.2966075 | 6.634593 | -5.014914 | 0.0018028 | 0.0251508 | Q96H79 |
| O14980 | -0.6307124 | 0.1452780 | 9.144414 | -4.341416 | 0.0018047 | 0.0251508 | O14980 |
| Q9BUF5 | -1.0681765 | 0.2531304 | 9.885958 | -4.219867 | 0.0018176 | 0.0251700 | Q9BUF5 |
| P07585 | -1.3970312 | 0.3326320 | 9.953888 | -4.199930 | 0.0018475 | 0.0253056 | P07585 |
| P01042 | -1.8796814 | 0.4047966 | 7.668959 | -4.643520 | 0.0018550 | 0.0253056 | P01042 |
| P24752 | 0.8147048 | 0.1944004 | 9.964493 | 4.190859 | 0.0018699 | 0.0253056 | P24752 |
| Q8WY22 | -0.9915506 | 0.2269833 | 8.852505 | -4.368386 | 0.0018736 | 0.0253056 | Q8WY22 |
| Q86SX6 | 0.7916631 | 0.1879923 | 9.736249 | 4.211146 | 0.0019058 | 0.0255827 | Q86SX6 |
| Q86WV6 | -0.8075576 | 0.1910670 | 9.427466 | -4.226569 | 0.0019992 | 0.0264446 | Q86WV6 |
| Q9H479 | 0.7577083 | 0.1810834 | 9.704367 | 4.184305 | 0.0020016 | 0.0264446 | Q9H479 |
| Q53GG5 | 1.1080565 | 0.2648156 | 9.694276 | 4.184258 | 0.0020063 | 0.0264446 | Q53GG5 |
| Q9BTV4 | -0.9341181 | 0.2278205 | 10.185239 | -4.100238 | 0.0020631 | 0.0270307 | Q9BTV4 |
| Q9NNX1 | 2.9099745 | 0.6201504 | 7.088545 | 4.692369 | 0.0021547 | 0.0280621 | Q9NNX1 |
| P09619 | -0.6550082 | 0.1570063 | 9.413215 | -4.171860 | 0.0021806 | 0.0282314 | P09619 |
| Q8WWA0 | -2.7659862 | 0.6806045 | 10.156219 | -4.064014 | 0.0022007 | 0.0283248 | Q8WWA0 |
| P49770 | 0.8269399 | 0.2038694 | 9.944656 | 4.056224 | 0.0023268 | 0.0295944 | P49770 |
| Q02127 | 1.2039706 | 0.2657171 | 7.401140 | 4.531024 | 0.0023416 | 0.0295944 | Q02127 |
| I3L505 | 1.1067201 | 0.2753159 | 10.197875 | 4.019819 | 0.0023451 | 0.0295944 | I3L505 |
| Q9H3K6 | 0.6971910 | 0.1711668 | 9.728454 | 4.073168 | 0.0023699 | 0.0295944 | Q9H3K6 |
| P01024 | -0.6372280 | 0.1551230 | 9.468507 | -4.107887 | 0.0023758 | 0.0295944 | P01024 |
| O43920 | 0.7719300 | 0.1911945 | 9.980424 | 4.037406 | 0.0023805 | 0.0295944 | O43920 |
| P02461 | -1.9014625 | 0.4756591 | 10.174961 | -3.997532 | 0.0024428 | 0.0301970 | P02461 |
| P31930 | 0.6341469 | 0.1559075 | 9.566010 | 4.067457 | 0.0024760 | 0.0304356 | P31930 |
| Q13541 | 1.0054699 | 0.2514700 | 10.012338 | 3.998369 | 0.0025188 | 0.0305275 | Q13541 |
| Q9NQR4 | 0.8497236 | 0.2125583 | 10.005294 | 3.997603 | 0.0025254 | 0.0305275 | Q9NQR4 |
| Q9Y287 | -0.8805657 | 0.2201911 | 9.991693 | -3.999097 | 0.0025262 | 0.0305275 | Q9Y287 |
| P06727 | -0.7439890 | 0.1815376 | 9.225409 | -4.098264 | 0.0025471 | 0.0305275 | P06727 |
| P00352 | -0.6833984 | 0.1679840 | 9.400007 | -4.068236 | 0.0025644 | 0.0305275 | P00352 |
| P40939 | 0.6064551 | 0.1482708 | 9.244856 | 4.090186 | 0.0025672 | 0.0305275 | P40939 |
| P55039 | 1.0233844 | 0.2291242 | 7.304575 | 4.466505 | 0.0026220 | 0.0310109 | P55039 |
| Q04721 | 1.0485452 | 0.2622467 | 9.688477 | 3.998316 | 0.0026896 | 0.0315505 | Q04721 |
| P49458 | -1.1981452 | 0.2798019 | 7.977794 | -4.282120 | 0.0026970 | 0.0315505 | P49458 |
| P04209 | 0.8634678 | 0.2148474 | 9.495921 | 4.018982 | 0.0027109 | 0.0315505 | P04209 |
| Q15773 | 0.7582360 | 0.1916223 | 9.910180 | 3.956931 | 0.0027477 | 0.0316513 | Q15773 |
| P02790 | -0.7830751 | 0.1991261 | 10.113121 | -3.932558 | 0.0027485 | 0.0316513 | P02790 |
| P07451 | -0.7379038 | 0.1847289 | 9.585814 | -3.994523 | 0.0027639 | 0.0316617 | P07451 |
| Q53T59 | -1.1978861 | 0.2885746 | 8.466573 | -4.151045 | 0.0028322 | 0.0322757 | Q53T59 |
| P03928 | 0.7362835 | 0.1874644 | 9.915745 | 3.927591 | 0.0028776 | 0.0326230 | P03928 |
| Q9UBG0 | -1.0333426 | 0.2624451 | 9.768266 | -3.937366 | 0.0029158 | 0.0328547 | Q9UBG0 |
| Q96MM6 | 1.3370336 | 0.3311082 | 9.013572 | 4.038057 | 0.0029281 | 0.0328547 | Q96MM6 |
| Q9UMR3 | -1.2814546 | 0.2782321 | 6.538023 | -4.605703 | 0.0029441 | 0.0328657 | Q9UMR3 |
| Q92681 | -1.0478169 | 0.2621030 | 9.184710 | -3.997730 | 0.0029961 | 0.0331615 | Q92681 |
| Q02318 | -1.0543306 | 0.2224723 | 6.136433 | -4.739155 | 0.0030083 | 0.0331615 | Q02318 |
| Q9BX66-5 | 1.0070024 | 0.2303104 | 7.236228 | 4.372370 | 0.0030161 | 0.0331615 | Q9BX66-5 |
| O60760 | -1.4579900 | 0.3648196 | 9.077881 | -3.996469 | 0.0030733 | 0.0335841 | O60760 |
| Q14353 | 0.9837112 | 0.2560148 | 10.277210 | 3.842400 | 0.0030937 | 0.0335841 | Q14353 |
| O76031 | 0.5944195 | 0.1511239 | 9.488222 | 3.933326 | 0.0031046 | 0.0335841 | O76031 |
| P21953 | 0.9232656 | 0.2355721 | 9.579770 | 3.919248 | 0.0031159 | 0.0335841 | P21953 |
| P17050 | -0.6604019 | 0.1688233 | 9.576790 | -3.911793 | 0.0031547 | 0.0338359 | P17050 |
| O00264 | -0.7449556 | 0.1928619 | 9.921595 | -3.862637 | 0.0031930 | 0.0339604 | O00264 |
| P13671 | -0.8057348 | 0.2080950 | 9.834309 | -3.871957 | 0.0031974 | 0.0339604 | P13671 |
| P08574 | 0.6109407 | 0.1574461 | 9.718140 | 3.880317 | 0.0032258 | 0.0340964 | P08574 |
| Q8IUX7 | -1.7161917 | 0.4188348 | 8.138665 | -4.097538 | 0.0033255 | 0.0349822 | Q8IUX7 |
| Q96CS3 | -0.7036507 | 0.1837872 | 9.754773 | -3.828616 | 0.0034805 | 0.0364366 | Q96CS3 |
| Q9BZH6 | 1.9481367 | 0.5201485 | 10.412295 | 3.745347 | 0.0035553 | 0.0368470 | Q9BZH6 |
| P28070 | -0.6488737 | 0.1693730 | 9.617848 | -3.831034 | 0.0035579 | 0.0368470 | P28070 |
| Q3ZCW2 | -0.8754815 | 0.2241369 | 9.021266 | -3.906013 | 0.0035702 | 0.0368470 | Q3ZCW2 |
| P09874 | 0.5848364 | 0.1521501 | 9.439573 | 3.843813 | 0.0036089 | 0.0370716 | P09874 |
| Q9UBV8 | -0.7235789 | 0.1896245 | 9.594672 | -3.815851 | 0.0036613 | 0.0372603 | Q9UBV8 |
| Q8WZA9 | -0.6588659 | 0.1724436 | 9.553531 | -3.820763 | 0.0036613 | 0.0372603 | Q8WZA9 |
| P40261 | -0.9050994 | 0.2361125 | 9.424468 | -3.833340 | 0.0036798 | 0.0372752 | P40261 |
| Q16762 | 0.6896826 | 0.1829052 | 9.857793 | 3.770710 | 0.0037509 | 0.0376724 | Q16762 |
| O15195-2 | 1.3363469 | 0.3118800 | 6.902306 | 4.284811 | 0.0037535 | 0.0376724 | O15195-2 |
| Q9HAN9 | 1.1414801 | 0.2876745 | 8.335372 | 3.967958 | 0.0038043 | 0.0380082 | Q9HAN9 |
| Q8TBP6 | -0.8031089 | 0.2158104 | 10.178944 | -3.721363 | 0.0038477 | 0.0382674 | Q8TBP6 |
| Q07507 | -0.7241081 | 0.1920710 | 9.608284 | -3.770002 | 0.0039297 | 0.0389061 | Q07507 |
| P46940 | -0.6392674 | 0.1713924 | 9.877120 | -3.729847 | 0.0039957 | 0.0393808 | P46940 |
| O95202 | 0.5779418 | 0.1532531 | 9.434554 | 3.771159 | 0.0040519 | 0.0396103 | O95202 |
| P08603 | -0.6992781 | 0.1878961 | 9.869474 | -3.721621 | 0.0040552 | 0.0396103 | P08603 |
| Q8TAL6 | -1.8063108 | 0.4072295 | 6.166509 | -4.435608 | 0.0041152 | 0.0400182 | Q8TAL6 |
| Q9HB40 | -1.1127203 | 0.2527625 | 6.220567 | -4.402237 | 0.0041808 | 0.0404764 | Q9HB40 |
| O75190-3 | 1.1109397 | 0.3052132 | 10.314084 | 3.639881 | 0.0043145 | 0.0415862 | O75190-3 |
| Q9H511 | 0.6668969 | 0.1811347 | 9.812109 | 3.681773 | 0.0043711 | 0.0419470 | Q9H511 |
| Q07954 | -0.6207211 | 0.1703226 | 9.863946 | -3.644385 | 0.0046065 | 0.0440134 | Q07954 |
| Q9NQZ5 | 1.1063978 | 0.3078097 | 10.264418 | 3.594421 | 0.0046943 | 0.0446157 | Q9NQZ5 |
| Q16654 | 0.8623740 | 0.2320437 | 9.094702 | 3.716429 | 0.0047103 | 0.0446157 | Q16654 |
| Q2TAA5 | -0.6977539 | 0.1932119 | 10.009057 | -3.611340 | 0.0047506 | 0.0448030 | Q2TAA5 |
| Q5JVS0 | -1.3591318 | 0.2824461 | 5.020511 | -4.812004 | 0.0047804 | 0.0448910 | Q5JVS0 |
| Q0VAK6 | 0.9271117 | 0.2605769 | 10.498467 | 3.557919 | 0.0048217 | 0.0450849 | Q0VAK6 |
| P07686 | 0.8405364 | 0.2229746 | 8.526947 | 3.769651 | 0.0048703 | 0.0450865 | P07686 |
| Q13636 | -1.5458451 | 0.3698208 | 6.499442 | -4.179984 | 0.0048744 | 0.0450865 | Q13636 |
| P15374 | 0.7806300 | 0.2186997 | 10.281794 | 3.569416 | 0.0048837 | 0.0450865 | P15374 |
| P78406 | -1.1054909 | 0.2599367 | 6.222935 | -4.252923 | 0.0049379 | 0.0452520 | P78406 |
| P20774 | -1.0939518 | 0.3086286 | 10.484917 | -3.544558 | 0.0049430 | 0.0452520 | P20774 |
| Q08945 | -0.8371286 | 0.2282277 | 9.153856 | -3.667954 | 0.0050247 | 0.0458089 | Q08945 |
| Q99766 | 0.5801784 | 0.1601546 | 9.531547 | 3.622615 | 0.0050489 | 0.0458380 | Q99766 |
| P49207 | -0.5839141 | 0.1637478 | 10.075594 | -3.565936 | 0.0050702 | 0.0458413 | P49207 |
| P22695 | 0.6160228 | 0.1729941 | 10.018999 | 3.560947 | 0.0051578 | 0.0464413 | P22695 |
| Q9UI09 | 0.6403409 | 0.1794697 | 9.918617 | 3.567961 | 0.0051791 | 0.0464419 | Q9UI09 |
| P07357 | -0.6143868 | 0.1718693 | 9.780942 | -3.574733 | 0.0052357 | 0.0467581 | P07357 |
| Q16082 | -0.6322050 | 0.1787586 | 10.109135 | -3.536641 | 0.0052977 | 0.0469738 | Q16082 |
| Q8IXM3 | 0.6461790 | 0.1818011 | 9.886801 | 3.554318 | 0.0053241 | 0.0469738 | Q8IXM3 |
| Q92901 | 0.7836579 | 0.2227719 | 10.288945 | 3.517759 | 0.0053243 | 0.0469738 | Q92901 |
| Q13825 | 1.1245424 | 0.3221135 | 10.534211 | 3.491137 | 0.0053793 | 0.0472691 | Q13825 |
| Q9NQT8 | -1.1513781 | 0.2915578 | 7.066202 | -3.949056 | 0.0054352 | 0.0472891 | Q9NQT8 |
| P01604 | -1.2896968 | 0.2795691 | 5.116835 | -4.613159 | 0.0054481 | 0.0472891 | P01604 |
| Q6ZVF9 | -1.0955862 | 0.2709835 | 6.656492 | -4.042999 | 0.0054588 | 0.0472891 | Q6ZVF9 |
| P01699 | -1.6297466 | 0.3943727 | 6.325570 | -4.132503 | 0.0054681 | 0.0472891 | P01699 |
| Q16795 | 0.6450332 | 0.1840663 | 10.157955 | 3.504353 | 0.0055524 | 0.0478297 | Q16795 |
| Q9UI47 | 0.5900888 | 0.1676449 | 9.800459 | 3.519874 | 0.0057127 | 0.0490175 | Q9UI47 |
| O75947 | 0.6002336 | 0.1718265 | 10.023771 | 3.493253 | 0.0057709 | 0.0492302 | O75947 |
| P62760 | -0.9670022 | 0.2804990 | 10.519281 | -3.447436 | 0.0058116 | 0.0492302 | P62760 |
| Q04446 | 0.8608184 | 0.2481309 | 10.234155 | 3.469211 | 0.0058272 | 0.0492302 | Q04446 |
| Q9BSD7 | 1.4315921 | 0.3832730 | 7.936523 | 3.735176 | 0.0058275 | 0.0492302 | Q9BSD7 |
| Q9HC36 | 0.9665091 | 0.2423551 | 6.638088 | 3.987987 | 0.0058727 | 0.0494208 | Q9HC36 |
| P11182 | 0.5859546 | 0.1675892 | 9.821787 | 3.496374 | 0.0059193 | 0.0495347 | P11182 |
| O15118 | -1.3330724 | 0.3463625 | 7.225517 | -3.848778 | 0.0059315 | 0.0495347 | O15118 |
| Q9UHP9 | 0.7222478 | 0.2074836 | 9.910771 | 3.480988 | 0.0059908 | 0.0497354 | Q9UHP9 |
| Q96JM3 | -0.9006783 | 0.2426905 | 7.958417 | -3.711222 | 0.0060010 | 0.0497354 | Q96JM3 |
6.7.8 Interaction
Let us retrieve the result table from the rowData. The second column contains the results for the interaction contrast.
inferenceInt <- rowData(pe[["proteins"]])[[colnames(L)[4]]]
inferenceInt$Protein <- rownames(inferenceInt)
head(inferenceInt) logFC se df t pval adjPval Protein
A0PJW6 0.00000000 7.792300e-10 14.003000 0.0000000 1.0000000 1 A0PJW6
A0PJZ3 NA NA NA NA NA NA A0PJZ3
A0PK00 NA NA 5.826529 NA NA NA A0PK00
A1A4S6 0.01527264 1.258090e-01 13.324734 0.1213955 0.9051894 1 A1A4S6
A1A5D9 NA NA NA NA NA NA A1A5D9
A1IGU5 -0.28917988 2.871906e-01 10.934858 -1.0069267 0.3357322 1 A1IGU5Volcano plot
Volcano plots are straightforward to generate from the inference table above. We also use ggrepel to annotate the 20 most significant proteins.
ggplot(inferenceInt) +
aes(x = logFC, y = -log10(pval), color = adjPval < 0.05) +
geom_point() +
geom_text_repel(data = slice_min(inferenceInt, adjPval, n = 20),
aes(label = Protein)) +
scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
ggtitle("log2 FC V-A Right",
paste("Hypothesis test:", colnames(L)[2], "= 0"))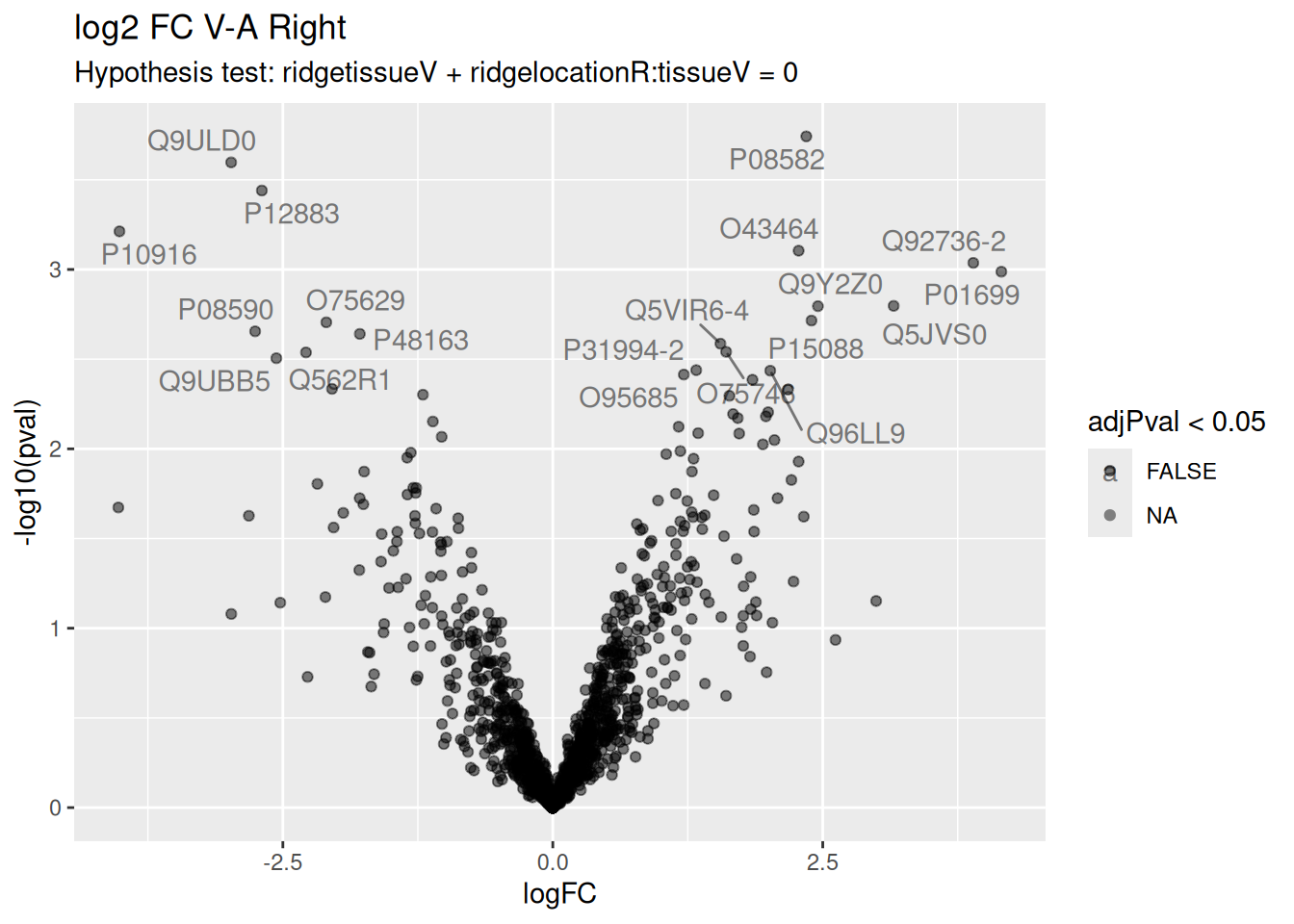
As there are no significant features, we do not return a top table and do not make a heatmap for this contrast.
6.8 Conclusion
In this chapter, we illustrated the analysis of a label-free proteomics data set with technical replication. We followed the workflow described in the previous chapters with minimal changes.
The experiment presented in this chapter presents a complex design and is an excellent illustration on how to model data with main effects, interactions and block effects. We could investigate:
- The difference in protein abundance between the atrium and ventriculum in the left heart compartment.
- The difference in protein abundance between the atrium and ventriculum in the right heart compartment.
- The difference in protein abundance between the atrium and ventriculum, averaged over the right and left heart compartment.
- The interaction, whether the difference between atrium and ventriculum is affected by whether we focus on the left heart or the right heart compartment.
Note that we use the same heatmap annotations so we don’t need to generate it again.↩︎
