Hoofdstuk 1 Inleiding
De meeste vragen in de levenswetenschappen kunnen slechts beantwoord worden door gegevens te verzamelen en te analyseren, bijvoorbeeld:
- Voor welke genen verschilt het expressieniveau in kanker en normaal weefsel?
- Hoe snel lopen kangoeroes?
- Wat is de invloed van regelmatig joggen op bloeddruk?
- Is er een relatie tussen zweetgeur en de samenstelling van de microbiële gemeenschap onder de oksel?
Bij onderzoek naar biologische processen moet men zich realiseren dat uitkomsten aan variatie onderhevig zijn. Aspirine is bijvoorbeeld niet bij iedereen even effectief om hoofdpijn te verzachten zodat de uitkomst voor een persoon met en zonder inname van aspirine meestal niet exact te voorspellen valt. Dit wordt mede veroorzaakt door het feit dat mensen verschillen in gewicht, ziektegraad, gevoeligheid voor een stof, … Bovendien reageert een persoon vaak anders op een stof naargelang hij moe of uitgerust is, het middel ’s morgens of ‘s avonds inneemt, voor of na het eten, op geregelde tijdstippen of met onregelmatige intervallen, … En zelfs al mocht een bepaalde stof voor iedereen even effectief zijn, dan nog is het zo dat verschillende metingen voor een zelfde persoon zelden gelijk. De aanwezigheid van die biologische variabiliteit is bijzonder opvallend in de context van roken: de schadelijke gevolgen van roken op longkanker en hartaandoeningen zijn intussen goed gekend, maar nagenoeg iedereen kent wel iemand die gans zijn leven gerookt heeft en desondanks meer dan 80 jaar oud geworden is.
Precies omwille van die biologische variabiliteit is het moeilijk om wetenschappelijke vragen goed te beantwoorden en zal men zelden onmiddellijk het antwoord zien na het bekijken van ruwe gegevens. Onderzoekers in de fysiologie, bijvoorbeeld, gaan vaak na wat het effect is van een bepaalde substantie (bijvoorbeeld, een geneesmiddel, hormoon of toxine) op experimentele dieren (bijvoorbeeld, ratten of ook in vitro weefselpreparaten). Dit effect wordt bestudeerd door verschillen in respons te meten tussen dieren geïnjecteerd met de substantie en controledieren die werden geïnjecteerd met een inactieve zoutoplossing. Omwille van biologische variatie zullen een aantal dieren die geïnjecteerd werden met lage dosissen van de toxische stof, het er vaak beter van af brengen dan sommige controledieren. Hierdoor kunnen geobserveerde effecten zowel toevallig zijn als wijzen op een systematisch effect. Bovendien moeten we ons afvragen of de controlegroep en de met substantie-geïnjecteerde groep een vergelijkbare gezondheid hebben. Zo niet, dan zou een mogelijk verschil in respons ook mede hierdoor verklaard kunnen worden.
Het doel van statistiek is precies om orde te scheppen in de chaos door duidelijk te maken hoeveel variatie op de gegevens toe te schrijven valt aan systematische verschillen (bijvoorbeeld, door het al dan niet inspuiten van een bepaalde substantie) en hoeveel aan toeval of biologische variatie.
Statistiek is immers de wetenschap rond verzamelen, exploreren en analyseren van data. Ze laat toe
- om tot een goede proefopzet te komen,
- om te leren uit data en
- om hierbij variabiliteit en onzekerheid te
- kwantificeren
- controleren
- rapporteren
- d.m.v. statistische besluitvorming modellen op een formele wijze te toetsen aan de data.
Ze vervult daarom een belangrijke rol in zowat alle wetenschappen. Zie ondermeer de populaire column ‘’points of significance’’ in Nature Methods. (http://blogs.nature.com/methagora/2013/08/giving_statistics_the_attention_it_deserves.html)
In deze inleiding situeren we Statistiek in de Wetenschappelijke Methode.
1.1 De Wetenschappelijke Methode
Het doel van wetenschap is het begrijpen van de natuur (van het allerkleinste tot het allergrootste, van vroeger en nu tot in de toekomst). De Wetenschappelijke Methode is de methodiek die vandaag de dag algemeen aanvaard wordt om onze wetenschappelijke kennis van de natuur op te bouwen. Twee belangrijke pijlers van de Wetenschappelijke Methode zijn theorie en observatie. Een wetenschappelijke theorie voorspelt hoe een natuurlijk proces zich gedraagt. Observaties kunnen gebruikt worden om deze theorie te bevestigen of te ontkrachten. Een wetenschappelijke theorie kan dus nooit bewezen worden door observatie, maar kan wel ontkracht worden door observatie. Dit is het falcificatieprincipe van de wetenschapsfilosoof Karl Popper (1902-1994).
De levenswetenschappen berusten op empirisch onderzoek omdat observaties nodig zijn om de kennis uit te breiden. Theorieën kunnen gepostuleerd worden zonder observatie (hoewel dit zelden gebeurt), maar de wetenschapsgemeenschap neemt ze typisch maar voor waar aan nadat de nieuwe theorieën aan observatie getoetst worden.
Figuur 1.1 is een schematische weergave van de Wetenschappelijke Methode.
De natuur staat bovenaan de driehoek. Dit stelt het universum, de wereld, de werkelijkheid of de waarheid voor, waarover de mens kennis wil verzamelen.
Een model (of een theorie) stelt een denkbeeld van een aspect van de natuur voor. Een model laat toe om voorspellingen, verder predicties genoemd te maken over het gedrag van een aspect van de natuur. Hierbij wordt niet noodzakelijk een mathematisch model bedoeld, maar kan het ook een kwalitatieve beschrijving zijn van een aspect van de natuur (bv. insecticide behandeling van planten leidt tot een vermindering van het aantal schadelijke insecten op de planten en tot een verhoogde opbrengst van de oogst).
Via een wetenschappelijk experiment worden data uit de natuur gehaald. Data vormen een manifestatie van het werkelijke gedrag van de natuur. Het experiment moet representatief en reproduceerbaar zijn
Statistische Besluitvorming (Engels: statistical inference) vormt de brug tussen het model van de natuur en de data uit de natuur. Statistische Besluitvorming laat toe op een formele wijze het model te toetsen aan de data en te besluiten in welke mate de wetenschappelijke gemeenschap de theorie en het model voor waar mag aannemen.
- Statistiek wordt ingeroepen omdat de Wetenschappelijke Methode niet zonder doel gebruikt wordt. Wetenschappers hebben gedeeltelijke kennis van de natuur via een aantal modellen/theorieën, maar deze kennis doet nieuwe vragen ontstaan. Dit leidt tot een nieuwe onderzoeksvraag (bijvoorbeeld: zorgt het gebruik van insecticiden voor minder schade van insecten aan de plant?), welke vervolgens verfijnd wordt in een nauwkeurig geformuleerde hypothese (bijvoorbeeld: Het aantal aangetaste bladeren is gelijk voor onbehandelde en pesticide-behandelde planten). Een hypothese is zodanig geformuleerd dat ze door data kan verworpen worden indien de hypothese niet waar zou zijn. De formulering van de hypothese bepaalt mede hoe het experiment moet opgezet worden om de meest informatieve data (evidentie) te kunnen bekomen om vervolgens via de statistische besluitvoering tot een conclusie (i.e. antwoord op de onderzoeksvraag) te komen. Statistiek als wetenschapdiscipline treedt dus op in drie domeinen:
- Proefopzet (“Experimental Design”): het ontwerpen van het exeriment,
- Data-exploratie en beschrijvende statistiek (“Data-exploration and Descriptive Statistics”): het exploreren, samenvatten en visualiseren van de data en
- Statistische besluitvorming (“Statistical Inference”): het veralgemenen van de resultaten in de steekproef naar de populatie toe.
We komen nog even terug of het falcificatieprincipe. Doorheen deze cursus zal het duidelijk worden dat statistiek methoden aanlevert die toelaten om na te gaan in welke mate data consistent zijn met een vooropgestelde model. Indien de data consistent zijn met het model zullen we niet noodzakelijk onmiddellijk besluiten dat de theorie en het model correct zijn. De wijze waarop de data tot stand gekomen zijn via de opzet van experiment speelt hierbij ook een belangrijke rol. Het experiment moet eigenlijk zo opgezet worden dat het model uitgedaagd wordt. Pas als alle moeite gedaan is om te pogen data te bekomen die inconsistent zijn met het model, kunnen de theorie en het model als waar beschouwd worden met een grote waarschijnlijkheid. Wanneer de data inconsistent zijn met het gepostuleerde model, dan kan direct besloten worden dat het model niet juist is.
De Wetenschappelijke Methode heeft een cyclisch karakter: bij het vaststellen van een foutief model zal de wetenschapper het model aanpassen en doorloopt hij opnieuw alle stappen van de Wetenschappelijke Methode.
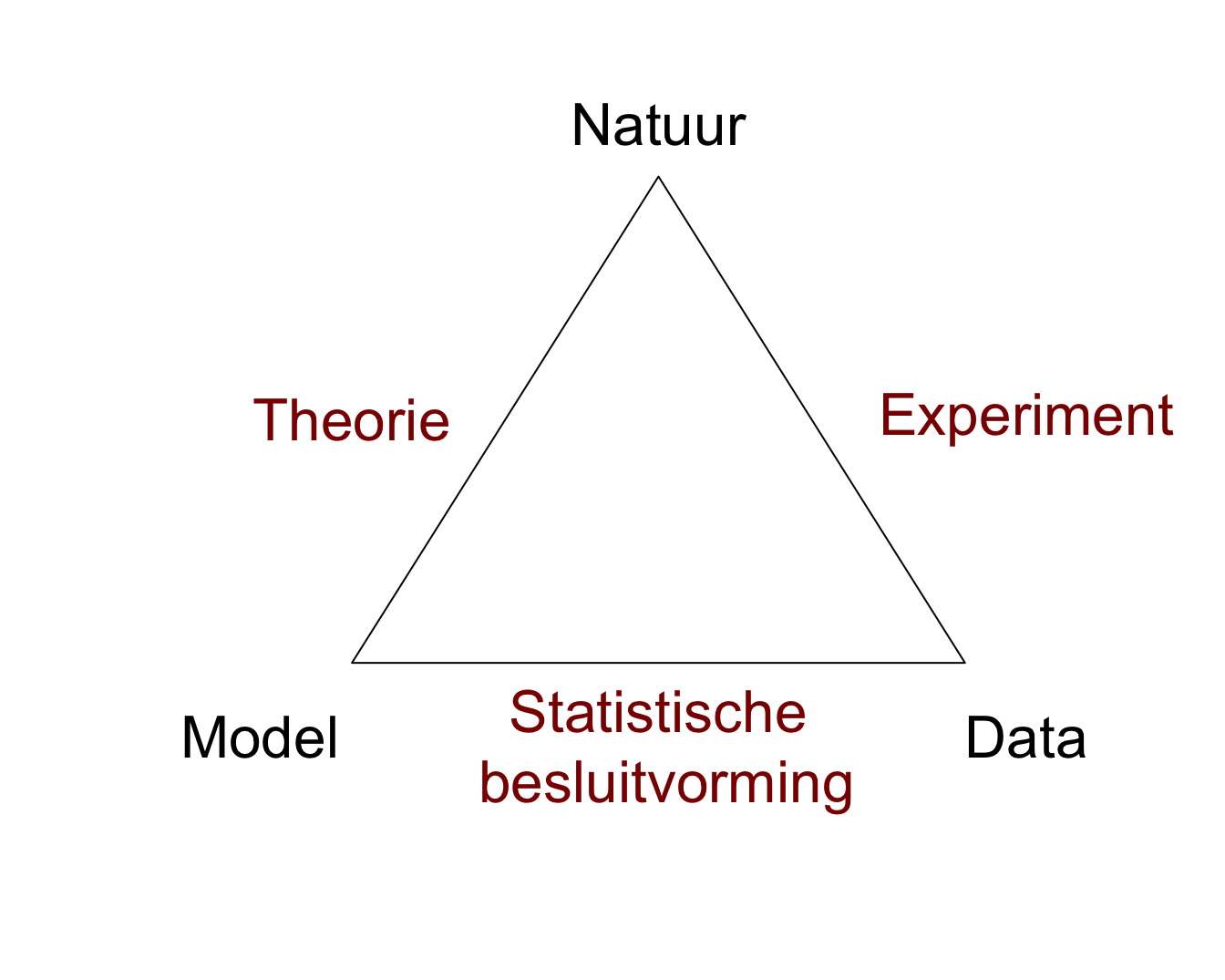
Figuur 1.1: De Wetenschappelijke Methode en de rol van Statistiek.
Een andere belangrijke rol van de Statistiek die verder in deze cursus wordt behandeld, is om de reproduceerbaarheid van wetenschappelijk onderzoek te waarborgen, binnen zelf gekozen probabiliteitsgrenzen (onzekerheid / zekerheid).
1.2 Voorbeeld: Horizon - Homeopathy the test
BBC reportage over homeopathie https://www.dailymotion.com/video/x19idby
1.2.1 Wetenschappelijke hypothese (fragmenten 1-2: 0’00’‘-6’00’‘& 7’40’‘-11’30’’)
Dr. J. Benveniste was een bekende Franse immunoloog die basofiele granulocyten, een soort van witte bloedcellen, bestudeerde. Basofiele granulocyten, ook wel basofielen genoemd, hebben verscheidene Immunoglobuline E (IgE)-receptoren op het membraan die antigenen kunnen binden. Als dit type van granulocyten in contact komen met allergenen dan worden ze geactiveerd en laten hun granules vrij, wat uiteindelijk kan leiden tot een allergische reactie. Benveniste ontwikkelde een test waarbij hij de actieve en inactieve basofielen kon onderscheiden aan de hand van een kleurreactie. Hierdoor kon hij allergische reacties opsporen door het aantal gekleurde basofielen (diegene die de granules vrijgelaten hebben) in een staal te tellen en te vergelijken met een controle staal. Een onderzoeker in zijn labo deed echter eigenaardige bevindingen. Heel hoge verdunningen van anti-IgE antilichamen activeert de degranulatie van humane basofielen, een bevinding die het werkingsmechanisme van homeopathie lijkt te ondersteunen.
Om deze laatste bevinding te testen, pakten Dr. Benveniste en zijn team het onderzoek aan volgens de principes van de wetenschappelijke methode.
- Een nieuwe hypothese werd geponeerd: The Memory of Water.
- Deductie: Als een substantie van anti-IgE antilichamen sterk wordt verdund en heftig wordt geschud, dan wordt de informatie overgedragen naar het water zodat een reactie kan worden gedetecteerd door de allergietest met gemodificeerde basofielen bij extreem grote verdunningen.
- Zet een nieuw experiment op om ``Memory of Water’’-hypothese te evalueren
- Verken, analyseer en interpreteer de resultaten uit het experiment
- Verspreiden van resultaten
Hun werk verscheen in Nature, Davenas et al. (1988), met een “Editorial Reservation: Readers of this article may share the incredulity of the many referees who have commented on several versions of it during the past several months. The essence of the result is that an aqueous solution of an antibody retains its ability to evoke a biological response even when diluted to such an extent that there is a negligible chance of there being a single molecule in any sample. There is no physical basis for such an activity. With the kind collaboration of Professor Benveniste, Nature has therefore arranged for independent investigators to observe repetitions of the experiments. A report of this investigation will appear shortly.”
1.2.2 Onderzoek dient reproduceerbaar te zijn. Wat ging er fout? (Fragment: 14’50”-18’56”)
Een week na publicatie bezocht een team bestaande uit Nature editor Sir John Maddox, een wetenschappelijke fraudebuster Walter W. Stewart en goochelaar en scepticus James Randi, het labo van Benveniste zodat hij zijn resultaten kon reproduceren onder gecontroleerde contities. Tijdens een eerste drie pogingen kon het team van Benveniste de resultaten reproduceren en werd hoge activiteit van de basofielen bevestigd wanneer ze in contact werden gebracht met de extreem sterk verdunde substantie.
Dr. Stewart merkte op dat de onderzoekers die de tellingen verrichten, wisten welke stalen behandeld werden met de controle en welke met de extreem verdunde substantie. En hij stelde een dubbelgeblindeerde proefopzet voor, waarbij geen van de onderzoekers wist welke stalen de controle en welke de behandelde stalen waren. De stalen werden in een aparte geblindeerde kamer voorbereid en gerandomiseerd. De codes werden aan het plafond van het lab geplakt. Onder deze meer rigoureuze procedure kon het team van Benveniste de resultaten niet langer reproduceren.
Wat ging er fout?
- Proefopzet: Bias kan worden geïntroduceerd als de wetenschapper weet hoe de stalen worden behandeld.
Oplossing?
- Blindering (“Blinding”)
- At random codes toe te wijzen aan de stalen
- De codes worden gebroken nadat alle data is gecollecteerd
- Hoe subjectiever de meting hoe belangrijker blindering is
- Dubbele blindering (“Double blinding”): Zowel proefpersoon als wetenschapper weten niet welke behandeling er werd gegeven
- Dubbelgeblindeerde proeven zijn de standaard in geneesmiddelenonderzoek. Het is immers nooit voldoende om enkel een nieuw middel aan een aantal patiënten toe te dienen om de werkzaamheid te evalueren. Er moet steeds een controlegroep zijn die geen werkzaam geneesmiddel krijgt, maar een placebo, zodat de effecten daarvan kunnen worden vergeleken met die van het “effectieve” middel. Men heeft dan ook als doel om te bewijzen dat een stof beter werkt dan het placebo-effect. Cruciaal hierbij is dat de arts die het middel voorschrijft, de arts die het effect beoordeelt noch de patiënt mogen weten wie de effectieve behandeling kreeg en wie het placebo kreeg. Dit om te vermijden dat de artsen hun eigen verwachtingen over het middel onbewust aan de patiënt over zouden dragen, of dat het oordeel van de artsen over de toestand van de patiënt na de behandeling beïnvloed zou worden (vb Fragment: 19’00’’-20’30“).
Dit voorbeeld wijst dus op het belang van een goeie controle!
1.2.3 The ultimate test - proefopzet (Fragment 31’00-39’30’’)
“The Memory of Water” hypothese duikt nog geregeld op in de wetenschappelijke literatuur. Telkens betreft het echter onderzoek met gebrekkige controles of kon het onderzoek niet gereproduceerd worden. James Randy speelt met zijn “one-million-dollar-challenge” in op deze onderzoeken. Als scepticus looft hij een prijs uit voor eenieder die onder gecontroleerde condities claims hard kan maken die volgens de huidige wetenschappelijk kennis onmogelijk zijn.
Het team van Horizon gaat de “one-million-dollar-challenge” aan. Onder goedkeuring van James Randy zetten zij de volgende proef op om de “The Memory of Water” hypothese te onderzoeken. Een stockoplossing van actieve stof en een negatieve controle worden aangemaakt en ondergaan dezelfde stappen. Om mogelijke contaminatie effecten uit te sluiten worden ze beiden verdund. Eerst worden 2 x 5 proefbuizen met verdunning van 5C (5 opeenvolgende verdunningen van 1 op 100) gemaakt: 5 met actieve stof en 5 met puur water. Deze 10 tubes worden random gelabeld. Hier wordt dus wel op een effectieve manier gebruik gemaakt van blinding. Na het labelen volgt een verdere verdunning tot 18C. Vervolgens worden de stalen herlabeld om alle fraude te voorkomen en worden de stalen naar twee onafhankelijke labo’s gestuurd (Marion en Wayne). In het labo voegen de onderzoekers de humane basofiel granulocyten toe. Via flowcytometrie, een objectievere meting dan manuele tellingen, wordt nagegaan hoeveel cellen zijn geactiveerd. De labo’s werd meegedeeld dat er 20 actieve en 20 placebo oplossingen zijn om te voorkomen dat alle stalen als niet actief worden geklasseerd. Hierna geeft elk labo zijn ruwe flowcytometrie metingen, proportie actieve cellen per staal en klassering van de stalen door.
1.2.4 The ultimate test - data analyse (Fragment 39’30-43’00’’)
Nadat alle labo analyses zijn uitgevoerd, verzamelen alle wetenschappers, journalisten en James Randy zich in “the Royal Society”. Een statisticus analyseert de gegevens. Bij het verkennen van de data, ook de data exploratie genoemd, bleken bepaalde stalen meer activiteit te vertonen dan anderen. De vraag is of dit systematisch het geval is voor “sterk-verdunde” stalen.
In het Marion labo werden 9 proefbuizen van extreme verdunning (D) en 11 van de controles (C) negatief gelabeld. Omdat onderzoekers wisten dat er 20 actieve proefbuizen (D) en 20 controle proefbuizen (C) waren, weten we ook dat er 11 (D) en 9 (C) stalen als positief werden gelabeld.
| negatief | postief | totaal | |
|---|---|---|---|
| sterk verdund (D) | 9 | 11 | 20 |
| controle (C) | 11 | 9 | 20 |
| totaal | 20 | 20 | 40 |
| negatief | postief | totaal | |
|---|---|---|---|
| sterk verdund (D) | 10 | 10 | 20 |
| controle (C) | 10 | 10 | 20 |
| totaal | 20 | 20 | 40 |
Enerzijds zou men in het experiment een lichte aanwijzing kunnen zien dat er in de stalen met extreme verdunning activiteit is: 11/20 stalen werden correct geklasseerd. Anderzijds, zou het kunnen dat de 11/20 berust op toeval. Als er geen effect is van D zal men door toeval toch resultaten vinden die lichtjes afwijken van 10/20. Maar hoeveel is “lichtjes”: 11/20? 12/20? 13/20? …
Hoeveel correcte positieve tests \(x\) zijn er nodig om voldoende bewijskracht te hebben voor werking van D? We kunnen dit onderbouwen met kans om ten minste \(x\) correcte positieve tests te vinden door zuiver toeval wanneer D niet verschilt van C. \[p=P(\text{ten minste } x \text{ correcte positieve tests} \vert \text{effect D= effect C})\]
Dergelijke kansen kunnen worden berekend door gebruik te maken van probabiliteitstheorie (Tabel 1.3):
knitr::kable(cbind(x=11:15,
p=phyper(q=10:14,m=20,n=20,k=20,lower.tail=FALSE)), tableType,
caption = 'Kans op tenminste $x$ correct geklasseerde "sterk-verdunde" stalen wanneer er in werkelijkheid geen effect is.',
booktabs = TRUE,digits=4
)| x | p |
|---|---|
| 11 | 0.3762 |
| 12 | 0.1715 |
| 13 | 0.0564 |
| 14 | 0.0128 |
| 15 | 0.0019 |
- Als er geen verschil is tussen C en D, dan zal men in 37.6% van de experimenten door toeval een \(x\) observeren van minstens 11
- Het experiment geeft dus absoluut geen bewijs voor de werking van de verdunning D.
| negatief | postief | totaal | |
|---|---|---|---|
| sterk verdund (D) | 11 | 9 | 20 |
| controle (C) | 9 | 11 | 20 |
| totaal | 20 | 20 | 40 |
Bijgevolg zien we dat we op basis van empirische gegevens nooit met 100% zekerheid conclusies kunnen trekken. De gegevens zijn onderhevig aan random variabiliteit en bijgevolg zijn onze conclusies dat ook.
1.2.5 Mogelijke fouten
- Een experiment is onderhevig aan random variabiliteit bijgevolg zijn de conclusies dat ook.
- Zelfs als D en C equivalent zijn, kan men 15 correcte positieve resultaten observeren door toeval. Dat kunnen we in 2 op de 1000 experimenten verwachten.
- In dergelijke steekproef zal men ten onrechte besluiten dat er bewijs is voor de werking van D terwijl er in realiteit geen verschil is tussen D en C.
- Intuïtief voelen we aan dat we niet met absolute zekerheid uitspraken kunnen doen over populatiekarakteristieken op basis van een eindige steekproef.
In deze cursus zullen we daarom steeds volgende facetten van de statistiek bespreken:
- Proefopzet: hoe zijn de gegevens tot stand gekomen
- Data exploratie en beschrijvende statistiek: exploreren, visualiseren, samenvatten en beschrijven van geobserveerde data zodat relevante aspecten naar voor komen.
- Statistische besluitvorming: aan de hand van statistische modellen bestuderen in hoeverre geobserveerde trends/effecten die geobserveerd worden in een steekproef veralgemeend kunnen worden naar de algemene populatie.
References
Davenas, E., F. Beauvais, J. Amara, M. Oberbaum, B. Robinzon, A. Miadonnai, A. Tedeschi, et al. 1988. “Human Basophil Degranulation Triggered by Very Dilute Antiserum Against Ige.” Nature 333 (6176): 816–18. http://dx.doi.org/10.1038/333816a0.