Hoofdstuk 4 Data exploratie en beschrijvende statistiek

4.1 Inleiding

Om de resultaten van een experimentele of observationele studie te rapporteren, is het uiteraard niet mogelijk om per subject waarvoor gegegevens verzameld werden in de studie de bekomen gegevens neer te schrijven. Met de veelheid aanwezige informatie is het integendeel belangrijk de gegevens gericht samen te vatten en voor te stellen. Zelfs wanneer het duidelijk is welke analyse er moet uitgevoerd worden, moet er eerst een basisbeschrijving komen van de verzamelde gegevens. Dit zal mee helpen aangeven of er geen fouten zijn gemaakt tijdens het onderzoek of bij de registratie van gegevens. Eventuele anomalieën of zelfs fraude worden in deze fase opgespoord en tenslotte krijgt men een indruk of voldaan is aan de onderstellingen (bvb. de onderstelling dat de gegevens Normaal verdeeld zijn¹³) die aan de grond liggen van de voorgestelde statistische analyses in de latere fase.

De eerste vraag die moet gesteld worden bij het benaderen van een echte data set is:

Wat is de oorspronkelijke vraagstelling (geweest), waarom zijn deze gegevens verzameld?
Hoe en onder welke omstandigheden zijn de subjecten gekozen en de variabelen gemeten? Hierbij stelt men meteen de vraag naar het design van de studie, alsook hoeveel subjecten werden aangezocht voor meetwaarden en hoeveel daar uiteindelijk echt van in de database zijn terecht gekomen (m.a.w. of gegevens die men gepland had te verzamelen, om een of andere reden toch niet bekomen werden). Bovendien laat dit toe om te evalueren of verschillende subjecten in de studie al dan niet meer verwant zijn dan andere subjecten en of de analyse hier rekening mee moet houden.
Is er een specifieke numerieke code die een ontbrekend gegeven of ander type uitzondering voorstelt in plaats van een echte meetwaarde?

Als het vertrekpunt duidelijk is en alle variabelen goed beschreven zijn, kan men starten met een betekenisvolle exploratie van de gerealiseerde observaties.

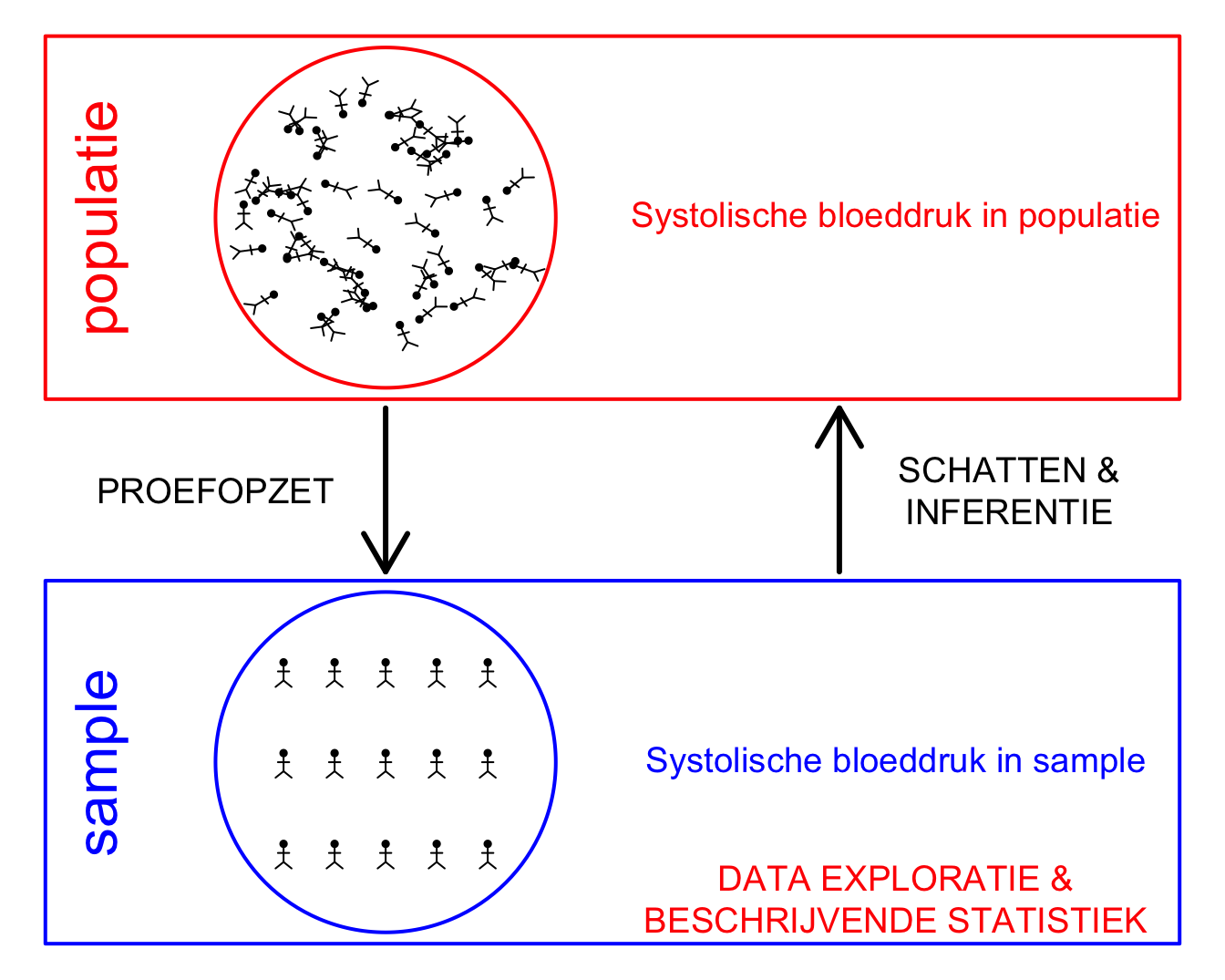
Figuur 4.1: Verschillende stappen in een studie. In dit hoofdstuk ligt de focus op de data-exploratie en beschrijvende statistiek

Dit hoofdstuk zullen werken rond een centrale dataset: de NHANES studie.

Voorbeeld 4.1 (NHANES studie)

De National Health and Nutrition Examination Survey (NHANES) wordt sinds 1960 op regelmatige basis of genomen. In dit voorbeeld maken we gebruik van de gegevens die werden verzameld tussen 2009-2012 bij 10000 Amerikanen en die werden opgenomen in het R-pakket NHANES. Er werd een groot aantal fysische, demografische, nutritionele, levelsstijl en gezondheidskarakteristieken gecollecteerd in deze studie (zie Tabel 4.1). Merk op dat ontbrekende waarnemingen hier gecodeerd worden a.d.h.b. de code NA (Not Available / Missing Value)

**Einde voorbeeld**

Tabel 4.1: Overzicht van een aantal variabelen uit de NHANES studie.
ID	Gender	Age	Race1	Weight	Height	BMI	BPSysAve	TotChol	SmokeNow	Smoke100
51624	male	34	White	87.4	164.7	32.22	113	3.49	No	Yes
51625	male	4	Other	17.0	105.4	15.30	NA	NA	NA	NA
51630	female	49	White	86.7	168.4	30.57	112	6.70	Yes	Yes
51638	male	9	White	29.8	133.1	16.82	86	4.86	NA	NA
51646	male	8	White	35.2	130.6	20.64	107	4.09	NA	NA
51647	female	45	White	75.7	166.7	27.24	118	5.82	NA	No

4.2 Univariate beschrijving van de variabelen

In de regel begint men met een univariate inspectie: elke variabele wordt apart onderzocht. Het is absoluut aan te raden om hierbij eerst alle ruwe gegevens te bekijken door middel van grafieken (zie verder) alvorens naar samenvattingsmaten (zoals het gemiddelde) over te stappen. Dit laat toe om een idee te krijgen hoe de geobserveerde waarden van een veranderlijke verdeeld zijn in de studiegroep (bvb. welke verdeling de bloeddrukmetingen in de studie hebben) en of er eventuele uitschieters (d.i. extreme metingen of outliers) zijn. Met outliers worden observaties aangegeven die ten opzichte van de geobserveerde verdeling van de waarden in de data set, extreem zijn, buitenbeentjes.

#De data van de NHANES studie bevindt zich
#in het R package NHANES
library(NHANES) #laad NHANES package

#NHANES is een data frame met de gegevens
#De rijen bevatten informatie over elk subject
#De kolommen de variabelen die werden geregistreerd
#vb variabele Gender, BMI, ...
#Een variabele (kolom) kan uit de dataframe
#worden gehaald door gebruik van het $ teken
#en de naam van de variabele
# We slaan de frequentietabel voor variable Gender
# op in object 'tab'

tab <- table(NHANES$Gender)
tab

## 
## female   male 
##   5020   4980

barplot(tab) #teken staaf diagram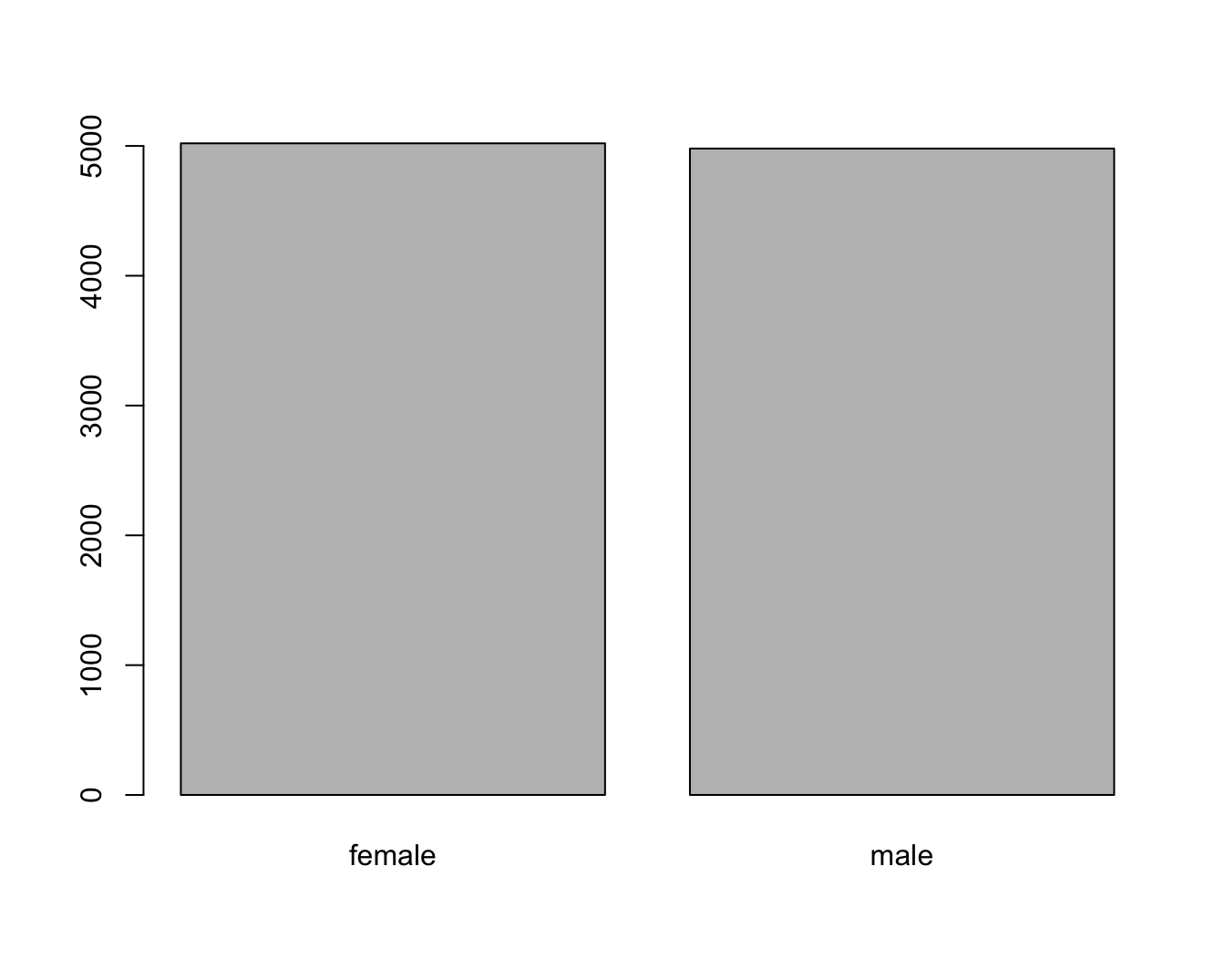

Figuur 4.2: Staafdiagram van het aantal mannen en vrouwen in de NHANES studie.

Er zijn weinig methoden voorhanden om nominale variabelen te beschrijven. In Voorbeeld 4.1 is de variable Gender kwalitatief nominaal. Alles is gezegd over de verdeling van het geslacht als we weergeven hoeveel vrouwen en mannen zijn opgenomen in de studie. Meer nog, als het totale aantal personen in de data set eenmaal vast ligt, dan zijn de uitkomsten verder volledig gekarakteriseerd door, bijvoorbeeld, alleen het percentage vrouwen en mannen weergeen. In het softwarepakket R kan men een beeld van de gegevens krijgen door ze in een frequentietabel weer te geven of a.d.h.v. een grafiek zoals een staafdiagram. Beiden worden gegenereerd in de R-code voor Figuur 4.2. We stellen vast dat 5020 van de 10000 subjecten, ofwel 50.2% vrouwen in de studie zijn opgenomen.

Een staafdiagram geeft op de X-as de mogelijke uitkomsten van de variabele aan (bvb. geslacht). Daarbovenop komt een staaf met hoogte evenredig aan het totaal aantal keer dat die waarde voorkomt in de dataset. In het bijzonder kan men kiezen tussen de absolute frequentie (5020 voor het aantal vrouwen, 4980 voor het aantal mannen) of de relatieve frequentie ( 50.2% vrouwen, 49.8% mannen). De staven staan los van elkaar met een breedte die constant is, maar verder willekeurig. Als de steekproef representatief is voor de populatie, dan krijgen we hier misschien een eerste impressie dat er iets meer vrouwen zijn in de populatie.

De variabele met de naam BMI_WHO in de dataset is kwalitatief ordinaal en heeft 4 geordende categorieën die grensen voor ondergewicht, normaal gewicht, licht-overgewicht, obesitas. Voor dergelijke ordinale variabelen worden de mogelijke uitkomsten best in volgorde gesorteerd en in een frequentietabel of staafdiagram weergegeven. Naast de (relatieve) frequentie is het nu ook zinvol om de cumulatieve (relatieve) frequentie aan te geven. Deze laatste drukt uit welk percentage van de gegevens in de gegeven klasse of een lagere klasse valt. In Figuur 4.3 vind je het staafdiagram voor het BMI. In de R-code voor de figuur vind je tevens de bijhorende frequentietabel.

# sla freq. tabel op in object 'tabBmi'
tabBmi <- table(NHANES$BMI_WHO)
tabBmi

## 
##    12.0_18.5 18.5_to_24.9 25.0_to_29.9    30.0_plus 
##         1277         2911         2664         2751

#teken staaf diagram
barplot(tabBmi)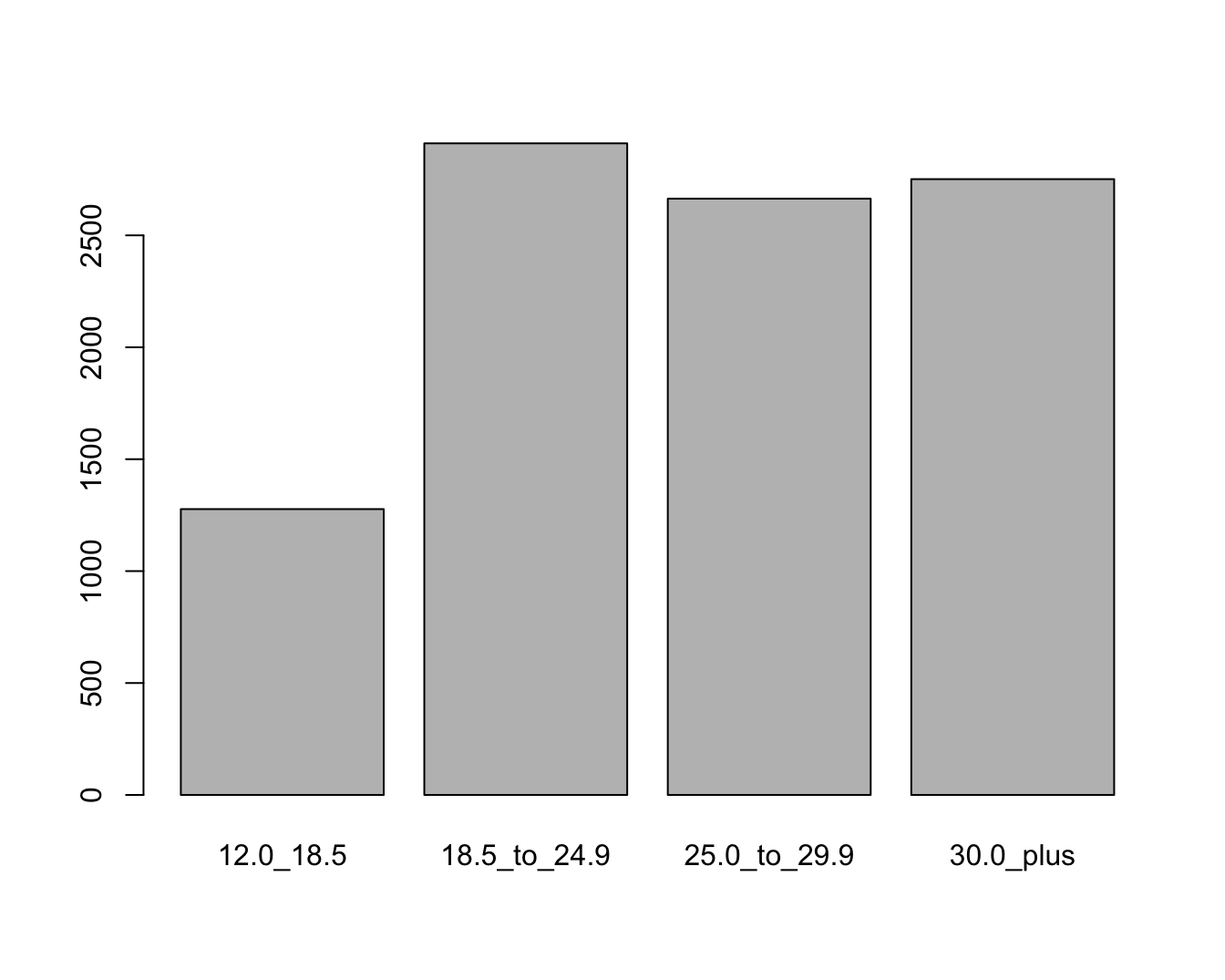

Figuur 4.3: Staafdiagram van het aantal personen in de NHANES studie die behoort tot elke BMI klasse.

Voor numerieke continue variabelen wordt het moeilijk om de frequentie van alle uitkomstwaarden in een tabel te klasseren omdat veel waarden hoogstens 1 keer voorkomen. Het tak-en-blad diagram (in het Engels: stem and leaf plot is een middel om toch nog alle uitkomsten weer te geven. Een voorbeeld is weergegeven in onderstaande R-output voor het BMI in de NHANES studie.

stem(NHANES$BMI)

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   1 | 33333333333333333344444444444444444444444444444444444444444444444444+37
##   1 | 55555555555555555555555555555555555555555555555555555555555555555555+1389
##   2 | 00000000000000000000000000000000000000000000000000000000000000000000+2264
##   2 | 55555555555555555555555555555555555555555555555555555555555555555555+2610
##   3 | 00000000000000000000000000000000000000000000000000000000000000000000+1693
##   3 | 55555555555555555555555555555555555555555555555555555555555555555555+635
##   4 | 00000000000000000000000000000000000000000000000000000000000000000000+255
##   4 | 55555555555555555555555556666666666666666666666666666666666777777777+46
##   5 | 0000011111122222233333444444444444
##   5 | 5556677777789999
##   6 | 133444
##   6 | 567899
##   7 | 
##   7 | 
##   8 | 111

Hier wordt van alle uitkomsten het eerste cijfer of de eerste paar cijfers op een verticale lijn in volgorde uitgezet in de vorm van een boomstam. Daaraan worden horizontaal de bladeren gehecht, met name de laatste cijfers van de geobserveerde uitkomsten. De output geeft bijvoorbeeld aan dat er 3 personen zijn waarvan het afgeronde BMI 55 bedraagt, 2 personen met een afgerond BMI van 56, …. Gezien de studie zo groot is, is het tak-en-blad diagram niet erg praktisch voor dit voorbeeld.

In een tak-en-blad diagram krijgt men alle individuele uitkomsten nagenoeg exact te zien, terwijl de vorm die het diagram aanneemt reeds een idee van de verdeling geeft zoals in een histogram (zie verder). Een vuistregel om de vorm van de verdeling het best te zien is het aantal takken ongeveer gelijk te maken aan \(1 + \sqrt{n}\), waarbij \(n\) het aantal observaties voorstelt. Dit aantal kan uiteraard aangepast worden aan de omstandigheden. Een populair alternatief voor het tak en blad diagram is de eenvoudige frequentietabel. Deze kan men bekomen door de continue variabele (bvb. BMI) om te zetten in een kwalitatieve ordinale variabele, waarvoor vervolgens een frequentietabel wordt weergegeven. Merk op dat dit voor het BMI eerst is gebeurd (Figuur 4.3).

Het grafisch equivalent van dergelijke frequentietabel noemt een histogram, hetgeen men in R bekomt via

hist(NHANES$BMI,main="",xlab="BMI") #main is hoofdtitel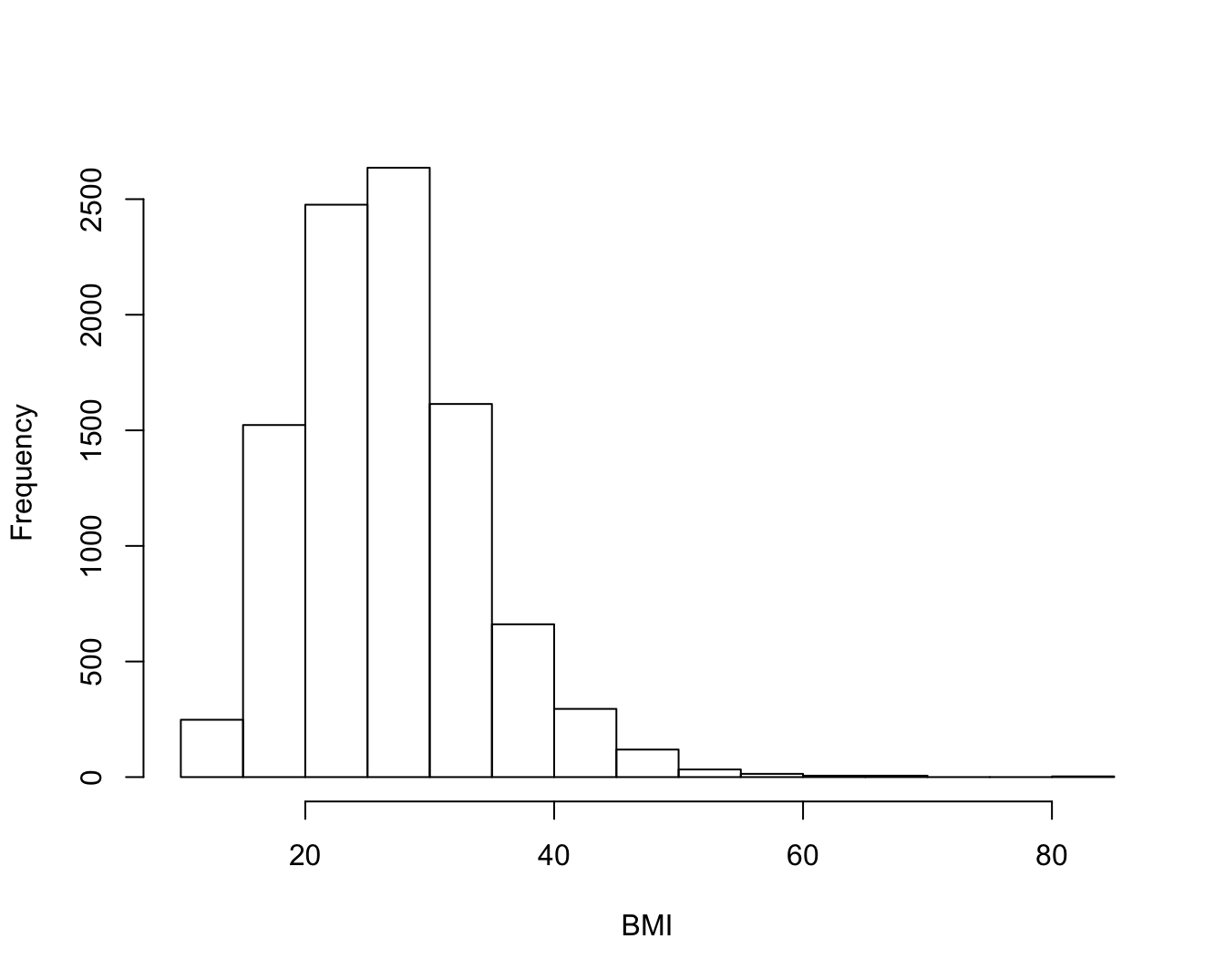

Figuur 4.4: Histogram van het BMI in de NHANES studie.

Wanneer alle klassen een zelfde breedte hebben, worden de absolute of relatieve frequenties per klasse weergegeven door de hoogte van de bijhorende kolom. Bij ongelijke klassebreedtes is het de oppervlakte van de kolom die met de bijhorende klassefrequentie correspondeert. Omdat een histogram met ongelijke klassebreedtes moeilijker te interpreteren is, zijn histogrammen met gelijke klassebreedtes vaak te verkiezen. Als histogrammen voor verschillende groepen bekeken worden, vergemakkelijkt het gebruik van relatieve frequenties i.p.v. absolute frequenties de visuele vergelijkbaarheid.

Op het histogram in Figuur 4.4 worden absolute frequenties weergegeven en klassen met een breedte van 5 eenheden. We stellen vast dat ongeveer 1500 personen van de 10000, of 15% een BMI heeft tussen de 15 en 20.

De keuze van het aantal klassen is van belang bij een histogram. Als er te weinig klassen zijn, dan gaat veel informatie verloren. Als er teveel zijn, dan wordt het algemene patroon verdoezeld door een grote hoeveelheid overbodige details. Gewoonlijk kiest men tussen 5 en 15 intervallen, maar de specifieke keuze hangt af van het beeld van het histogram dat men te zien krijgt.

Indien een voldoende aantal gegevens beschikbaar is, dan kan men een gladdere indruk van de verdeling van de gegevens bekomen door een zogenaamde kernel density schatter te bepalen. Zo’n schatter is een positieve functie die genormaliseerd is in die zin dat de oppervlakte onder de functie 1 is. Ze kan zo geïnterpreteerd worden dat de oppervlakte onder de functie tussen 2 punten \(a\) en \(b\) op de X-as, de kans voorstelt dat een lukrake meting in het interval \([a,b]\) gevonden wordt. Figuur 4.5 toont een histogram (links) en kernel density schatter (rechts) van de het BMI.

# deel grafische scherm op in 1 rij en 2 kolommen
par(mfrow=c(1,2))
# teken een histogram
hist(NHANES$BMI,main="",xlab="BMI")
# teken een kernel density schatter
plot(density(NHANES$BMI,na.rm=TRUE),main="",xlab="BMI")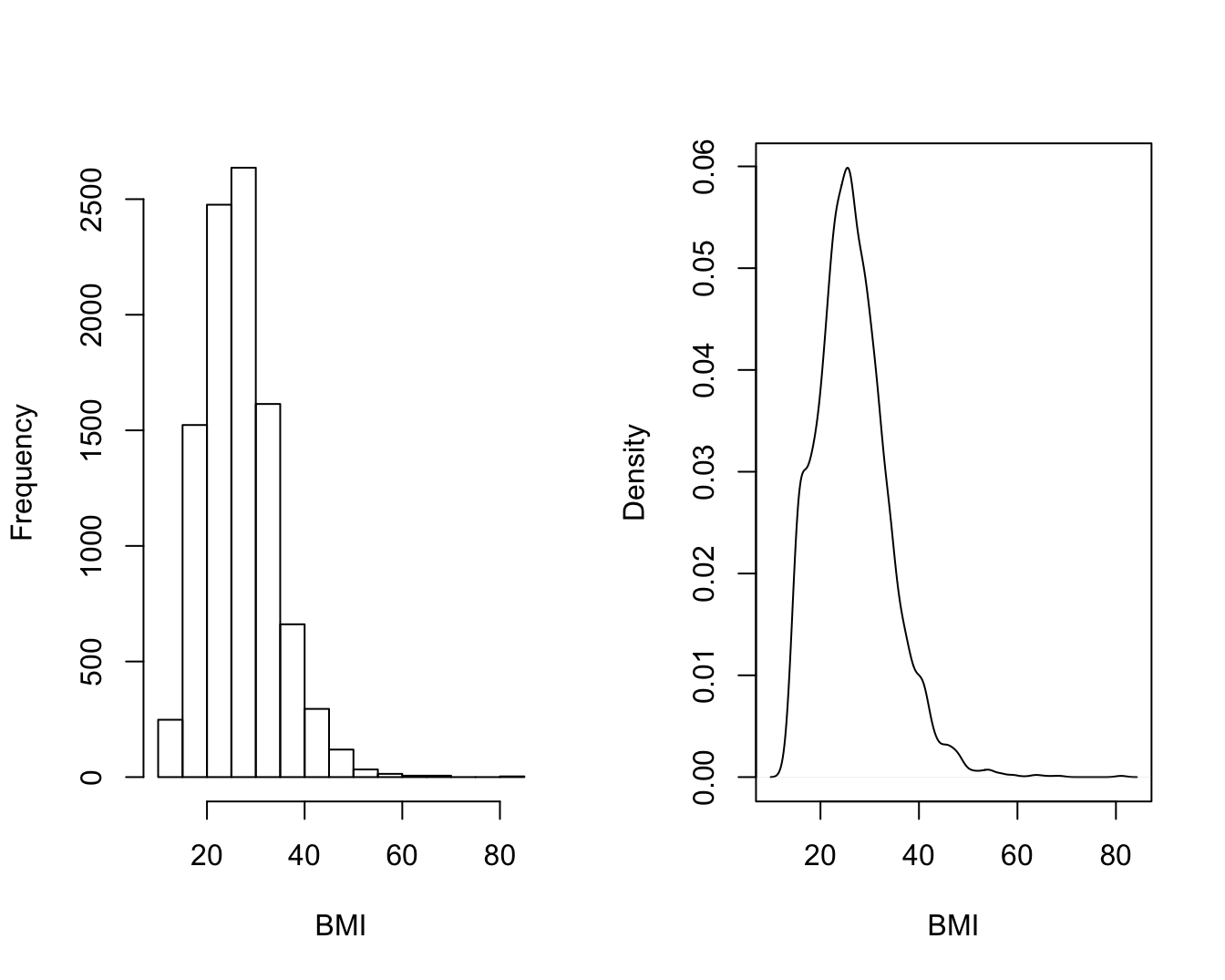

Figuur 4.5: Histogram en kernel density schatter van BMI in de NHANES studie.

# argument na.rm=TRUE omdat er ontbrekende
# waarnemingen (NA) voorkomen

De verdeling kan ook geëvalueerd worden aan de hand van een box-and-whisker-plot, kortweg boxplot genoemd. Deze is meer compact dan een histogram en laat om die reden gemakkelijker vergelijkingen tussen verschillende groepen toe (zie verder). Een Boxplot voor het BMI wordt getoond in Figuur 4.6. De boxplot toont een doos lopend van het 25% tot 75% percentiel met een lijntje ter hoogte van de mediaan (het 50% percentiel) en verder 2 snorharen. Die laatste kunnen in principe lopen tot het minimum en maximum, of tot het 2.5% en 97.5 % of 5% en 95% percentiel. R kiest voor de kleinste en de grootste geobserveerde waarde die geen outlier of extreme waarde zijn. Een meting wordt hierbij een outlier genoemd wanneer ze meer dan 1.5 keer de boxlengte beneden het eerste of boven het derde kwartiel ligt. Een meting wordt een extreme waarde genoemd wanneer ze meer dan 3 keer de boxlengte beneden het eerste of boven het derde kwartiel ligt.

Definitie 4.1 (percentiel) Het 25% percentiel of 25% kwantiel \(x_{25}\) van een reeks waarnemingen wordt gedefinieerd als een uitkomstwaarde \(x_{25}\) zodat minstens \(25\%\) van die waarnemingen kleiner of gelijk zijn aan \(x_{25}\) en minstens \(75\%\) van die waarnemingen groter of gelijk zijn aan \(x_{25}\). Het 75% percentiel of 75% kwantiel van een reeks waarnemingen definieert men als een uitkomstwaarde \(x_{75}\) zodat minstens 75% kleiner of gelijk zijn aan \(x_{75}\) en minstens \(25\%\) van die waarnemingen groter of gelijk zijn aan \(x_{75}\). Algemeen wordt het \(k\%\) percentiel van een reeks waarnemingen gedefinieerd als een waarde (van \(x\)) waarvoor de cumulatieve frequentie gelijk is aan \(k/100.\) Als er meerdere observaties aan voldoen neemt men vaak het gemiddelde van die waarden.

Einde definitie

In R kunnen die als volgt worden bekomen

quantile(NHANES$BMI,c(0.25,.5,.75),na.rm=TRUE)

##   25%   50%   75% 
## 21.58 25.98 30.89

#code om boxplot te genereren
boxplot(NHANES$BMI,ylab="BMI")

#Code om text toe te voegen aan plot
#Dit hoef je zelf normaal gezien niet te doen
BMI=na.exclude(NHANES$BMI)
rangeCl<-quantile(BMI,c(.25,.75))+c(-1,1)*diff(quantile(BMI,c(.25,.75)))*1.5
boxYs<-c(range(BMI[BMI<=rangeCl[2]&BMI>=rangeCl[1]]),quantile(BMI,c(.25,.5,.75)),rangeCl[2]+(max(BMI)-rangeCl[2])/2)

text(1.3,boxYs,labels=c("wisker","wisker","x25","mediaan","x75","outliers"),pos=4,cex=1.3)
lines(c(1.1,1.3,1.3,1.1),c(rangeCl[2],rangeCl[2]+(max(BMI)-rangeCl[2])/2,rangeCl[2]+(max(BMI)-rangeCl[2])/2,max(BMI)),lty=2)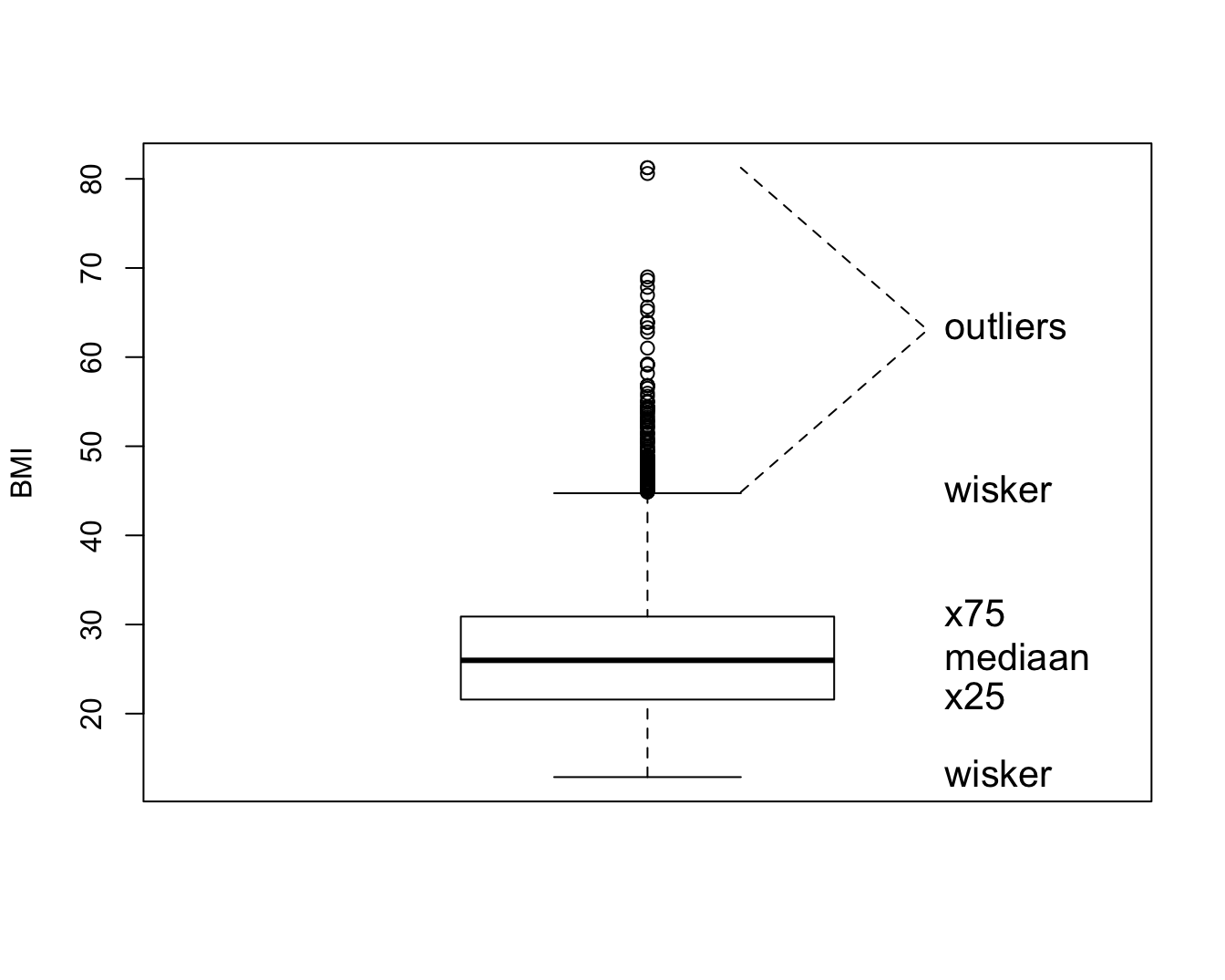

Figuur 4.6: Boxplot van BMI in de NHANES studie.

Bij de inspectie van een dataset speelt het detecteren van outliers in het algemeen een belangrijke rol. Ze kunnen wijzen op fouten, zoals tikfouten of andere fouten die gecheckt en gecorrigeerd moeten worden. Als het geen foutief genoteerde waarden zijn, dan kan het soms wijzen op een subject dat niet echt in de studiepopulatie thuis hoort. Als het in alle opzichten om een bona fide waarde gaat, dan nog is het belangrijk om outliers te detecteren: ze kunnen zeer invloedrijk zijn op de schatting van statistische parameters (zie Sectie 4.3). Als de conclusies van een studie anders liggen met of zonder inclusie van de outlier, dan is dit een ongewenst fenomeen. Men wil immers nooit dat 1 observatie beslissend is voor de conclusies. Dit soort onzekerheid ondermijnt de geloofwaardigheid van de onderzoeksresultaten en vraagt om verdere studie. Binnen de statistiek bestaat een grote waaier aan technieken, zogenaamde robuuste statistische technieken, die erop gericht zijn om de invloed van outliers te minimaliseren. In deze cursus gaan we hier slechts in zeer beperkte mate op in (zie Sectie 4.3, mediaan).

4.3 Samenvattingsmaten voor continue variabelen

Een histogram levert reeds een sterke samenvatting van de geobserveerde, continue gegevens, maar in wetenschappelijke rapporten is er zelden plaats om per geobserveerde variabele dergelijke grafiek voor te stellen. Om die reden is vaak een veel drastischere samenvattingsmaat noodzakelijk. In deze sectie geven we aan hoe de centrale locatie van de gegevens kan beschreven worden, alsook de spreiding van die gegevens rond hun centrale locatie.

4.3.1 Maten voor de centrale ligging

Definitie 4.2 (rekenkundig gemiddelde) Het (rekenkundig) gemiddelde \(\overline{x}\) (spreek uit: x-streep of x-bar) van een reeks waarnemingen \(x_i, i=1, 2, \dots, n\) is per definitie de som van de observaties gedeeld door hun aantal \(n\): \[\begin{equation*} \overline{x}= \frac{x_1 + x_2 + \dots + x_n}{n} =\frac{1}{n} \sum_{i=1}^n x_i \end{equation*}\]

Einde definitie

Een groot voordeel van het gemiddelde als een maat voor de centrale locatie van de observaties is dat het alle data-waarden efficiënt gebruikt vanuit statistisch perspectief. Dit wil zeggen dat ze (onder bepaalde statistische modellen) het maximum aan informatie uit de gegevens haalt en om die reden relatief gezien zeer stabiel blijft wanneer ze herberekend wordt op basis van een nieuwe, even grote steekproef die onder identieke omstandigheden werd bekomen. Bovendien beschrijft het gemiddelde ook verschillende belangrijke modellen voor de verdeling van de gegevens, zoals de Normale verdeling (zie Sectie 4.4). Een groot nadeel van het gemiddelde is dat het zeer gevoelig is aan de aanwezigheid van outliers in de dataset. Om die reden is het vooral een interessante maat van locatie wanneer de verdeling van de observaties (zoals weergegeven door bijvoorbeeld een histogram) min of meer symmetrisch is.

mean(NHANES$BMI,na.rm=TRUE)

## [1] 26.66014

#opnieuw is de na.rm statement hier nodig
#omdat ontbrekende waarden voorkomen.

Indien men de grootste observatie (81.25) vervangt door 8125 om als het ware ene tikfout voor te stellen, dan wijzigt het rekenkundig gemiddelde naar 27.5 en dat terwijl er bijna 10000 BMI metingen zijn. Merk op dat het gemiddelde vrij sterk beïnvloed kan worden door één outlier.

Eigenschap

Als alle uitkomsten \(x_i\) met een willekeurige constante \(a\) worden vermenigvuldigd, dan ook het gemiddelde van die reeks uitkomsten. Als bij alle uitkomsten een constante \(a\) wordt opgeteld, dan ook bij het gemiddelde van die reeks uitkomsten. Formeel betekent dit: \[\begin{eqnarray*} \overline{ax} &= &a \overline{x} \\ \overline{a + x} &= &a + \overline{x} \end{eqnarray*}\] Voor 2 reeksen getallen \(x_i\) en \(y_i\), \(i=1,...,n\), geldt dat het gemiddelde van de som van de observaties gelijk is aan de som van hun gemiddelden: \[\begin{equation*} \overline{x + y} = \overline{x} + \overline{y}. \end{equation*}\] Als de gegevens \(x_i\) enkel de waarden 0 of 1 aannemen, dan is \(\overline{x}\) de proportie subjecten voor wie de waarde 1 werd geobserveerd. Immers, zij \(n_1\) het aantal subjecten binnen de groep van \(n\) subjecten waarvoor de waarde 1 werd geobserveerd, dan is \[\begin{equation*} \overline{x}= \sum_{i=1}^n \frac{x_i}{n} = \frac{n_1}{n}. \end{equation*}\]

Bijvoorbeeld, als we de variabele Gender zó coderen dat mannen een waarde 0 aannemen en vrouwen een waarde 1, dan is het gemiddelde van de variabele Gender gelijk aan 50.2%, hetgeen de proportie is van het aantal vrouwen in de studie. Een percentage kan dus steeds opgevat worden als het gemiddelde van een geschikte variabele.

Einde eigenschap

Een centrale maat die robuuster reageert dan het gemiddelde, d.w.z. minder of niet gevoelig is aan outliers, is de mediaan of het 50% percentiel.

Definitie 4.3 (mediaan) De mediaan, het 50% percentiel of het 50% kwantiel \(x_{50}\) van een reeks waarnemingen \(x_i, i=1, 2, \dots, n\) is per definitie een uitkomstwaarde \(x_{50}\) zodat minstens \(50\%\) van die waarnemingen groter of gelijk zijn aan \(x_{50}\) en minstens \(50\%\) van die waarnemingen kleiner of gelijk zijn aan \(x_{50}\).

Einde definitie

Om de mediaan te schatten, rangschikt men eerst de gegevens volgens grootte. Als het aantal observaties \(n\) oneven is, dan is een schatting voor de mediaan de middelste waarneming. Indien \(n\) even is, dan zijn er 2 middelste waarnemingen en schat men de mediaan (meestal) als hun gemiddelde. Een voordeel van de mediaan is dat ze niet gevoelig is aan outliers. In het bijzonder kan ze vaak nuttig aangewend worden wanneer sommige gegevens gecensureerd zijn. Dit wil zeggen dat men voor een aantal gegevens enkel weet dat ze boven of onder een bepaalde drempelwaarde liggen.

median(NHANES$BMI,na.rm=TRUE)

## [1] 25.98

#Merk op dat we hier gebruik maken van het argument na.rm=TRUE
#Dit komt omdat we niet beschikken over het BMI
#voor elke persoon: ontbrekende waarnemingen
#Die worden in R als een NA voorgesteld
#Als we het argument na.rm=TRUE gebruiken wordt
#de mediaan berekend op basis van de beschikbare observaties

Indien men de grootste observatie (81.25) vervangt 8125, dan wijzigt de mediaan niet. Merk ook op dat de mediaan lager is dan het gemiddelde, hij is minder gevoelig voor de outliers in de dataset.

Definitie 4.4 (modus) De modus van een reeks observaties is de waarde die het meest frequent is, of wanneer de gegevens gegroepeerd worden, de klasse met de hoogste frequentie.

Einde definitie

De modus wordt niet vaak gebruikt in statistische analyse omdat haar waarde sterk afhangt van de nauwkeurigheid waarmee de gegevens werden gemeten. Zo is de modus van de reeks observaties \(1, 1, 1, 1.5, 1.75, 1.9, 2, 2.1, 2.4\) gelijk aan 1, maar wordt ze 2 wanneer alle observaties afgerond worden tot gehele getallen. Bovendien is de modus niet eenvoudig te schatten voor continue data waar de frequentie van elke geobserveerde waarde meestal 1 is. De modus is daarom het meest zinvol voor kwalitatieve en discrete numerieke gegevens, waar ze de meest frequente klasse aanduidt.

Als de observaties uit een symmetrische verdeling afkomstig zijn, vallen de mediaan en het gemiddelde nagenoeg samen (als de geobserveerde verdeling perfect symmetrisch is, vallen ze theoretisch exact samen). De beste schatter voor het centrum van de verdeling op basis van de beschikbare steekproef is dan het gemiddelde eerder dan de mediaan van die observaties. Inderdaad, als men telkens opnieuw een lukrake steekproef neemt uit de gegeven studiepopulatie en voor elke steekproef het gemiddelde en de mediaan berekent, dan zal het gemiddelde minder variëren van steekproef tot steekproef dan de mediaan. Ze is bijgevolg stabieler en wordt daarom een meer precieze schatter genoemd. Intuïtief kan men begrijpen dat het gemiddelde meer informatie uit de gegevens gebruikt: niet alleen of iets groter of kleiner is dan \(x_{50}\) maar ook hoeveel groter of kleiner de exacte waarde van elke observatie is, wordt in de berekening betrokken.

Definitie 4.5 (scheve verdeling) Een niet-symmetrische verdeling wordt scheef genoemd. Als de waarden rechts van de mediaan verder uitlopen dan links, dan is de verdeling scheef naar rechts (in het Engels: positively skew) en is het gemiddelde (meestal) groter dan de mediaan. Als de waarden links van de mediaan verder uitlopen dan rechts, dan is de verdeling scheef naar links (in het Engels: negatively skew) en is het gemiddelde (meestal) kleiner dan de mediaan.

Einde definitie

Voor een niet-symmetrische verdeling is de mediaan veelal een beter interpreteerbare maat dan het gemiddelde omdat ze minder beïnvloed is door de staarten van de verdeling en daarom beter het centrum van de verdeling aanduidt. Maar in sommige gevallen, zoals bijvoorbeeld voor `de gemiddelde opbrengst per week’, blijft het gemiddelde zinvol omdat het meteen verwijst naar de totale opbrengst over alle weken (gelijk aan \(n\) keer het gemiddelde als \(n\) weken werden geobserveerd). Ook voor kwalitatieve variabelen kan een gemiddelde zinvol zijn. Voor binaire nominale variabelen die als 1 of 0 gecodeerd zijn, geeft het gemiddelde immers het percentage observaties gelijk aan 1 weer. Voor ordinale variabelen die bijvoorbeeld gecodeerd zijn als \(1, 2, 3, ...\) levert het gemiddelde soms nuttigere informatie dan de mediaan. Niettemin berust het dan op de impliciete onderstelling dat een wijziging van score van 1 naar 2 even belangrijk is als een wijziging van 2 naar 3.

Om scheve verdelingen in een paar woorden te beschrijven is het vaak nuttig om

ofwel de gegevens te beschrijven in termen van percentielen,
ofwel de gegevens te transformeren naar een andere schaal (bvb. door logaritmen te nemen), zodat ze op de nieuwe schaal bij benadering symmetrisch verdeeld zijn.

Wanneer het gemiddelde groter is dan de mediaan en alle metingen positief zijn (vb concentraties, BMI), dan is een logaritmische transformatie van de gegevens vaak nuttig om de scheefheid weg te nemen. In dit geval is vooral het geometrisch gemiddelde interessant.

Definitie 4.6 (geometrisch gemiddelde) Het geometrische gemiddelde van een reeks waarnemingen \(x_i, i=1, 2, \dots, n\) ontstaat door er de natuurlijke logaritme van te berekenen, het gemiddelde hiervan te nemen en dit vervolgens terug te transformeren naar de originele schaal door er de exponentiële functie van te nemen: \[\begin{equation*} \exp\left\{\frac{1}{n} \sum_{i=1}^n \log(x_i)\right\} \end{equation*}\]

Einde definitie

par(mfrow=c(1,2))
hist(NHANES$BMI, main="histogram van BMI",xlab="BMI")
hist(log(NHANES$BMI), main="histogram van log(BMI)",xlab="log(BMI)")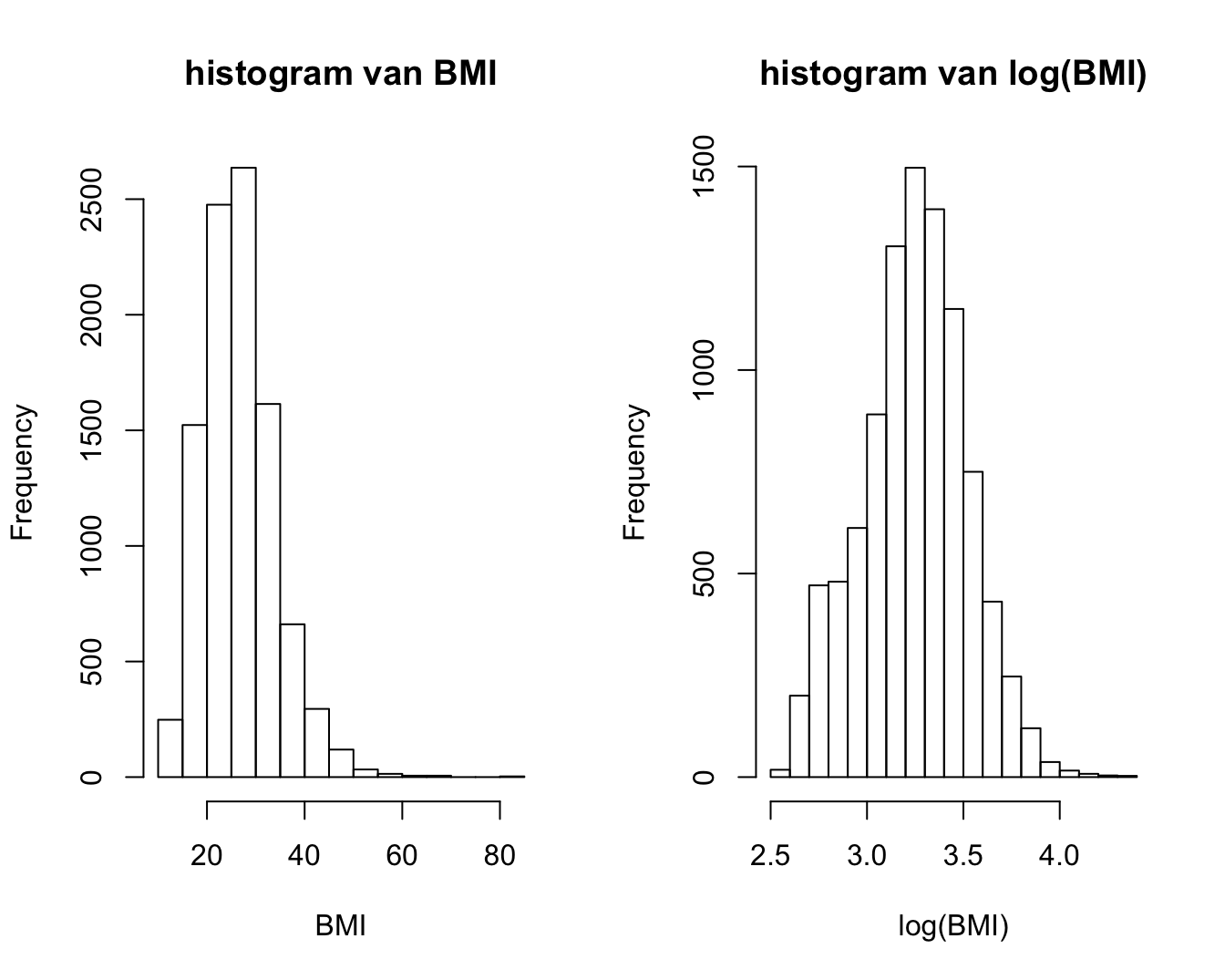

Figuur 4.7: Boxplot van BMI en log(BMI) in de NHANES studie.

In situaties waar de log-transformatie inderdaad de scheefheid wegneemt, zal het geometrisch gemiddelde dichter bij de mediaan liggen dan het gemiddelde. Wanneer de verdeling scheef is, is ze soms zelfs een nuttigere maat voor centrale locatie dan de mediaan:

omdat ze ook gebruik maakt van de exacte waarden van de observaties en daarom doorgaans preciezer is dan de mediaan;
omdat ze, op een transformatie na, berekend wordt als een rekenkundig gemiddelde (weliswaar van de logaritmisch getransformeerde observaties) en algemene statistische technieken voor een gemiddelde (zoals betrouwbaarheidsintervallen (zie volgende hoofdstukken) en toetsen van hypothesen (zie volgende hoofdstukken) daardoor vrijwel rechtstreeks toepasbaar zijn voor geometrische gemiddelden.

Voorbeeld 4.2 (BMI)

Het gemiddelde en mediane BMI bedraagt 26.66 en 25.98 , respectievelijk. Het gemiddelde is hier groter dan de mediaan omdat de BMI scheef verdeeld is naar rechts (zie Figuur 4.7). De verdeling wordt meer symmetrisch na log-transformatie. Het gemiddelde en mediane log-BMI liggen ook dichter bij elkaar en bedragen respectievelijk 3.25 en 3.26. De geometrisch gemiddelde BMI-concentratie bekomen we door de exponentiële functie te evalueren in 3.25, hetgeen ons 25.69 oplevert. Merk op dat dit inderdaad beter met de mediaan overeenstemt dan het rekenkundig gemiddelde.

**Einde voorbeeld**

Tot slot, vooraleer een eenvoudige maat voor de centrale ligging (en spreiding) te construeren of interpreteren, is het goed om altijd eerst de volledige verdeling te bekijken! Immers, stel dat men het gemiddelde of mediaan berekent van gegevens uit een bimodale verdeling (d.i. een verdeling met 2 modi, voor bvb. zieken en niet-zieke dieren). Dan kan het gemiddelde of mediaan makkelijk een zeer zeldzame waarde aannemen die geenszins in de buurt van 1 van beide maxima ligt.

4.3.2 Spreidingsmaten

Nadat de centrale ligging van de gegevens werd bepaald, is men in tweede instantie geïnteresseerd in de spreiding van de gegevens rond die centrale waarde. Er zijn verschillende redenen waarom daar interesse in bestaat:

Om risico’s te berekenen (zie Sectie 4.4) volstaat het niet om de centrale locatie van de gegevens te kennen, maar moet men bovendien weten hoeveel de gegevens rond die waarde variëren. Inderdaad, stel dat men wenst te weten welk percentage van de subjecten een BMI heeft van boven de 35. Wetende dat een geometrisch gemiddelde van 25.69 wordt geobserveerd, zal dat percentage relatief hoog zijn wanneer de metingen zeer gespreid zijn en relatief laag anders.
Veldbiologen zijn vaak geïnteresseerd in de mate waarin dieren of planten verspreid zijn over een zeker studiegebied. Op die manier kunnen ze immers leren over de relaties tussen individuen onderling en met hun omgeving. Daartoe zal men in de praktijk op verschillende plaatsen in het studiegebied tellingen maken van het aantal individuen op die plaats. Men kan aantonen dat, onder bepaalde veronderstellingen, individuen lukraak verspreid zijn over het studiegebied wanneer de spreiding op die tellingen, zoals gemeten door de variantie (zie verder), van dezelfde grootte-orde is als de gemiddelde telling. Indien de spreiding groter is, dan hebben individuen de neiging om zich te groeperen. Andersom, indien de spreiding op die tellingen lager is dan de gemiddelde telling, dan zijn de individuen zeer uniform verdeeld over het studiegebied.
Stel dat men een zekere uitkomst (bvb. het aantal species ongewervelde dieren in een stuk bodemkorst) wenst te vergelijken tussen 2 groepen (bvb. gebieden met en zonder bosbrand), dan zal men een duidelijk beeld van het groepseffect krijgen wanneer de uitkomst weinig gespreid is, maar een veel minder duidelijk beeld wanneer de gegevens meer chaotisch (en dus meer gespreid) zijn. Om uit te maken of een interventie-effect toevallig of systematisch is, moet men daarom een idee hebben van de spreiding op de gegevens.

Dat uitkomsten variëren tussen individuen en binnen individuen omwille van allerlei redenen ligt aan de basis van de statistische analyse van veel fenomenen. Het goed beschrijven van variatie naast de centrale locatie van de gegevens is daarom belangrijk! Hierbij zal men typisch een onderscheid maken tussen variatie die men kan verklaren (door middel van karakteristieken, zoals bijvoorbeeld de leeftijd, van de bestudeerde individuen) en onverklaarde variatie. We gaan dieper in op dit onderscheid in Hoofdstuk 6 rond lineaire regressie.

Variatie betekent dat niet alle observaties \(x_i\) gelijk zijn aan het gemiddelde \(\overline{x}\). De afwijking \(x_i - \bar{x}\) is om die reden interessant. Het gemiddelde van die afwijkingen is echter altijd 0 (verifieer!) omdat positieve en negatieve afwijkingen mekaar opheffen. Bijgevolg levert de gemiddelde afwijking geen goede maat op voor de variatie en is het beter om bijvoorbeeld naar kwadratische afwijkingen \((x_i - \bar{x})^2\) te kijken. Het gemiddelde van die kwadratische afwijkingen rond het gemiddelde, het gemiddelde dus van \((x_i - \bar{x})^2\), levert daarom wel een goede maat op. Merk op dat we bij het berekenen van het gemiddelde niet delen door het aantal observaties \(n\), maar door \(n-1\) waarbij we corrigeren voor het feit dat we voor de berekening van de steekproef variantie 1 vrijheidsgraad hebben gespendeerd aan het schatten van het gemiddelde.

Definitie 4.7 (variantie) De variantie een reeks waarnemingen \(x_i, i=1, 2, \dots, n\) is per definitie \[\begin{equation*} s^2_x = \sum_{i=1}^{n} \frac{(x_i - \bar{x})^2}{n-1} \end{equation*}\]

Als duidelijk is om welke waarnemingen het gaat, wordt dit ook met \(s^2\) genoteerd.

Einde definitie

Indien alle observaties gelijk waren en er dus geen variatie was, dan zou hun variantie 0 bedragen. Hoe meer de gegevens uitgesmeerd zijn rond hun gemiddelde, hoe groter \(s^2\). Helaas is de waarde van de variantie zelf niet gemakkelijk te interpreteren. Dit is deels omdat door het kwadrateren de variantie niet langer de dimensie van de oorspronkelijke waarnemingen heeft. Handiger om mee te werken is daarom de standaarddeviatie of standaardafwijking: \[\begin{equation*} s_x= \sqrt{s_x^2} . \end{equation*}\]

De standaarddeviatie is gedefinieerd voor elke numerieke variabele, maar is vooral nuttig omdat voor heel wat variabelen (in het bijzonder Normaal verdeelde variabelen - zie Sectie 4.4) bij benadering 68% van de waarnemingen liggen tussen \(\bar{x} - s_x\) en \(\bar{x} + s_x\), en 95% van de waarnemingen liggen tussen¹⁴ \(\bar{x} - 2 s_x\) en \(\bar{x} + 2 s_x\). Deze intervallen noemt men respectievelijk 68% en 95% referentie-intervallen. Het is precies deze eigenschap die de standaarddeviatie zo nuttig maakt in de praktijk. De standaarddeviatie van een reeks waarnemingen wordt vaak afgekort als SD in de wetenschappelijke literatuur.

Eigenschap

Als alle uitkomsten \(x_i\) met een willekeurige constante \(a\) worden vermenigvuldigd, dan wordt hun variantie vermenigvuldigd met \(a^2\) en hun standaarddeviatie met \(|a|\) (de absolute waarde van \(a\)). Als bij alle uitkomsten \(a\) wordt opgeteld, wijzigen hun variantie en standaarddeviatie niet.

Einde eigenschap

# Het gebruik van functie sd() levert de standarddeviatie
# van de variabele BMI in de NHANES dataset.
# Het na.rm=TRUE argument wordt gebruikt omdat er
# ontbrekende waarnemingen voorkomen.
sd(NHANES$BMI,na.rm=TRUE)

## [1] 7.376579

 # levert de variantie van de variabele BMI
var(NHANES$BMI,na.rm=TRUE)

## [1] 54.41392

Wanneer een variabele niet Normaal verdeeld is (dit is bijvoorbeeld het geval voor het BMI gezien het niet symmetrisch verdeeld is), dan geldt niet langer dat bij benadering 95% van de waarnemingen ligt tussen \(\bar{x} - 2 s\) en \(\bar{x} + 2 s\). Een symmetrische maat voor de spreiding van de gegevens, zoals de standaarddeviatie, is dan niet langer interessant. In dat geval zijn de range en interkwantielafstand betere maten.

Definitie 4.8 (bereik en interkwartielafstand) Het bereik of de range \(R_x\) van een reeks waarnemingen \(x_i, i=1,2,...,n\), is per definitie het verschil tussen de grootste en kleinste geobserveerde waarde. De interkwartielafstand van een reeks waarnemingen \(x_i, i=1,2,...,n\) is per definitie de afstand tussen het derde kwartiel \(x_{75}\) en het eerste kwartiel \(x_{25}\). Dat wordt ook grafisch weergegeven op een boxplot (breedte van de box). Hierbinnen liggen circa 50% van de observaties. Circa 95% van de observaties kan men vinden tussen het 2.5% en 97.5% percentiel.

Einde definitie

Het bereik is zeer gevoelig voor outliers en is systematisch afhankelijk van het aantal observaties: hoe groter \(n,\) hoe groter men \(R_x\) verwacht. Om die reden vormt een interkwartielafstand een betere maat voor de spreiding van de gegevens dan de range.

Tenslotte is het vaak zo dat de gegevens meer gespreid zijn naarmate hun gemiddelde hogere waarden aanneemt. De variatiecoëfficiënt=\(VC_x\) standaardiseert daarom de standaarddeviatie door ze uit te drukken als een percentage van het gemiddelde \[\begin{equation*} VC_x = \frac{s_x}{\bar{x}} 100\%. \end{equation*}\]

Omdat ze gestandaardiseerd is, dient ze beter dan de standaarddeviatie zelf om de spreiding op de gegevens te vergelijken tussen populaties met een verschillend gemiddelde. De variatiecoëfficiënt heeft verder de aantrekkelijke eigenschap dat ze geen eenheden heeft en ongevoelig is voor herschaling van de gegevens (d.w.z. wanneer alle gegevens met een constante \(a\) worden vermenigvuldigd, dan is \(VC_{ax}=VC_x\)).

4.4 De Normale benadering van gegevens

Bij biologische en chemische data is het vaak zo dat het histogram van een continue meting bij verschillende subjecten de karakteristieke vorm heeft van de Normale verdeling, die geïllustreerd wordt in Figuur 4.8 (linksboven). Dat is bijvoorbeeld zo als men een histogram maakt van het logaritme van de totale cholestorol. Rond 1870 opperde de wereldberoemde Belg Adolphe Quetelet (die tevens de eerste student was die een doctoraat behaalde aan de Universiteit Gent) de idee om deze curve als `ideaal histogram’ te gebruiken voor de voorstelling en vergelijking van gegevens. Dit zal handig blijken om meer inzicht te krijgen in de gegevens op basis van een minimum aantal samenvattingsvatten, zoals het gemiddelde en de standaarddeviatie die vaak in wetenschappelijke rapporten vermeld staan.

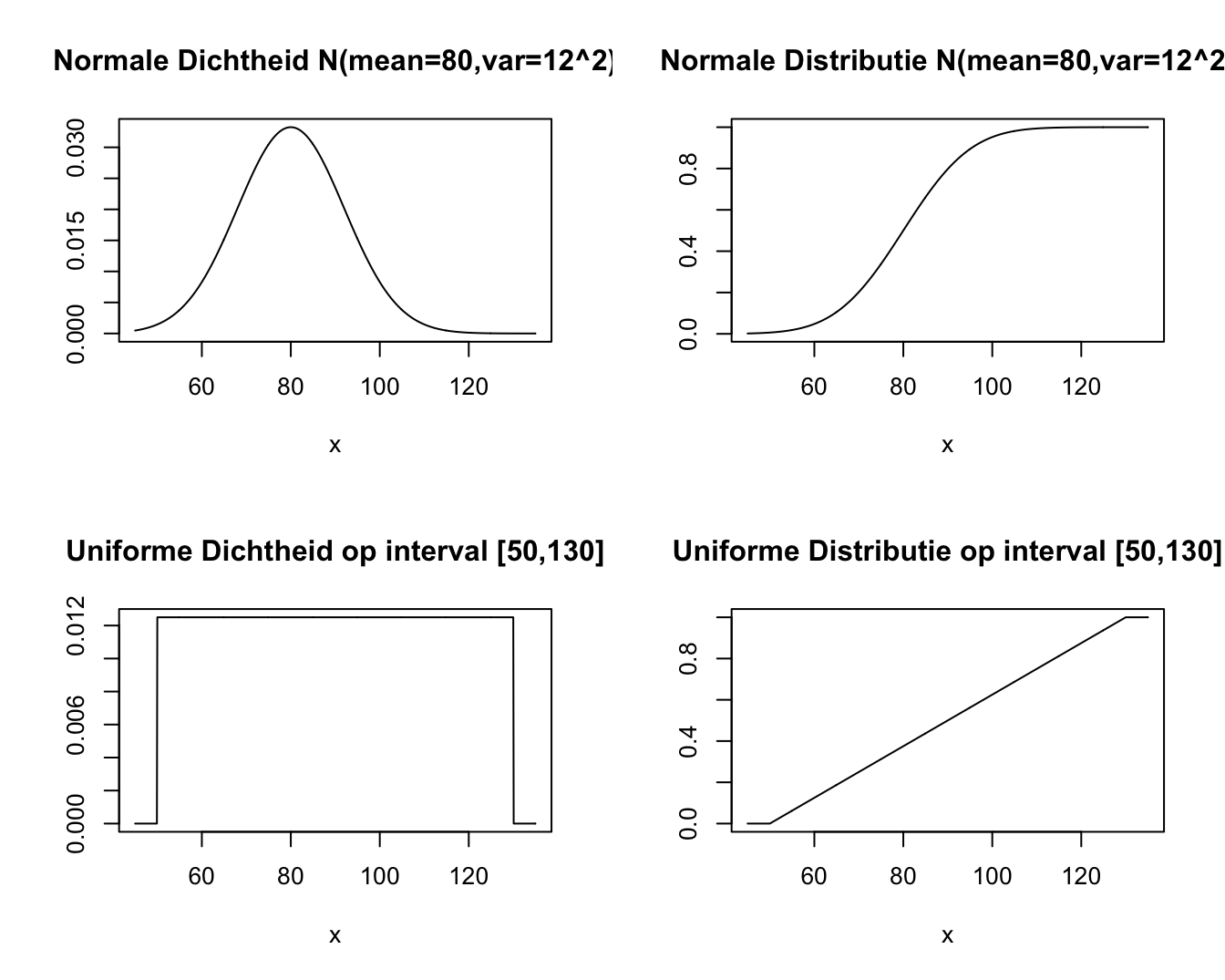
De Normale dichtheidsfunctie (boven, links), de Normale distributiefunctie (boven, rechts), de Uniforme dichtheidsfunctie (onder, links) en de Uniforme distributiefunctie (onder, rechts).

Figuur 4.8: De Normale dichtheidsfunctie (boven, links), de Normale distributiefunctie (boven, rechts), de Uniforme dichtheidsfunctie (onder, links) en de Uniforme distributiefunctie (onder, rechts).

4.4.1 Bepalen van oppervlaktes onder de Normale curve

De Normale curve of Normale dichtheidsfunctie wordt gegeven door: \[\begin{equation*} f(x) = \frac{1}{\sigma \sqrt{2 \pi} } \exp \left ( - \frac{ (x - \mu)^2 }{ 2 \sigma^2} \right ). \end{equation*}\]

Ze wordt beschreven door 2 onbekende parameters \(\mu\) en \(\sigma\), waarbij \(\mu\) het gemiddelde van de verdeling van de observaties aangeeft en \(\sigma\) de standaarddeviatie. Deze curve geeft voor elke waarde \(x\) weer hoe frequent deze waarde, relatief gezien, voorkomt. De notatie \(\pi\) verwijst naar het getal \(\pi=3.1459...\) Wanneer het gemiddelde 0 is en de variantie 1, spreekt men van de standaardnormale curve of standaardnormale dichtheidsfunctie.

Een lukrake observatie uit een reeks gegevens wiens verdeling de Normale curve volgt, wordt een Normaal verdeelde observatie genoemd. Dergelijke observaties komen frequent voor: voor heel wat reeksen gegevens die symmetrisch verdeeld zijn, vormt de Normale curve met \(\mu\) gelijk aan \(\bar x\) en \(\sigma\) gelijk aan \(s_x\) immers een goede benadering voor het histogram.

Voor Normaal verdeelde gegevens geeft de oppervlakte onder de Normale curve tussen 2 willekeurige getallen \(a\) en \(b\) het percentage van de observaties weer dat tussen deze 2 getallen gelegen is. Op die manier laat de Normale curve toe om, enkel op basis van kennis van het gemiddelde en de standaarddeviatie, na te gaan welk percentage van de gegevens bij benadering tussen 2 willekeurige getallen \(a\) en \(b\) gelegen is.

Om deze berekening uit te voeren, gaan we als volgt te werk. Zij \(X\) een lukrake meting uit een reeks Normaal verdeelde gegevens met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\). Dan noteren we met \(P(X\leq b)\) de oppervlakte onder de Normale curve die links van \(b\) gelegen is, en met \(P(a\leq X\leq b)\) de oppervlakte onder de Normale curve tussen \(a\) en \(b\). Hierbij is¹⁵ \[\begin{equation*} P(a\leq X\leq b)=P(X\leq b)-P(X\leq a) \end{equation*}\]

Om \(P(a\leq X\leq b)\) te berekenen, hebben we dus enkel een strategie nodig om voor een willekeurig getal \(x\), het getal \(F(x) = P(X \leq x)\) uit te rekenen. Dit staat uitgezet in functie van \(x\) in Figuur 4.8 (rechtsboven) voor \(\mu=80\) en \(\sigma=12\) en wordt een distributiefunctie genoemd.

Definitie 4.9 (distributiefunctie) De functie die voor elk getal \(x\) uitdrukt wat de kans is dat een lukrake meting \(X\) met gekende verdeling (bvb. een Normale verdeling) kleiner of gelijk is aan \(x\), wordt de distributiefunctie van die verdeling genoemd.

Einde definitie

Omdat de Normale dichtheidsfunctie zeer complex is, blijkt dat het getal \(F(x)\) niet expliciet uit te rekenen is. Om die reden heeft men de getallen \(F(x)\) voor de standaardnormale verdelingsfunctie getabuleerd. Voor deze standaardnormale curve duidt men voor een willekeurige waarde \(z\), het getal \(F(z)\) met \(\Phi(z)\) aan. Omwille van de symmetrie rond 0 van de standaardnormale curve kan de waarde van \(\Phi(-z)\) dan uit de waarde van \(\Phi(z)\) worden afgeleid als \[\begin{equation*} \Phi(-z)= 1- \Phi(z) \end{equation*}\]

Deze uitdrukking geeft aan dat voor een reeks standaardnormaal verdeelde metingen, het percentage dat kleiner is dan \(-z\) gelijk is aan het percentage dat groter is dan \(z\).

Om nu \(P(a\leq X\leq b)\) te berekenen op basis van de tabellen voor de standaardnormale verdeling gaan we als volgt te werk. Vooreerst kan men aantonen dat het resultaat van een lineaire transformatie \(aX+b\) op een Normaal verdeelde meting \(X\) met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\) terug een Normaal verdeelde meting toevalsveranderlijke is, maar nu met gemiddelde \(a\mu+b\) en standaarddeviatie \(|a|\sigma\). Op die manier kan men elke Normaal verdeelde meting met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\) omzetten naar een standaardnormale meting door ze als volgt te standaardiseren: \[\begin{equation*} Z = \frac{X- \mu}{\sigma} \end{equation*}\]

Verifieer dat \(Z\) inderdaad gemiddelde 0 en standaarddeviatie 1 heeft!

Aangezien voor een willekeurig getal \(x\) \[\begin{equation*} X\leq x \Leftrightarrow \frac{X-\mu}{\sigma} \leq \frac{x-\mu}{\sigma} \end{equation*}\] vinden we nu dat \[\begin{eqnarray*} P(a \leq X \leq b) & = & P\left(\frac{a-\mu}{\sigma} \leq Z \leq \frac{b-\mu% }{\sigma} \right) \\ & = & \Phi \left (\frac{b-\mu}{\sigma} \right ) - \Phi \left (\frac{a-\mu}{% \sigma} \right ) \end{eqnarray*}\]

De getallen \(\Phi \left (\frac{b-\mu}{\sigma} \right )\) en \(\Phi \left (\frac{a-\mu}{\sigma} \right )\) kunnen hierbij rechtstreeks uit tabellen of R software worden gehaald. In het vervolg zullen we algemeen de notatie \(Z\) gebruiken om een standaardnormaal verdeelde meting aan te duiden.

Oefening 4.1

Een labo bepaalt in een visstaal Hg via een methode op basis van AAS. In werkelijkheid bevat het staal (gemiddeld) 1.90 ppm. De meetmethode is echter niet perfect, zoals aangegeven door een standaarddeviatie van 0.10 ppm. Wat is de kans dat de laborant die het staal onderzoekt, een meetresultaat van 2.10 ppm of meer vaststelt?

Om op deze vraag te antwoorden, noteren we met \(X\) het meetresultaat van de laborant en berekenen we \[\begin{eqnarray*} P(X\geq 2)&=&P\left(\frac{X-\mu}{\sigma}\geq \frac{2.1-1.9}{0.1}\right) \\ &=&P(Z\geq 2) = 2.28\% \end{eqnarray*}\]

We besluiten dat er 2.28% kans is dat de laborant een meetresultaat van minstens 2.10 ppm zal vaststellen. In R kan dit resultaat als volgt bekomen worden:

1 - pnorm(2.1, mean = 1.9, sd = 0.1)

## [1] 0.02275013

waarbij de functie pnorm de distributiefunctie van de Normale verdeling voorstelt.

**Einde oefening**

Met \(z_{\alpha}\) duiden¹⁶ we die waarde aan waar \(\alpha100\%\) van de oppervlakte onder de standaardnormale curve rechts van zit; m.a.w. waarvoor geldt dat \(P(Z \geq z_{\alpha}) = \alpha\). Als \(Z\) een standaardnormaal verdeelde meting is, dan stelt \(z_{\alpha}\) bijgevolg het \((1-\alpha)100\%\) percentiel van die verdeling voor. Voor \(z_{\alpha/2}\) geldt dat \(P(-z_{\alpha/2}\leq Z \leq z_{\alpha/2}) = 1-\alpha\). Bijvoorbeeld, \(P( - z_{0.025}\leq Z \leq z_{0.025}) = 95\%\). Voor een reeks standaardnormaal verdeelde metingen bevat het interval \([-z_{\alpha/2},z_{\alpha/2}]\) dus \((1-\alpha)100\%\) van de observaties.

Stel dat \(X\) een Normaal verdeelde meting is met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\). Dan geldt dat \[\begin{equation*} P\left( - z_{\alpha/2}\leq \frac{X - \mu}{\sigma} \leq z_{\alpha/2}\right) = 1-\alpha . \end{equation*}\] Hieruit volgt dat \[\begin{equation*} P( \mu - z_{\alpha/2} \sigma \leq X \leq \mu + z_{\alpha/2} \sigma ) = 1-\alpha . \end{equation*}\]

Voor een reeks Normaal verdeelde metingen met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\) bevat het interval \([\mu-z_{\alpha/2}\sigma,\mu+z_{\alpha/2}\sigma]\) dus \((1-\alpha)100\%\) van de observaties. In de praktijk worden de parameters \(\mu\) en \(\sigma\) hierbij vervangen door \(\bar x\) en \(s_x\).

Het resulterende interval \([\bar x-z_{\alpha/2}s_x,\bar x+z_{\alpha/2}s_x]\) wordt vaak gebruikt¹⁷, o.a. in de klinische chemie, om referentie-intervallen te berekenen voor een test ter opsporing van een bepaalde pathologie. Eenmaal zo’n referentie-interval, ook wel normaal interval genoemd, werd bepaald, wordt het testresultaat van een patiënt met de vermoede pathologie vergeleken met het interval. Een resultaat buiten het interval is dan indicatief voor de aanwezigheid van de pathologie.

Bij het bepalen van referentie-intervallen is het noodzakelijk om de methode eerst te testen bij mensen zonder de pathologie in kwestie. Voor dit doel worden `normale en gezonde vrijwilligers’ aangezocht. Vaak worden hiertoe collega’s genomen uit het laboratorium dat de test heeft ontwikkeld, hoewel dit allesbehalve ideaal is. Immers, mensen die in een zelfde laboratorium werken, zijn blootgesteld aan dezelfde werkomgeving, die op zijn beurt een invloed kan hebben op hun bloedsamenstelling. Bijgevolg is de bloedsamenstelling van de studiepersonen mogelijks niet representatief voor een normale, gezonde populatie, hetgeen kan leiden tot vertekende referentie-intervallen. In deze cursus zullen we een referentie-interval meer algemeen als volgt definiëren.

Definitie 4.10 (referentie-interval) Een \((1-\alpha)100\%\) referentie-interval voor een veranderlijke \(X\) (bvb. albumine-concentratie in het bloed) in een gegeven studiepopulatie (bvb. volwassen Belgen onder de 60 jaar) is een interval dat zó gekozen werd dat het met \((1-\alpha)100\%\) kans de observatie voor een lukraak individu uit die populatie bevat. Voor een Normaal verdeelde veranderlijke \(X\) met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\) kan dit berekend worden als \[\begin{equation*} [\mu-z_{\alpha/2}\sigma,\mu+z_{\alpha/2}\sigma] \end{equation*}\] en geschat worden op basis van een lukrake steekproef als \[\begin{equation*} [\bar x-z_{\alpha/2}s_x,\bar x+z_{\alpha/2}s_x] \end{equation*}\]

Einde definitie

Voorbeeld 4.3 (Referentie-intervallen)

In het Hoofdstuk 5 statistische besluitvorming handelt de centrale dataset rond een studie naar het effect van het toedienen van een bloeddrukverlagend middel captopril. Alvorens de studie aan te vangen dient men eerst een grenswaarde voor normale bloeddrukwaarden op te stellen om subjecten met normale bloeddrukken van patiënten met hypertensie te kunnen onderscheiden. We zullen hiervoor gebruik maken van een subset van de NHANES studie. In Figuur 4.9 links wordt een histogram gegeven van alle bloeddruk waarden voor subjecten tussen de 40 en 65 jaar. Rechts wordt het histogram weergegeven voor gezonde subjecten tussen de 40 en 65 jaar, waarbij gezonde personen werden geselecteerd op basis van hun BMI klasse, rokers, status algemene gezondheidsstatus, slaapproblemen, of ze aan diabetes lijden en ze in het verleden hard drugs gebruikten.

#verwijderen van alle subjecten met ontbrekende waarnemingen
NHANES2=subset(NHANES,!is.na(Race1)&!is.na(Smoke100n)&!is.na(BMI_WHO)%in%!is.na(Age)&!is.na(HardDrugs)&!is.na(HealthGen)&!is.na(Gender)&!is.na(AlcoholYear)&!is.na(BPSys1)&!is.na(BPSys2)&!is.na(BPSys3)&!is.na(SleepTrouble))
NHANES2$bpSys=rowMeans(NHANES2[,c(27,29,31)])
#subset van de personen tussen 40 en 65 jaar
nhanesSub=subset(NHANES2, Age<=65&Age>=40 &!duplicated(ID) )
#De == operator resulteert in een bolean (FALSE of TRUE)
# de & operater is een logische AND

#subset van gezonde personen
nhanesSubHealthy=subset(nhanesSub,Smoke100n=="Non-Smoker"&Diabetes=="No"&as.double(BMI_WHO)%in%c(2,3)&HardDrugs=="No"&HealthGen!="Poor"&SleepTrouble=="No")
par(mfrow=c(1,2))
hist(nhanesSub$bpSys,xlab="Systolische bloeddruk (mm Hg)",main="Personen tussen 40-65 jaar")
hist(nhanesSubHealthy$bpSys,xlab="Systolische bloeddruk (mm Hg)",main="Gezonde personen tussen 40-65 jaar")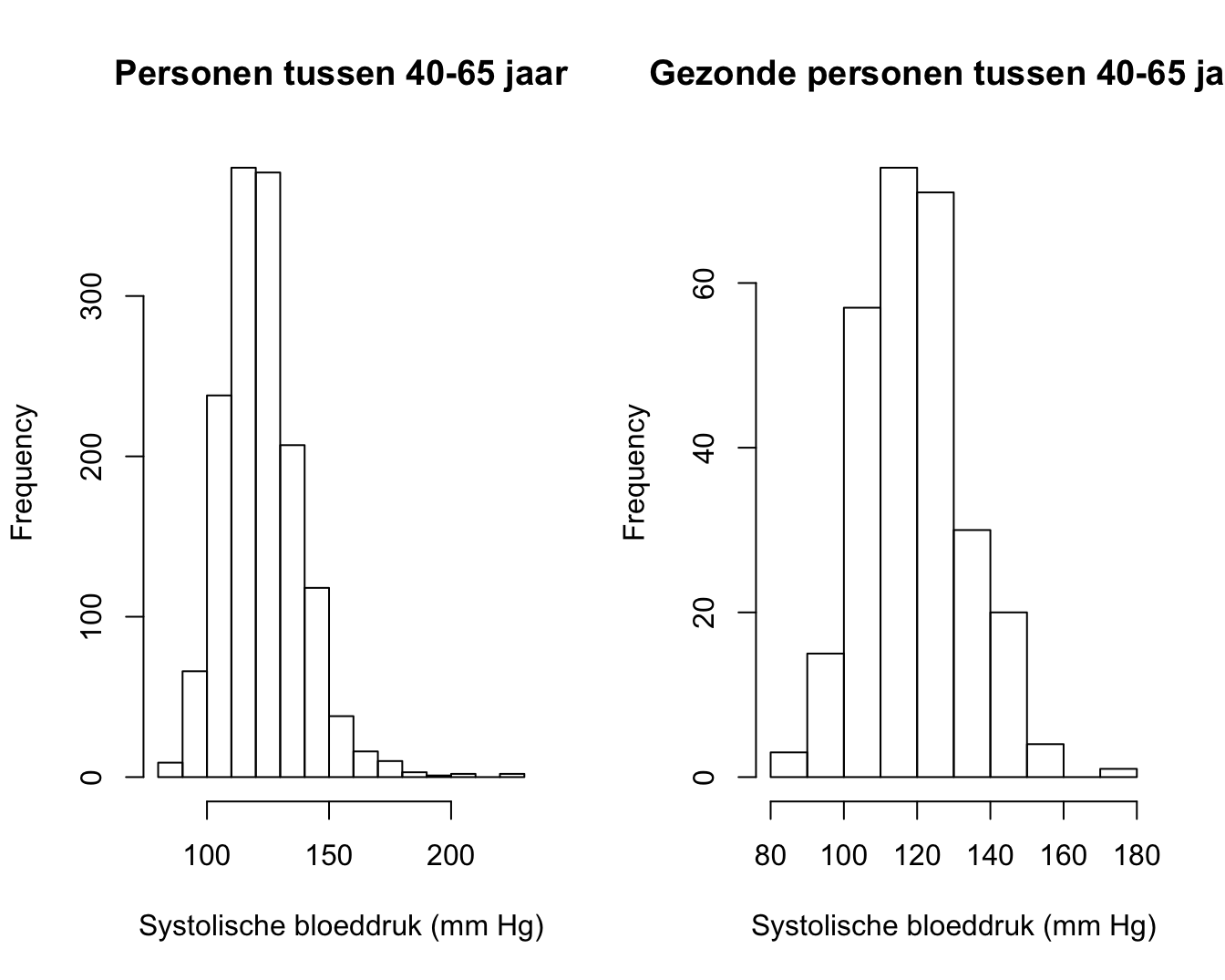

Figuur 4.9: Systolische bloeddruk bij personen tussen de 40 en 65 jaar oud.

De systolische bloeddruk voor gezonde personen is symmetrisch en we zullen later aantonen dat deze approximatief normaal verdeeld zijn. Als het gemiddelde en de standard deviatie van de bloeddruk in de populatie gekend zijn kunnen we normale bloeddrukwaarden afleiden. In de praktijk zijn deze typisch niet gekend en worden deze geschat op basis van de data. In de gezonde subset is het steekproefgemiddelde 119.5mmHg en de standaarddeviatie 14.1mmHg. Als we het populatiegemiddelde en het populatiestandaarddeviatie door deze schattingen vervangen dan bekomen we volgend referentie interval: [91.9, 147]mmHg.

Merk ook op dat de bovengrens van de normale systolische bloeddruk iets boven de grens van hypertensie van 140 mmHg ligt die in de literatuur wordt gehanteerd.

**Einde voorbeeld**

mean(nhanesSubHealthy$bpSys)+qnorm(c(0.025,0.975))*sd(nhanesSubHealthy$bpSys)

## [1]  91.88971 147.03393

4.4.2 QQ-plots

Hoewel heel wat metingen in de biologische wetenschappen en scheikunde, zoals concentraties van een bepaalde stof, scheef verdeeld zijn naar rechts, worden ze door het nemen van een logaritme vaak getransformeerd naar gegevens waarvoor het histogram de vorm heeft van een Normale dichtheidsfunctie. Dit is uiteraard niet altijd zo en stappen om te verifiëren of observaties Normaal verdeeld zijn, zijn daarom van groot belang om de technieken in Sectie 4.4.1 te kunnen gebruiken, alsook heel wat technieken uit de verdere hoofdstukken die er zullen van uit gaan dat de gegevens Normaal verdeeld zijn. Hoewel een vergelijking van het histogram van de gegevens met de vorm van de Normale curve wel inzicht geeft of de gegevens al dan niet Normaal verdeeld zijn, is dit vaak niet makkelijk te zien en wordt de uiteindelijke beslissing nogal makkelijk beïnvloed door de keuze van de klassebreedtes op het histogram. Om die reden zullen we kwantielgrafieken gebruiken die duidelijker toelaten om na te gaan of gegevens Normaal verdeeld zijn.

QQ-plots of kwantielgrafieken (in het Engels: quantile-quantile plots) zijn grafieken die toelaten te verifiëren of een reeks observaties lukrake trekkingen zijn uit een Normale verdeling. Met andere woorden, ze laten toe om na te gaan of een reeks observaties al dan niet de onderstelling tegenspreken dat ze realisaties zijn van een reeks Normaal verdeelde gegevens. Het principe achter deze grafieken is vrij eenvoudig. Verschillende percentielen die men heeft berekend voor de gegeven reeks observaties worden uitgezet t.o.v. de overeenkomstige percentielen die men verwacht op basis van de Normale curve. Als de onderstelling correct is dat de gegevens Normaal verdeeld zijn, dan komen beide percentielen telkens vrij goed met elkaar overeen en verwacht men bijgevolg een reeks puntjes min of meer op een rechte te zien (zoals in Figuur 4.10, rechtsboven). Systematische afwijkingen van een rechte wijzen op systematische afwijkingen van Normaliteit. Lukrake afwijkingen van een rechte kunnen het gevolg zijn van toevallige biologische variatie en zijn daarom niet indicatief voor afwijkingen van Normaliteit. We gebruiken hiervoor de functie qqPlot uit het package car. De qqPlot functie geeft op de figuur ook banden weer waarbinnen punten uit de normaal verdeling met een kans van 95% kunnen worden verwacht.

## [1]  60 235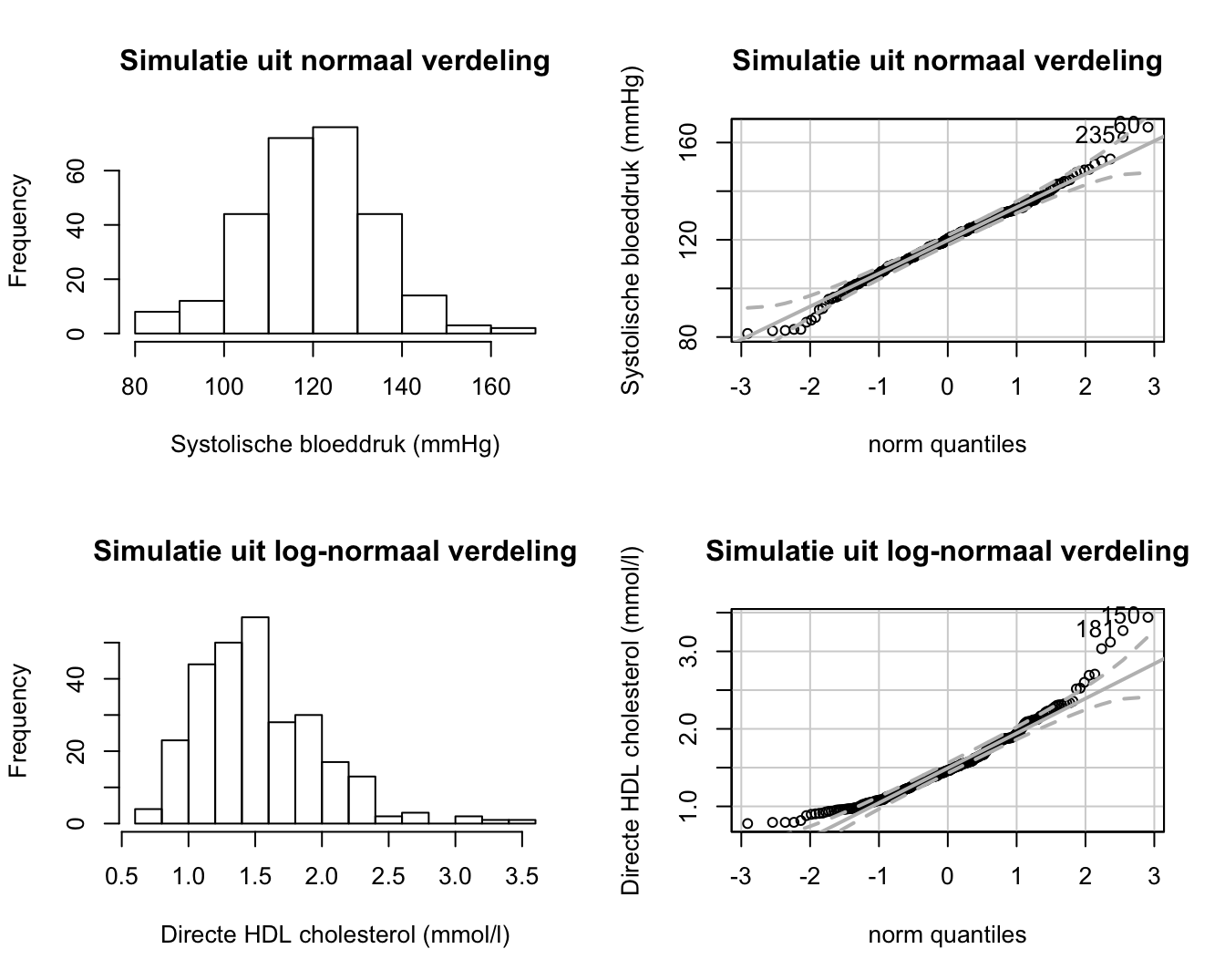

Figuur 4.10: Histogrammen (links) en bijhorende kwantielgrafieken (rechts) voor een aantal verdelingen.

## [1] 150 181

Het berekenen van de percentielen die men verwacht op basis van de Normale curve verloopt vrij eenvoudig. Beschouw bijvoorbeeld \(4n-1\) geordende observaties \(x_1,...,x_{4n-1}\). Dan is \(x_{2n}\) de bijhorende mediaan en is \(\mu\) de mediaan die men verwacht voor een Normaal verdeelde meting met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\). Analoog is \(x_n\) het \(25\%\)-percentiel van de gegeven reeks observaties en is \(\mu-z_{0.25}\sigma=\mu-0.674\sigma\) het \(25\%\)-percentiel dat men verwacht voor een Normaal verdeelde meting met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\). Algemeen is voor \(k=1,...,4n-1\) en \(p=k/4n\), \(x_k\) het \(p 100\%\)-percentiel van de gegeven reeks observaties en \(\mu-z_{p}\sigma\) het overeenkomstige \(p 100\%\)-percentiel van een Normaal verdeelde meting met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\). Omdat \(\mu\) en \(\sigma\) ongekend zijn, kiest men er meestal voor om de percentielen voor de gegeven reeks observaties uit te zetten t.o.v. de gestandaardiseerde percentielen voor de Normale verdeling. Men bekomt deze laatste door de percentielen \(\mu-z_{p}\sigma\), die berekend werden voor de Normale verdeling, te standaardiseren. Aldus bekomt men een grafiek waar men voor elke \(k=1,...,4n-1\) het percentiel \(x_k\) uitzet t.o.v. \(-z_{p}=z_{1-p}\) met \(p=k/4n\). Het resultaat wordt voor een aantal fictieve datasets weergegeven in Figuur 4.10 (rechts) en noemt men een QQ-plot.

De gegevens in Figuur 4.10, rij 1, zijn met een computer gesimuleerd als lukrake trekkingen uit een grote reeks Normaal verdeelde observaties. Zoals verwacht liggen de gegevens in bijhorende QQ-plot nagenoeg op een rechte lijn. Door toevallige variatie is dit geen perfecte rechte lijn, maar kunnen geen systematische afwijkingen van een rechte worden vastgesteld. Dit geeft een suggestie dat de onderstelling van een Normale verdeling hier vermoedelijk voldaan is. In Figuur 4.10 (onder, rechts) stellen we een systematische afwijking van een rechte lijn vast. Op de X-as vinden we de gestandaardiseerde percentielen die worden verwacht voor een Normale verdeling en op de Y-as vinden we de observaties zelf. Merk op dat kleine observaties minder gespreid zijn dan Normaal verdeelde gegevens en dat hoge waarden meer gespreid zijn. Dit wijst erop dat hun verdeling scheef is naar rechts, zoals men ook kan zien op basis van het histogram Figuur 4.10 (onder, links).
Het grote voordeel van een QQ-plot (in vergelijking met een histogram) om afwijkingen van Normaliteit te detecteren, is dat ze dergelijke afwijkingen duidelijker weergeeft dan een histogram.

Hetzelfde principe als voor Normaal verdeelde observaties kan ook herhaald worden voor andere theoretische verdelingen, die we later in deze cursus zullen ontmoeten. Bijvoorbeeld kan men analoge kwantielgrafieken opstellen voor de Poissonverdeling (verdeling voor tellingen) om na te gaan of een reeks observaties lukrake trekkingen vormen uit zo’n Poissonverdeling.

Voorbeeld 4.4 (NHANES vervolg)

## [1] 260 238

## [1] 255  56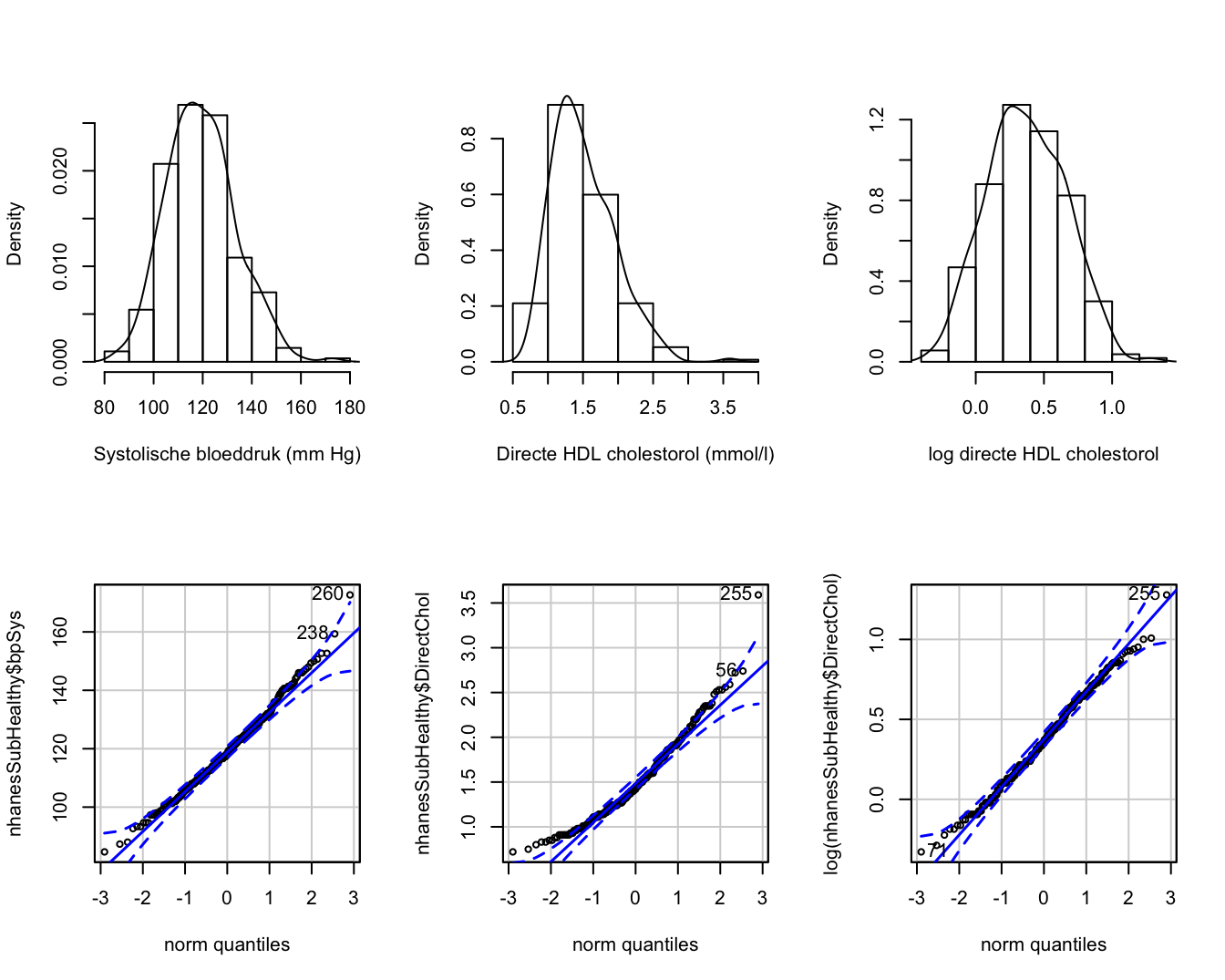

Kernel density schatters (boven) een QQ-plots (onder) voor de systolische bloeddruk en directe HDL cholestorol bij de subset van gezonde personen tussen de 40 en 65 jaar.

Figuur 4.11: Kernel density schatters (boven) een QQ-plots (onder) voor de systolische bloeddruk en directe HDL cholestorol bij de subset van gezonde personen tussen de 40 en 65 jaar.

## [1] 255  71

De QQ-plot in Figuur 4.11 (links onder) geeft aan dat de systolische bloeddruk bij gezonde personen bij benadering Normaal verdeeld is, hetgeen bevestigd wordt door het histogram met de kernel density schatter (links boven).
Op basis van het gemiddelde van 119.5mmHg en de standaarddeviatie van 14.1 mmHg kunnen we aldus besluiten dat 95% van de bloeddruk waarden gelegen zijn tussen de [91.9,147] mmHg.

De QQ-plot in Figuur 4.11 (midden en rechts) geeft aan dat de directe cholestorol bij gezonde personen tussen de 40 en 65 jaar duidelijk scheef verdeeld is en dat de Normale benadering beter wordt na log-transformatie. De log-cholestorol is gemiddeld 0.37 en heeft een standaarddeviatie van 0.29. We kunnen bij benadering stellen dat 95% van de log-bloeddrukken liggen tussen [-0.19,0.93]. Bijgevolg verwachten we benadering 95% van de cholestorol metingen tussen \(\exp(-0.27)=0.76\) en \(\exp(0.85)=2.34\) \(\mu\)mol/l. Deze wijken ietwat af van de overeenkomstige 2.5% en 97.5% percentielen [0.87, 2.52] \(\mu\)mol/l deels doordat steekproefpercentielen minder precies (lees: minder stabiel) zijn dan schattingen die men ervoor bekomt op basis van de Normale verdeling.

**Einde voorbeeld**

4.5 Samenvattingsmaten voor categorische variabelen

De samenvattingsmaten uit de vorige sectie (gemiddelde, mediaan, standaarddeviatie, …) kunnen niet zomaar toegepast worden voor de beschrijving van categorische variabelen. In deze sectie gaan we hier dieper op in, daarbij onderscheid makend tussen enerzijds gegevens die uit prospectieve studies of lukrake steekproeven afkomstig zijn, en anderzijds gegevens uit retrospectieve studies.

4.5.1 Prospectieve studies en lukrake steekproeven

Voorbeeld 4.5 (Houtluizen)

Een bioloog verzamelt `s nachts bladerafval op een lukrake plaats van 1 m\(^2\) in 2 wouden, waarvan 1 met klei- en 1 met kalkgrond. Op elke plaats telt hij het aantal houtluizen van de species Armadilidium of Oniscus, met als doel na te gaan of de ene soort vaker voorkomt op kleigrond dan op kalkgrond¹⁸. Tabel 4.2 toont de bekomen gegevens. Hier stelt \(a\) (\(c\)) het aantal houtluizen van de soort Armadilidium (Oniscus) voor op kleigrond, en \(b\) (\(d\)) het aantal houtluizen van de soort Armadilidium (Oniscus) op kalkgrond.

Tabel 4.2: Kruistabel van species houtluis versus type grond.
	Armadil.	Oniscus	Totaal
Klei	14 (a)	6 (c)	20 (a+c)
Kalk	22 (b)	46 (d)	68 (b+d)
Totaal	36 (a+b)	52 (c+d)	88 (n)

**Einde voorbeeld**

Er zijn verschillende manieren om de resultaten van deze studie te beschrijven. De kans dat 1 van beide species houtluizen van de soort Armadilidium is, is \(p_{kl}=a/(a+c)=0.70\) of 70% op kleigrond en \(p_{ka}=b/(b+d)=0.32\) of 32% op kalkgrond.

Definitie 4.11 (absolute risico verschil) Het absolute risico verschil of absolute kansverschil op een gegeven gebeurtenis (bvb. om Armadilidium aan te treffen) voor populatie T (Test, bvb. kleigrond) versus C (Controle, bvb. kalkgrond) wordt met ARV genoteerd en gedefinieerd als het verschil \[\begin{equation*} ARV=p_T-p_C \end{equation*}\]

tussen de kansen dat deze gebeurtenis zich voordoet in populaties T en C.

Einde definitie

Het ARV op Armadilidium tussen klei- en kalkgrond bedraagt 0.38, hetgeen suggereert dat de kans dat 1 van beide species houtluizen van de soort Armadilidium is, 38% hoger is op kleigrond dan op kalkgrond. Een absoluut kansverschil van 0 drukt uit dat de overeenkomstige kansen even groot zijn in beide populaties en dat beide populaties dus vergelijkbaar zijn in termen van de bestudeerde uitkomst.

Het absolute kansverschil zegt echter niet alles omtrent het bestudeerde effect. Een kansverschil kan immers een grotere impact hebben alnaargelang beide proporties \(p_T\) en \(p_C\) dicht bij 0 of 1 liggen, dan wanneer ze in de buurt van 0.5 liggen. Bijvoorbeeld, wanneer we de proportie vrouwen jonger dan 60 jaar meten die borstkanker ontwikkelen, is een risicoverschil tussen \(p_A=0.01\) voor vrouwen die het allel Leu/Leu bezitten op het BRCA1 gen en \(p_B=0.001\) voor de overige vrouwen, wellicht belangrijker dan een verschil tussen \(p_C=0.41\) en \(p_D=0.401\) voor beide populaties. Een uitspraak dat het risico 0.9% lager is in de ene dan in de andere populatie geeft om die reden slechts een beperkt beeld van het belang van die reductie. Een goede vergelijking van risico’s, kansen of percentages moet om die reden ook rekening houden met het basisrisico (d.w.z. de kans op de bestudeerde uitkomst in een referentiepopulatie). Het ARV doet dit niet, in tegenstelling tot volgende associatiemaat.

Definitie 4.12 (relatief risico) Het relatief risico op een gegeven gebeurtenis (bvb. om Armadilidium aan te treffen) voor populatie T (Test, bvb. kleigrond) versus C (Controle, bvb. kalkgrond) wordt met RR genoteerd en gedefinieerd als het quotiënt \[\begin{equation*} RR=\frac{p_T}{p_C} \end{equation*}\]

van de kansen dat deze gebeurtenis zich voordoet in populaties T en C.

Einde definitie

In de studie naar houtluizen bedraagt dit \(RR=0.70/0.32=2.2\). Dit suggereert dat er 2.2 keer zoveel kans om een houtluis van de soort Armadilidium (i.p.v. Oniscus) aan te treffen op kleigrond dan op kalkgrond. Een relatief risico van 1 drukt uit dat beide populaties dus vergelijkbaar zijn in termen van de bestudeerde uitkomst.

Een nadeel van het relatief risico is dat ze, in tegenstelling tot het absolute risico verschil, niet goed duidelijk maakt hoeveel meer individuen de bestudeerde uitkomst ondervinden in de ene dan in de andere populatie. Bijvoorbeeld, zelfs wetende dat het relatief risico op Armidilidium in klei-versus kalkgrond 2.2 bedraagt, is het niet mogelijk om uit te maken hoeveel meer houtluizen van de soort Armidilidium zich manifesteren op kleigrond. Als de kans om Armidilidium aan te treffen i.p.v. Oniscus 0.1% bedraagt op kalkgrond, dan verwacht men dat er per 10000 houtluizen (van de soort Armidilidium of Oniscus) er 10 van de soort Armidilidium zullen zijn op kalkgrond en 22 op kleigrond, wat neerkomt op een verwaarloosbaar verschil van 12. Als de kans om Armidilidium aan te treffen i.p.v. Oniscus 40% bedraagt op kalkgrond, dan verwacht men dat er per 10000 houtluizen (van de soort Armidilidium of Oniscus) er 4000 van de soort Armidilidium zullen zijn op kalkgrond en 8800 op kleigrond, wat neerkomt op een aanzienlijk verschil van 4800. Soms rapporteert men in de plaats van het relatief risico, het relatieve risico verschil \(ARV/p_C=RR-1\). Voor de gegeven studie bedraagt dit 1.2. Het drukt uit dat de toename (van kalk- naar kleigrond) in kans om Armadilidium aan te treffen succes meer dan 1 keer zo groot is als het basisrisico in de controlegroep (kalkgrond).

Merk op dat alle bovenstaande associatiematen eveneens gebruikt kunnen worden wanneer men, in tegenstelling tot wat in een prospectieve studie gebeurt, een volledig lukrake groep proefpersonen selecteert zonder vast te leggen hoeveel van hen al dan niet blootgesteld zijn.

4.5.2 Retrospectieve studies

Beschouw de case-controle studie uit Voorbeeld 3.16, waarvan de gegevens samengevat zijn in Tabel 4.3. Omdat men in zo’n design op zoek gaat naar \(a+b+c\) lukraak gekozen controles en \(d+e+f\) lukraak gekozen cases, liggen de marges \(a+b+c\) en \(d+e+f\) vast en is het bijgevolg onmogelijk om het risico op case (bvb. risico op borstkanker) te schatten. Dit is noch mogelijk binnen de totale groep, noch binnen de groep van blootgestelden (d.i. vrouwen met allel Leu/Leu), noch binnen de groep niet-blootgestelden. Immers, de kans op case binnen die geobserveerde groep reflecteert hoofdzakelijk de verhouding waarin cases en controles in totaal werden gekozen door het design. Alleen analyses die de kolomtotalen in de tabel vast gegeven veronderstellen, zijn hier zinvol. Dit heeft tot gevolg dat het relatief risico op de aandoening (d.w.z. op case) in de populatie voor blootgestelden versus niet-blootgestelden niet rechtstreeks kan geschat worden op basis van gegevens uit een case-controle studie. Analoog kan ook het bijhorende absolute risicoverschil niet geschat worden.

Tabel 4.3: Kruistabel van borstkanker-status versus BRCA1-allel.
Genotype	Controles	Cases	Totaal
Pro/Pro	266 (a)	342 (d)	608 (a+d)
Pro/Leu	250 (b)	369 (e)	619 (b+e)
Leu/Leu	56 (c)	89 (f)	145 (c+f)
Totaal	572 (a+b+c)	800 (d+e+f)	1372 (n)

Wel heeft men informatie over de kans om het allel Leu/Leu aan te treffen bij cases, \(\pi_1=f/(d+e+f)=89/800=11.1\%\), en de kans op het allel Leu/Leu bij controles, \(\pi_0=c/(a+b+c)=56/572=9.8\%\). Het relatief risico op blootstelling voor cases versus controles is bijgevolg \(11.1/9.8=1.14\). Vrouwen met borstkanker hebben dus 14% meer kans om de allelcombinatie Leu/Leu te hebben op het BRCA1 gen dan vrouwen zonder borstkanker. Dit suggereert dat er een associatie¹⁹ is tussen het polymorfisme op het BRCA1 gen en borstkanker, maar drukt helaas niet uit hoeveel hoger het risico op borstkanker is voor vrouwen met de allelcombinatie Leu/Leu dan voor andere vrouwen. Om toch een antwoord te vinden op deze laatste vraag, voeren we een nieuwe risicomaat in.

Definitie 4.13 (Odds) De odds op een gebeurtenis wordt gedefinieerd als \[\begin{equation*} \frac{p}{1-p} \end{equation*}\]

waarbij \(p\) de kans is op die gebeurtenis.

Einde definitie

De odds is dus een transformatie van het risico, met onder andere de volgende eigenschappen:

de odds neemt waarden aan tussen nul en oneindig.
de odds is gelijk aan 1 als en slechts als de kans zelf gelijk is aan 1/2.
de odds neemt toe als de kans toeneemt.

Het gebruik van odds is populair onder gokkers omdat het uitdrukt hoeveel waarschijnlijker het is om te winnen dan om te verliezen. Een odds op winnen gelijk aan 1 drukt bijvoorbeeld uit dat het even waarschijnlijk is om te winnen dan om te verliezen. Een odds op winnen gelijk aan 0.9 drukt uit men per 10 verliesbeurten, 9 keer verwacht te winnen. In de genetische associatiestudie uit Voorbeeld 3.16 is de odds op allel Leu/Leu bij cases gelijk aan \(\mbox{odds}_1=f/(d+e)=89/711=0.125\) en bij controles gelijk aan \(\mbox{odds}_2=c/(a+b)=56/516=0.109\). Vrouwen met borstkanker hebben bijgevolg ongeveer 8 (\(\approx 1/0.125\)) keer meer kans om de allelcombinatie Leu/Leu niet te hebben op het BRCA1 gen dan om het wel te hebben. Om de associatie tussen blootstelling en uitkomst te beschrijven, kan men nu een verhouding van odds (odds ratio) gebruiken in plaats van een verhouding van risico’s (relatief risico).

Definitie 4.14 (Odds ratio) De odds ratio op een gegeven gebeurtenis (bvb. borstkanker) voor populatie T (bvb. vrouwen met allel Leu/Leu) versus C (bvb. vrouwen zonder allel Leu/Leu) wordt met OR genoteerd en gedefinieerd als het quotiënt \[\begin{equation*} OR=\frac{\mbox{odds}_T}{\mbox{odds}_C} \end{equation*}\]

van de odds op deze gebeurtenis in populaties T en C.

Einde definitie

Op basis van de gegevens in Tabel 4.3 kan de odds ratio op blootstelling voor cases versus controles geschat worden d.m.v. het kruisproduct \[\begin{equation*} \frac{ \frac{ f/(d+e+f)}{(d+e)/(d+e+f)} }{ \frac{c/(a+b+c)}{(a+b)/(a+b+c)}} = \frac{f(a+b)}{c (d+e)} \end{equation*}\]

In het bijzonder vinden we dat de odds op allelcombinatie Leu/Leu voor vrouwen met versus zonder borstkanker gelijk is aan \(OR=(89\times 516)/(56\times 711)=1.15\). Helaas drukt dit resultaat nog steeds niet uit hoeveel meer risico op borstkanker vrouwen met de allelcombinatie Leu/Leu lopen.

Was de bovenstaande studie echter een volledig lukrake steekproef geweest (waarbij het aantal cases en controles niet per design werden vastgelegd), dan konden we daar ook de odds ratio op borstkanker berekenen voor mensen met versus zonder het allel Leu/leu. We zouden dan vaststellen dat dit gelijk is aan \[\begin{equation*} \frac{ \frac{ f/(c+f)}{c/(c+f)} }{ \frac{(d+e)/(a+b+d+e)}{(a+b)/(a+b+d+e)}} = \frac{f(a+b)}{c(d+e)}, \end{equation*}\]

en bijgevolg dezelfde waarde aanneemt. Dat is omdat de odds ratio een symmetrische associatiemaat is zodat de odds ratio op `case’ voor blootgestelden versus niet-blootgestelden steeds gelijk is aan de odds op blootstelling voor cases versus controles. Hieruit volgt dat voor het schatten van de odds ratio het er niet toe doet of we prospectief werken zoals in een typische cohort studie, of retrospectief zoals in een typische case-controle studie. In het bijzonder kunnen we in de genetische associatiestudie uit Voorbeeld 3.16 de odds op borstkanker voor vrouwen met allel Leu/leu versus zonder berekenen als \(OR=89\times 516/(56\times 711)=1.15\). De odds op borstkanker is bijgevolg 15% hoger bij vrouwen met die specifieke allelcombinatie.

Stel nu dat we met \(p_T\) en \(p_C\) respectievelijk de kans op case noteren voor blootgestelden en niet-blootgestelden. Wanneer beide kansen klein zijn (namelijk \(p_T<5\%\) en \(p_C<5\%\)), dan is de odds een goede benadering voor het risico. Dit is omdat in dat geval \(\mbox{odds}_T=p_T/(1-p_T)\approx p_T\) en \(\mbox{odds}_C=p_C/(1-p_C)\approx p_C\). Er volgt dan bovendien dat de odds ratio een goede benadering voor het relatief risico: \[\begin{equation*} OR=\frac{\mbox{ odds}_T}{\mbox{ odds}_C}\approx \frac{p_T}{p_C}=RR \end{equation*}\]

Wetende dat het risico op borstkanker laag is, mogen we op basis van de gevonden OR van 1.15 bijgevolg besluiten dat het risico (i.p.v. de odds) op borstkanker (bij benadering) 15% hoger ligt bij vrouwen met het allel Leu/Leu op het BRCA1 gen. Dit is een bijzonder nuttige eigenschap omdat (a) het relatief risico, dat niet rechtstreeks geschat kan worden in case-controle studies, gemakkelijker te interpreteren is dan de odds ratio; en (b) de odds ratio bepaalde wiskundige eigenschappen heeft die ze aantrekkelijker maakt dan een relatief risico in statistische modellen²⁰. Algemeen is de odds ratio echter steeds verder van 1 verwijderd dan het relatief risico. Wetende dat de odds ratio op borstkanker 1.15 bedraagt voor vrouwen met versus zonder de allelcombinatie Leu/Leu, kunnen we bijgevolg meer nauwkeurig besluiten dat het overeenkomstige relatief risico tussen 1 en 1.15 gelegen is (maar niettemin dicht bij 1.15).

Omdat de odds ratio moeilijker te interpreteren is dan een relatief risico en bijgevolg misleidend kan zijn, valt deze laatste steeds te verkiezen in situaties (zoals prospectieve studies) waar het mogelijk is om het relatief risico in de populatie te schatten. In sommige case-controle studies (nl. matched case-controle studies) wordt voor elke case een controle gezocht die bepaalde karakteristieken gemeenschappelijk heeft, teneinde een betere onderlinge vergelijkbaarheid te garanderen. In dat geval moet de statistische analyse (inclusief de manier om odds ratio’s te schatten) rekening houden met het feit dat de resultaten van elke case gecorreleerd of verwant zijn met de resultaten van de bijhorende controle.

4.5.3 Rates versus risico’s

Vaak wordt het begrip risico verward met het begrip rate. Een rate drukt een aantal gebeurtenissen (bvb. aantal sterfte- of ziektegevallen) uit per eenheid in de populatie in een bepaalde tijdspanne. Bijvoorbeeld, een crude mortality rate (CMR) voor een bepaald jaartal is gedefinieerd als 1000 maal het aantal sterftegevallen dat optreedt in dat jaar gedeeld door de grootte van de beschouwde populatie halfweg dat jaar. De reden dat met 1000 wordt vermenigvuldigd is dat het bijvoorbeeld makkelijker na te denken is over een CMR van 12 sterftes per 1000 in Engeland en Wales, dan over 0.012 sterftes per individu. Indien een specifieke leeftijdsgroep wordt gekozen, verkrijgt men de leeftijdsspecifieke mortality rate als 1000 maal het aantal sterftegevallen dat optreedt in een bepaald jaar en bepaalde leeftijdsgroep gedeeld door de grootte van de beschouwde populatie in die leeftijdsklasse halfweg dat jaar. In tegenstelling tot de incidentie, is de prevalentie geen rate omdat ze niet een aantal gebeurtenissen uitdrukt over een zekere tijdspanne.

4.6 Associaties tussen twee variabelen

Tot nog toe zijn we hoofdzakelijk ingegaan op zogenaamde univariate beschrijvingen waarbij slechts 1 variabele onderzocht wordt. In de meeste wetenschappelijke studies wenst men echter associaties tussen 2 of meerdere variabelen te onderzoeken, bijvoorbeeld tussen een interventie en de daarop volgende respons. In deze Sectie onderzoeken we hoe associaties tussen 2 variabelen kunnen beschreven worden. We maken daarbij onderscheid naargelang het type van de variabelen.

4.6.1 Associatie tussen twee kwalitatieve variabelen

Als twee kwalitatieve variabelen niet veel verschillende waarden aannemen, dan is een kruistabel aangewezen om hun associatie voor te stellen. In deze tabel worden de verschillende waarden die de ene variabele aanneemt in de kolommen uitgezet en de verschillende waarden die de andere variabele aanneemt in de rijen. In elke cel van de tabel (die overeenkomt met 1 specifieke combinatie van waarden voor beide variabelen) wordt de frequentie neergeschreven.

Tabel 4.4: Kruistabel van Gender vs BMI klasse.
	12.0_18.5	18.5_to_24.9	25.0_to_29.9	30.0_plus
female	629	1616	1179	1402
male	648	1295	1485	1349

Tabel 4.4 toont zo’n kruistabel voor het aantal mannen en vrouwen per BMI klasse. Dergelijke eenvoudige kruistabel met slechts 2 rijen en 4 kolommen, noemt men ook een \(2\times 4\) tabel.

4.6.2 Associatie tussen één kwalitatieve en één continue variabele

De eenvoudigste grafische weergave met het maximum aan informatie om de associatie tussen een kwalitatieve en een continue variabele te beschrijven is een dot-plot.

ggplot(NHANES[1:100,], aes(x = Gender, y = log(DirectChol))) +
  geom_dotplot(binaxis = "y", stackdir = "center")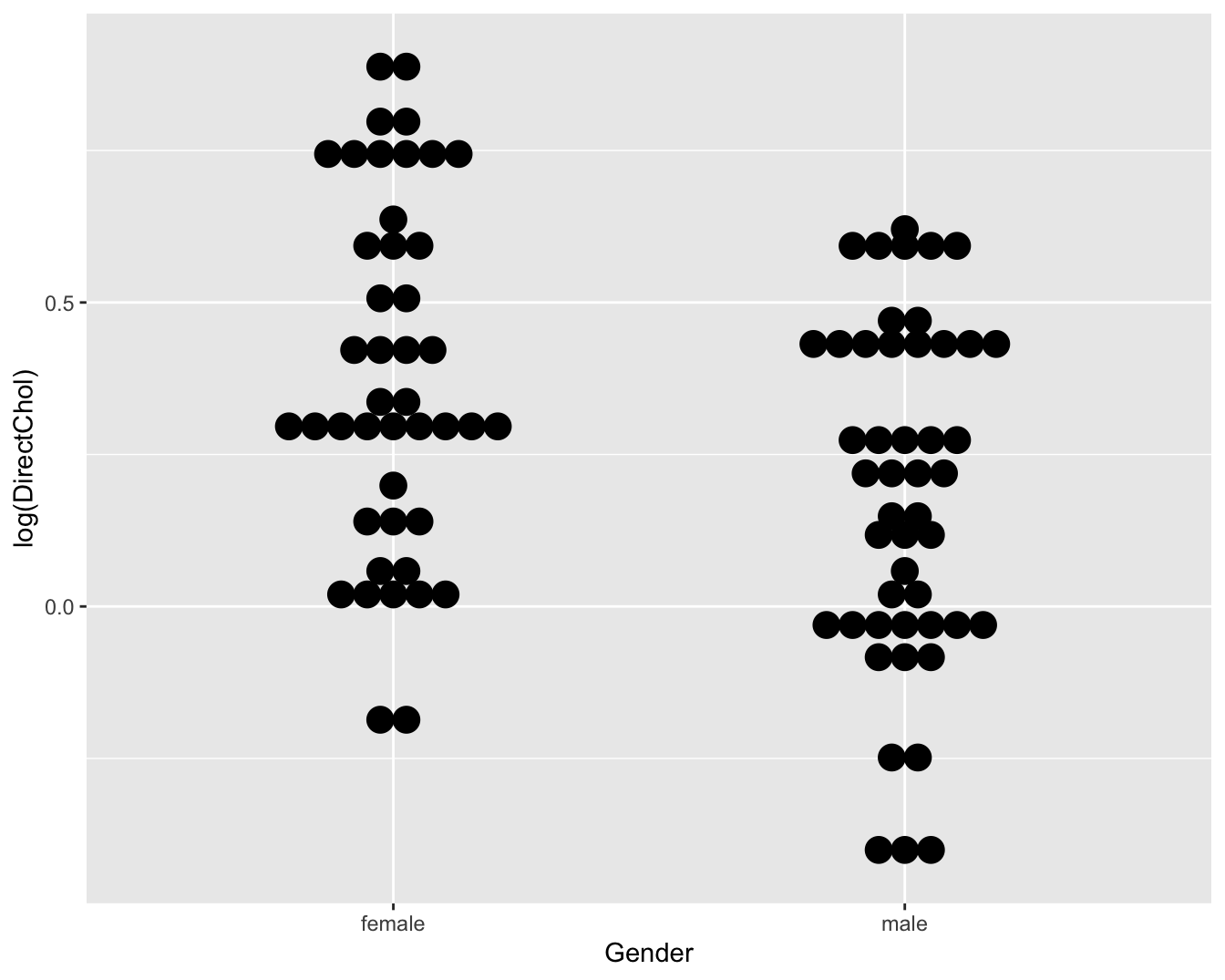

Dotplot van log-getransformeerde directe HDL cholestorol concentratie in functie van Gender voor de eerste 100 subjecten van de NHANES studie.

Figuur 4.12: Dotplot van log-getransformeerde directe HDL cholestorol concentratie in functie van Gender voor de eerste 100 subjecten van de NHANES studie.

Dit wordt geïllustreerd in Figuur 4.12 waarbij de log directe cholestorol concentratie is geplot in functie van het geslacht voor de eerste 100 personen in de studie. Deze voorstellingsmethode behoudt de individuele waarden van de observaties en laat gemakkelijke vergelijkingen toe tussen de verschillende groepen. Een bijkomend voordeel is dat outliers meteen zichtbaar zijn in een dot-plot. Een nadeel ontstaat wanneer de steekproef groot is en bijgevolg vele observaties samenvallen op de figuur. Vandaar dat we de plot hebben gemaakt voor een subset van de data.

Als het aantal observaties groot is, kan een dot-plot vervangen worden door boxplots. Deze is meer compact dan een histogram en laat om die reden gemakkelijker vergelijkingen tussen verschillende groepen toe. Twee dergelijke boxplots worden getoond in Figuur 4.13.

boxplot(log(DirectChol)~Gender,data=NHANES,ylab="log(Direct Cholestorol)")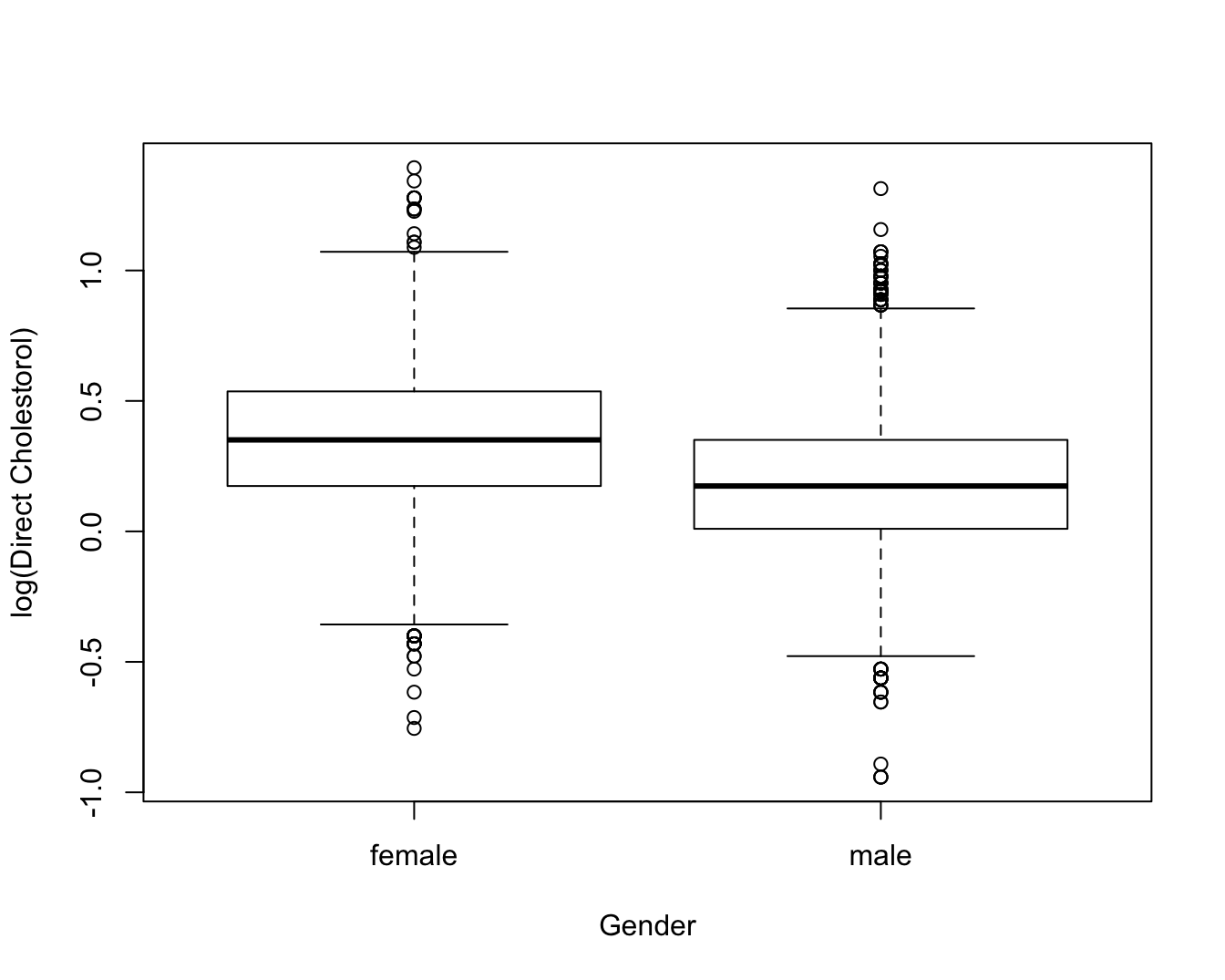

Dotplot van log-getransformeerde directe HDL cholestorol concentratie in functie van Gender voor alle subjecten van de NHANES studie.

Figuur 4.13: Dotplot van log-getransformeerde directe HDL cholestorol concentratie in functie van Gender voor alle subjecten van de NHANES studie.

Op basis van deze figuur stellen we vast dat hogere log-cholestorol concentraties geobserveerd worden bij vrouwen dan bij mannen, maar dat de variabiliteit van de log-concentraties vergelijkbaar is tussen de 2 groepen. De vraag blijft of we hier kunnen spreken van een systematisch hogere log-cholestorol concentratie tussen vrouwen en mannen. We zullen in Hoofdstuk 5 dieper op deze vraag ingaan.

Figuur 4.13 kan men samenvatten door gemiddelde verschillen tussen beide groepen te rapporteren. Hier stellen we een gemiddeld verschil van 0.17 in directe HDL cholestorol concentratie vast op de log schaal tussen vrouwen en mannen. Gezien we weten dat \(\log(C_2)-\log(C_1)=\log(C_2/C_1)\) besluiten we dat de HDL cholestorol concentratie in de NHANES studie gemiddeld 1.19 keer hoger ligt voor vrouwen dan voor mannen.

Dot-plots zijn bijzonder interessant in pre-test post-test designs waar dezelfde subjecten op verschillende tijdstippen worden geobserveerd. In dat geval kunnen de uitkomsten uitgezet worden op de Y-as en de tijdstippen op de X-as, en kunnen de metingen voor eenzelfde subject worden verbonden met een lijn.

Een voorbeeld hiervan is weergegeven in Figuur 4.14. De figuur vat de gegevens samen van de captopril studie die de centrale dataset vormt van Hoofdstuk 5. In de studie wenst men het effect van een bloeddrukverlagend geneesmiddel captopril evalueren. Voor elke patiënt in de studie werd de systolische bloeddruk twee keer gemeten: één keer voor en één keer na de behandeling met het bloeddruk verlagende medicijn captopril. In Figuur 4.14 worden de metingen van dezelfde patiënt met een lijntje verbonden. Hierdoor krijgen we een heel duidelijk beeld van de gegevens. Namelijk, we krijgen een sterke indruk dat de bloeddruk daalt na het toedienen van captopril gezien we bijna voor alle patiënten een daling observeren.

##   id SBPb DBPb SBPa DBPa
## 1  1  210  130  201  125
## 2  2  169  122  165  121
## 3  3  187  124  166  121
## 4  4  160  104  157  106
## 5  5  167  112  147  101
## 6  6  176  101  145   85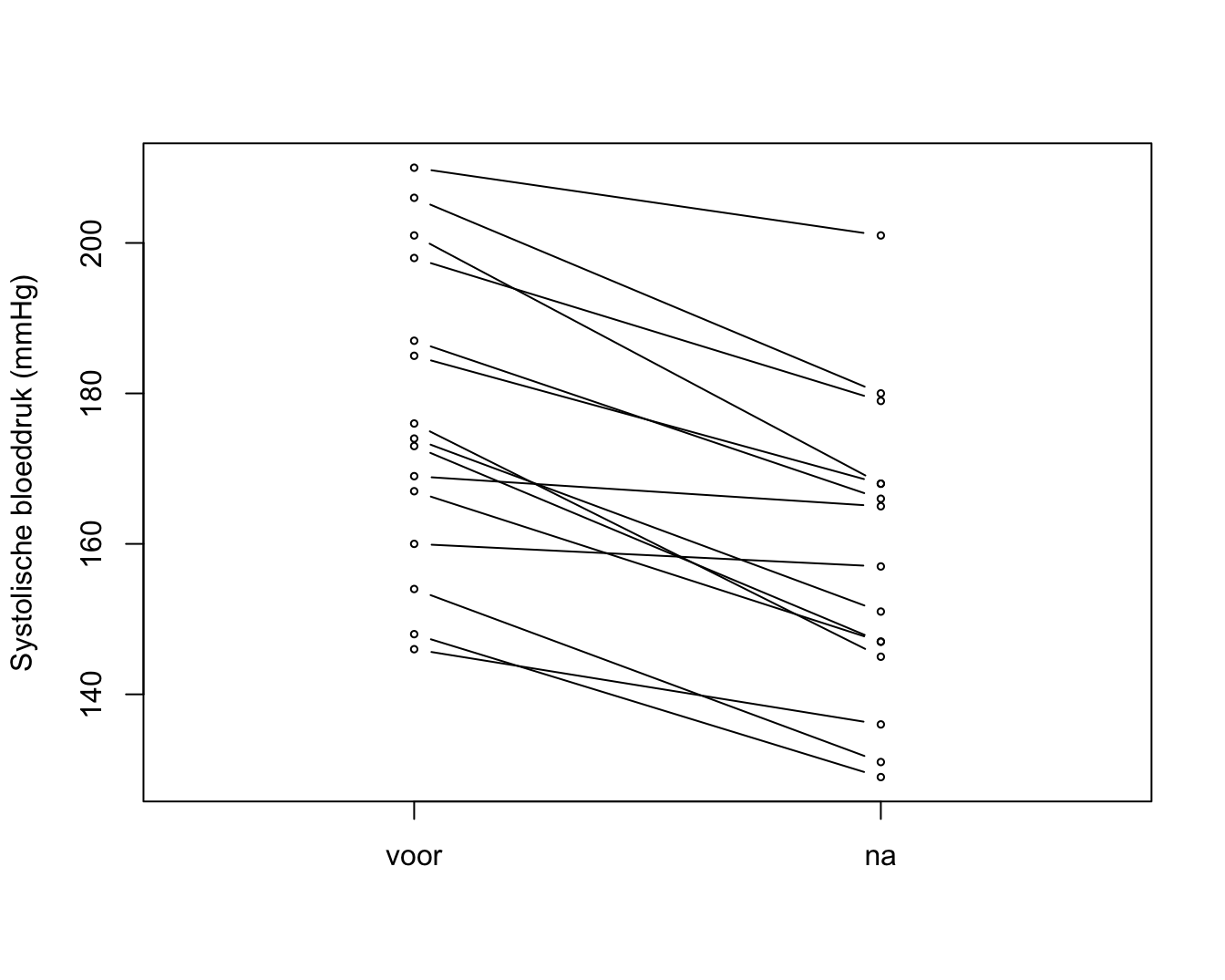

Figuur 4.14: Dotplot van de systolische bloeddruk in de captopril studie voor en na het toedienen van het bloeddruk verlagend middel captopril.

4.6.3 Associatie tussen twee continue variabelen

De associatie tussen 2 kwantitatieve variabelen kan worden onderzocht aan de hand van een puntenwolk of spreidingsdiagram (in het Engels: scatterplot). Hier worden de geobserveerde waarden van de ene variabele uitgezet tegen de andere. In Hoofdstuk 6 wordt gewerkt rond een centrale dataset m.b.t. borstkanker. Voor 32 borstkanker patiënten werd gen-expressie gemeten van de tumor a.d.h.v. microarray technologie. Figuur 4.15 zet de log-expressie uit van het S100A8 gen ten opzichte van estrogen recepter gen (ESR1). Beide genen spelen een belangrijke rol in kanker. Expressie van het ESR1 gen is een indicator dat de tumor vatbaar is voor hormoontherapie wat gunstig is voor de prognose. Het S100A8-gen daarentegen is betrokken bij de onderdrukking van het immuunsysteem en het gen speelt een rol in het creëren van een inflamatoir milieu in de tumor.

borstkanker=read.table("dataset/borstkanker.txt",header=TRUE)
with(borstkanker, scatter.smooth(log2(ESR1),log2(S100A8),lpars=list(lty=2)))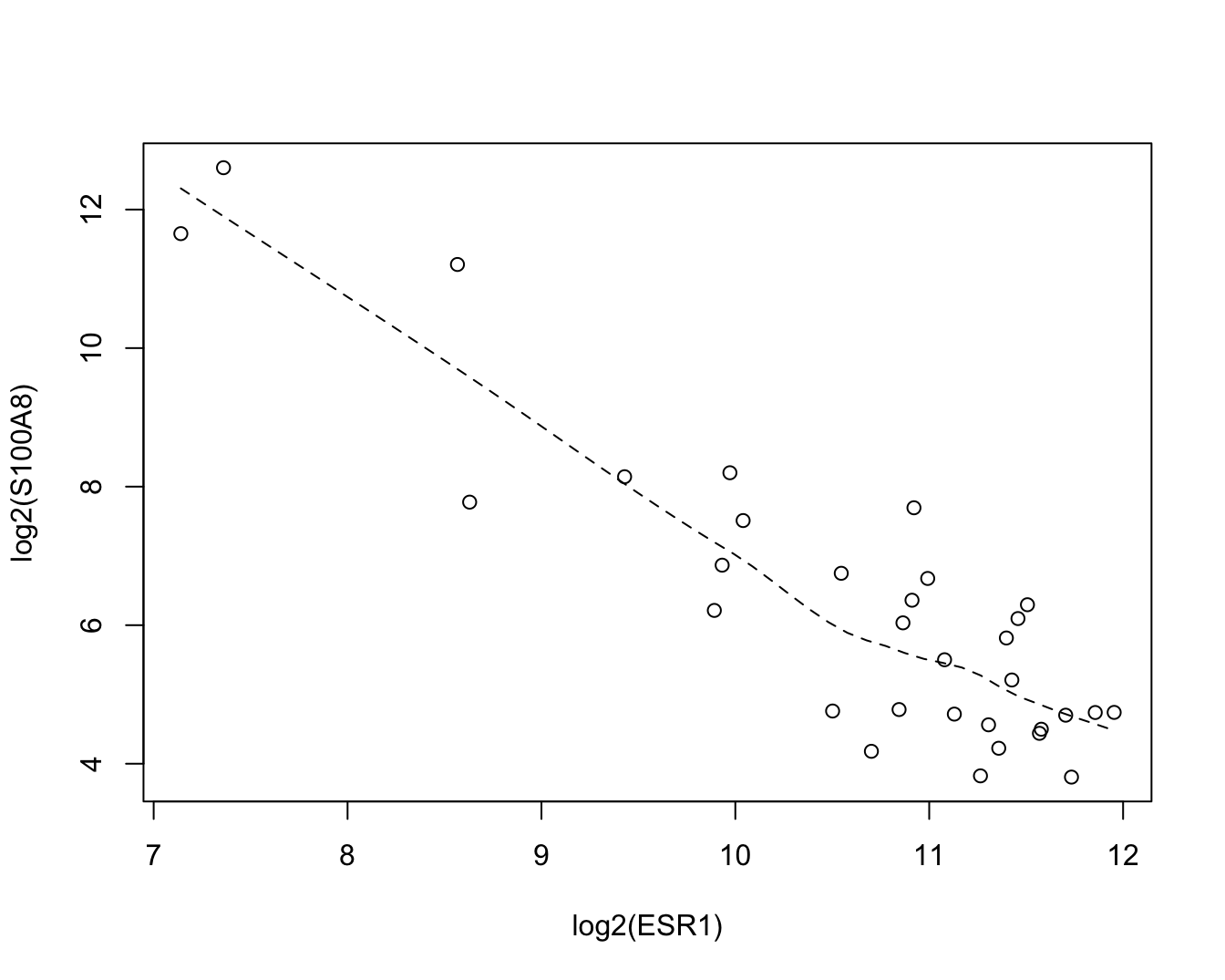

Figuur 4.15: Expressie van het S100A8 gen in functie van de ESR1 gen-expressie.

De lijn op de figuur is een (niet-parametrische) regressielijn. Deze vat de associatie tussen beide variabelen samen door de gemiddelde log2-expressie voor S100A8 weer te geven in functie van de log2-expressie van het ESR1 gen.

We observeren in Figuur 4.15 een negatieve associatie tussen de S100A8 en ESR1 expressie. De expressie van S100A8 neemt gemiddeld gezien af bij patiënten waar het ESR1 gen hoger geëxpresseerd is.

In de praktijk wenst men de sterkte van de samenhang tussen 2 continue variabelen graag ook beknopt uit te kunnen drukken d.m.v. een samenvattingsmaat. Zo’n veelgebruikte maat om de lineaire samenhang tussen 2 continue metingen uit te drukken, is de (Pearson) correlatiecoëfficiënt of kortweg correlatie.

Definitie 4.15 (Correlatie) Stel dat \(x_{i}\) (bvb. lengte) en \(y_{i}\) (bvb. gewicht) 2 metingen zijn die opgemeten werden bij eenzelfde individu \(i=1,...,n\). Dan wordt de Pearson correlatie tussen de rij getallen \(x\) en \(y\) gedefinieerd als: \[\begin{equation*} \mbox{Cor}(x,y)=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{ (n-1)s_{x}s_{y}}, \end{equation*}\]

met \(s_{x}\) en \(s_{y}\) de standaarddeviatie van respectievelijk de rij getallen \(x\) en \(y\). De Pearson correlatie wordt typisch met \(r\) genoteerd.

Einde definitie

De teller in bovenstaande uitdrukking gaat na in welke mate positieve (negatieve) afwijkingen tussen \(x\) en zijn gemiddelde samengaan met positieve of negatieve afwijkingen tussen \(y\) en zijn gemiddelde. Het teken van de correlatie geeft bijgevolg de richting van de lineaire trend aan: het teken is positief (negatief) wanneer hogere waarden voor de ene variabele samengaan met hogere (lagere) waarden voor de andere. Men zegt in dat geval dat er een positieve (negatieve) associatie is. De noemer in de uitdrukking standaardiseert het geheel waardoor, zoals men wiskundig kan aantonen, de correlatie(coëfficiënt) een getal is gelegen tussen -1 en 1. Uitkomsten die perfect lineair afhankelijk zijn van elkaar (d.w.z. dat ze in een scatterplot gelegen zijn op een rechte lijn) hebben een correlatie van 1 of -1. Onafhankelijke variabelen (d.w.z. variabelen waarvoor kennis van de waarde voor de ene variabele geen informatie levert over de waarde voor de andere variabele) hebben een correlatie gelijk aan 0.

De correlatie tussen de log2-S100A8 en log2-ESR1 expressie bedraagt -0.89. Wat opnieuw op een sterke negatieve correlatie wijst tussen de log-expressie van beide genen.

par(mfrow=c(2,3))
for ( i in c(.3,.7,.99,-.3,-.5,-.9))
  plot(rmvnorm(100,sigma=matrix(c(1,i,i,1),ncol=2)),xlab="x",ylab="y",main=paste("correlatie",i))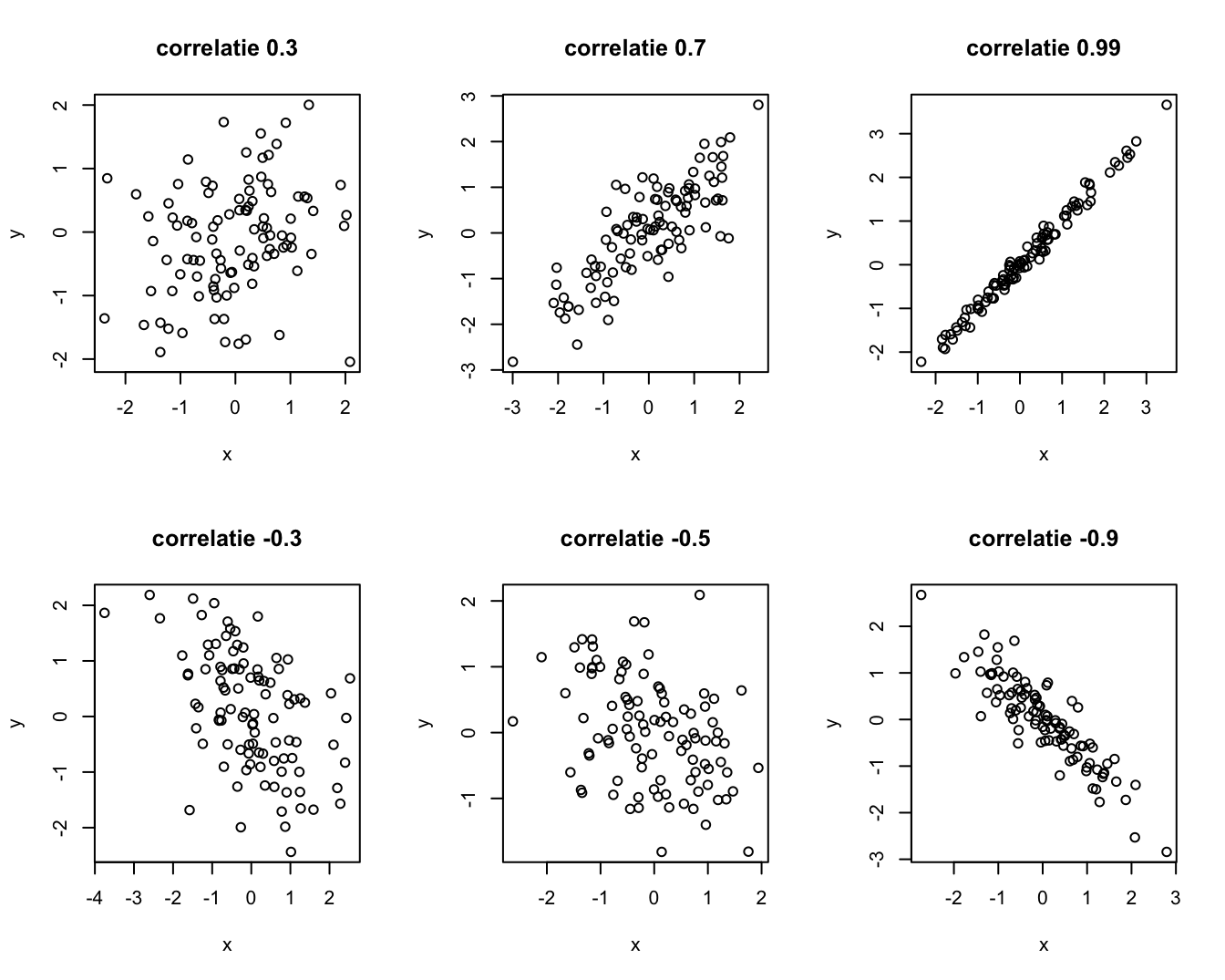

Figuur 4.16: Gesimuleerde gegevens met verschillende correlatie.

Figuur 4.16 toont ter illustratie verschillende scatterplots waar fictieve gegevens met verschillende correlaties werden gesimuleerd. Merk op dat het lineaire patroon tussen de twee reeksen gegevens sterker wordt met toenemende correlatie en van richting wijzigt naarmate de correlatie negatief wordt.

Eigenschap

De correlatie tussen 2 reeksen metingen \((x_i)\) en \((y_i)\) blijft ongewijzigd

wanneer bij alle uitkomsten \(x_i\) een willekeurige constante \(a\) wordt opgeteld;
wanneer alle uitkomsten \(x_i\) met een willekeurige constante \(a\) worden vermenigvuldigd;
wanneer \((x_i,\bar x)\) en \((y_i,\bar y)\) van plaats worden verwisseld in de uitdrukking voor de correlatie.

Einde eigenschap

Op basis van deze eigenschap kunnen we bijvoorbeeld besluiten dat de correlatie tussen de expressie van het S100A8 en ESR1 gen niet gewijzigd wordt wanneer we een log10 transformatie hadden gebruikt ipv een log2 tranformatie. Door de eigenschappen van logaritmes weten we immers dat \(\log_{2}(x)=\log_{10}(x)/\log_{10}(2)\)

set.seed(100)
#Een seed wordt gebruikt om ervoor te zorgen
#dat dezelfde resultaten opnieuw kunnen worden
#bekomen wanneer men at random data genereerd
par(mfrow=c(1,2)) #twee plots naast elkaar
#simuleer
scheef=exp(rmvnorm(100,mean=rep(1.5,2),sigma=matrix(c(1.5,.75*1.5,.75*1.5,1.5),ncol=2)))
#plot
plot(scheef,main=paste("Correlatie",round(cor(scheef)[1,2],2)),xlab="x",ylab="y")
#simuleer
normal <- rmvnorm(100,mean=rep(1.5,2),sigma=matrix(c(1.5,.71*1.5,.71*1.5,1.5),ncol=2))
#plot
plot(normal,main=paste("Correlatie",round(cor(normal)[1,2],2)),xlab="x",ylab="y")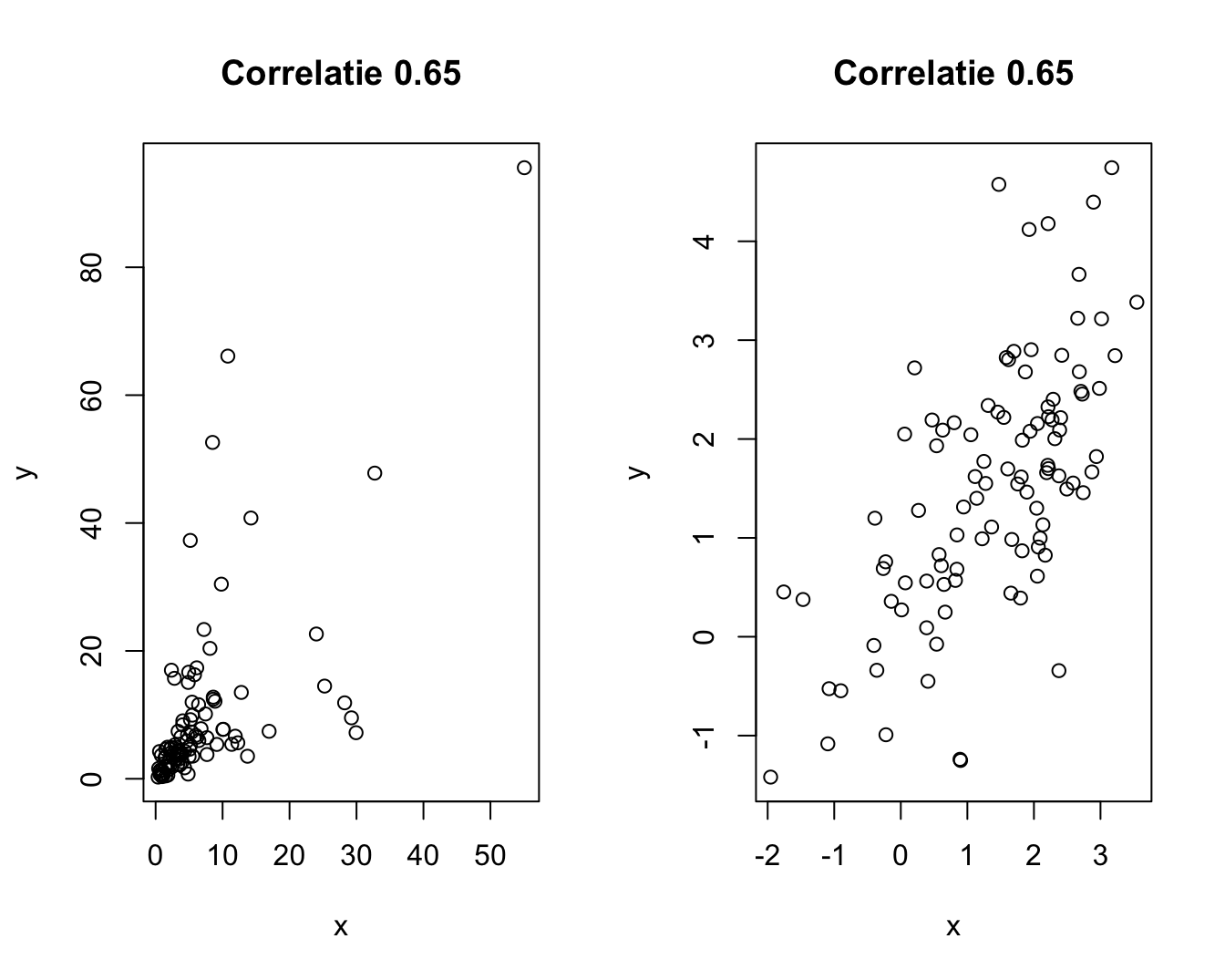

Figuur 4.17: Links: scheef verdeelde observaties; Rechts: Normaal verdeelde observaties.

Bij het interpreteren van correlaties, alsook bij het uitvoeren van regressie-analyses in de volgende secties, zijn de volgende waarschuwingen van zeer groot belang:

Correlaties zijn het makkelijkst te interpreteren tussen 2 groepen Normaal verdeelde observaties. Een kleine training laat immers toe om snel inzicht te krijgen in de grootte van de correlatiecoëfficiënt zonder zich verder over de specifieke verdeling te hoeven bekommeren. In het bijzonder kan men voor Normaal verdeelde observaties visueel inzicht krijgen in de sterkte van de correlatie door een ellips rond de puntenwolk te tekenen die (nagenoeg) alle punten bevat. Als de ellips op een cirkel lijkt, dan is er geen correlatie. Hoe dunner de ellips, hoe sterker de correlatie. De oriëntatie van de ellips geeft hierbij het teken van de correlatie weer.

Voor niet-Normale gegevens hangt de betekenis van een correlatiecoëfficiënt van zekere grootte, nauw samen met de specifieke vorm van de verdeling. Figuur 4.17 toont ter illustratie 1 paar scheef verdeelde (links) en 1 paar Normaal verdeelde (rechts) observaties. Hoewel de correlatie in beide figuren 0.65 bedraagt, tonen beide figuren een verschillende associatie. Merk ook op in Figuur 4.18 (rechts) dat de grootte van de correlatie sterk beïnvloed kan worden door een paar outliers. De correlatie tussen deze variabelen bedraagt slechts 0.44, maar 0.93 na verwijdering van de 2 outliers.

Wanneer de 2 variabelen die we onderzoeken niet Normaal verdeeld zijn, dan zijn er 2 mogelijkheden om een zinvolle correlatiecoëfficiënt weer te geven. Variabelen die scheef verdeeld zijn, kan men transformeren (bvb. een log-transformatie) in de hoop dat de getransformeerde gegevens bij benadering Normaal verdeeld zijn en lineair samenhangen. Bemerk dat we de genexpressie van S100A8 en ESR1 daarom log-getransformeerd hebben in Figuur 4.15, concentraties en intensiteitsmetingen zijn immers vaak log-normaal verdeeld.

Indien transformatie niet helpt of wanneer er outliers zijn, kan men een meer robuuste maat voor de samenhang tussen 2 variabelen rapporteren, zoals de Spearman’s rank correlatie. Dit is per definitie de Pearson correlatiecoëfficiënt van de rangen van de 2 beschouwde variabelen. Dergelijke rangen worden bekomen door voor elke variabele afzonderlijk de metingen te vervangen door de rangorde waarin ze voorkomen. In het bijzonder krijgt de kleinste meting rangorde 1 toegekend, de tweede kleinste rangorde 2, etc. Door aldus rangordes voor de 2 variabelen afzonderlijk te nemen, blijft de samenhang ruwweg behouden, maar wordt de invloed van outliers gevoelig afgezwakt (omdat rangordes relatief gezien nooit extreem worden).

par(mfrow=c(1,2))
set.seed(34)
x=c(rnorm(100))
y=3*x^2+rnorm(100,sd=2)
plot(x,y,main=paste("Correlation",round(cor(x,y),2)))
simHlp=matrix(0,ncol=2,nrow=20)
simHlp[1:18,]=rmvnorm(18,sigma=matrix(c(1,.9,.9,1),ncol=2))
simHlp[19:20,]=cbind(max(simHlp[,1])*c(1.1,1.3),c(-2,-2.8))
plot(simHlp,main=paste("Correlation",round(cor(simHlp)[1,2],2)),xlab="x",ylab="y")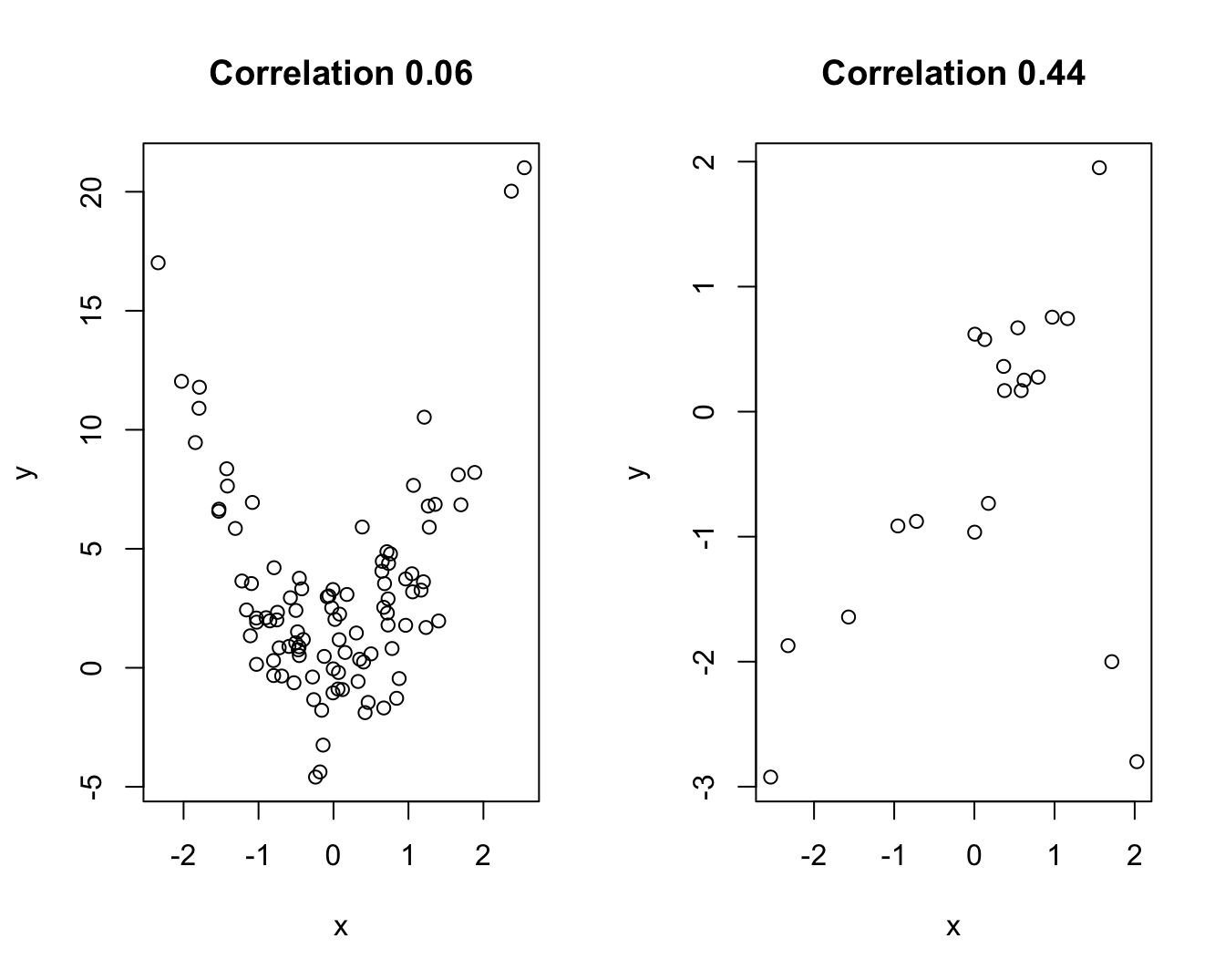

Links: gesimuleerde gegevens met kwadratische associatie; Rechts: gesimuleerde gegevens met een werkelijke correlatie van 0.9 en 2 outliers.

Figuur 4.18: Links: gesimuleerde gegevens met kwadratische associatie; Rechts: gesimuleerde gegevens met een werkelijke correlatie van 0.9 en 2 outliers.

#Met outliers
cor(simHlp)

##           [,1]      [,2]
## [1,] 1.0000000 0.4399447
## [2,] 0.4399447 1.0000000

#Zonder outliers
cor(simHlp[1:18,])

##           [,1]      [,2]
## [1,] 1.0000000 0.9270999
## [2,] 0.9270999 1.0000000

Merk op dat een correlatiecoëfficiënt van 0 tussen 2 variabelen \(X\) en \(Y\) niet noodzakelijk impliceert dat deze variabelen onafhankelijk zijn. Figuur 4.18 (links) toont ter bijvoorbeeld 2 variabelen die vrij sterk geassocieerd zijn, hoewel hun correlatie nagenoeg 0 bedraagt. De oorzaak hiervan is dat de correlatie enkel de lineaire samenhang tussen 2 variabelen meet en bijgevolg niet noodzakelijk niet-lineaire verbanden detecteert. Dit betekent meer concreet dat de correlatie, op een factor na, de helling weergeeft van de `best passende rechte’ (nl. de kleinste kwadratenrechte, zie Hoofdstuk 6) doorheen de puntenwolk. Een correlatie gelijk aan 0 geeft bijgevolg aan dat een best passende rechte doorheen de puntenwolk helling 0 heeft (d.w.z. dat ze horizontaal verloopt). In Figuur 4.18 is de correlatie heel laag omdat er bij negatieve \(X\)-waarden een dalende associatie is en bij positieve \(X\)-waarden een stijgende associatie, zodat de 2 variabelen geen lineaire samenhang meer hebben.

Omwille van het voorgaande fenomeen is het van belang om de aard van samenhang tussen 2 variabelen steeds te onderzoeken via een scatterplot alvorens een correlatiecoëfficiënt te rapporteren. Wanneer het verband monotoon is, maar sterk niet-lineair is, dan is het aangewezen om niet de Pearson correlatiecoëfficiënt, maar Spearman’s correlatiecoëfficiënt te rapporteren.

Figuur 4.19 geeft het verband van de microarray intensiteitsmetingen weer voor het S100A8 gen in functie van deze voor het ESR1 gen. Het verband is moeilijk interpreteerbaar op de originele schaal door de aanwezigheid van heel hoge intensiteiten (en dus concentraties). Het verband op de originele schaal is exponentieel. Pearson’s correlatiecoëfficiënt zakt hierdoor van -0.89 op log-schaal naar -0.54 op de originele schaal. Spearman’s correlatiecoëfficiënt daarentegen blijft gelijk voor en na transformatie gezien de log2 transformatie monotoon is en de ordening (rangen) van de data niet verandert. Spearman’s correlatiecoëfficiënt blijft -0.73 op de originele schaal alsook op log-schaal en wijst op een sterke negatieve associatie tussen de expressie van beiden genen.

par(mfrow=c(1,3))
with(borstkanker, scatter.smooth(log2(ESR1),log2(S100A8),span=1/2,        main=paste("Correlatie",c("Pearson","Spearman"),round(c(cor(log2(ESR1),log2(S100A8)),cor(log2(ESR1),log2(S100A8),method = "spearman")),2))))
with(borstkanker, scatter.smooth(ESR1,S100A8,span=1/2,main=paste("Correlatie",c("Pearson","Spearman"),round(c(cor(ESR1,S100A8),cor(ESR1,S100A8,method = "spearman")),2))))
with(borstkanker, scatter.smooth(ESR1,S100A8,span=1/2,ylim=c(0,500),main=paste("Correlatie",c("Pearson","Spearman"),round(c(cor(ESR1,S100A8),cor(ESR1,S100A8,method = "spearman")),2))))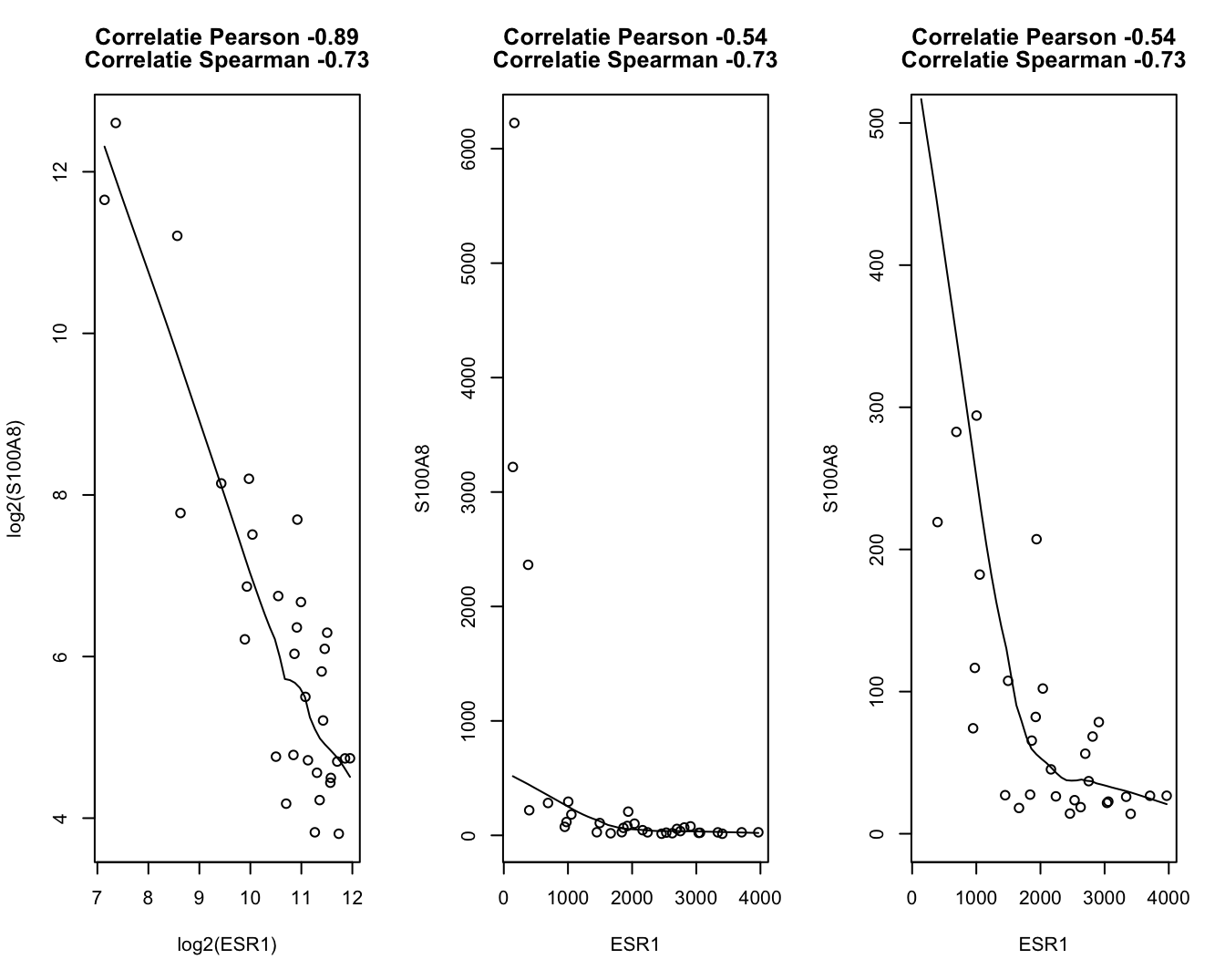

Figuur 4.19: Expressie van het S100A8 gen in functie van de ESR1 gen-expressie op de log2 en originele schaal.

Indien het verband niet-monotoon is, dan zijn correlatiecoëfficiënten niet geschikt en moet men overstappen op meer geavanceerde regressietechnieken.

Bij jonge kinderen is de grootte van hun schoenmaat uiteraard sterk gecorreleerd met hun leescapaciteiten. Dat op zich impliceert echter niet dat het leren van nieuwe woorden hun voeten doet groeien of dat het groeien van hun voeten impliceert dat ze beter kunnen lezen. Ook algemeen²¹ hoeft een correlatie tussen 2 variabelen niet te impliceren dat er een causaal verband is. De relatie tussen 2 metingen kan immers sterk verstoord worden door confounders (bvb. de leeftijd in bovenstaand voorbeeld). Hoewel dit overduidelijk is in bovenstaand voorbeeld, is het in vele andere contexten veel minder duidelijk en worden er, vooral in de populaire literatuur, vaak causale beweringen gemaakt die niet (volledig) door de gegevens worden gestaafd. Volgend voorbeeld illustreert dit.

Voorbeeld 4.6 (Associatie versus causatie)

Wanneer men de incidentie van sterfte ten gevolge van borstkanker uitzet t.o.v. van de vetinname per capita per dag voor een grote steekproef van landen over de ganse wereld, dan stelt men vast dat er sterke positieve correlatie is. Deze correlatie wordt vaak gebruikt om aan te geven dat vetinname leidt tot borstkanker (analoog voor darmkanker). Het bewijs hiervoor is echter zeer zwak. Immers, landen met een grote vetinname hebben ook een hoge inname van suiker. Een grafiek van de incidentie van sterfte ten gevolge van borstkanker t.o.v. van de suikerinname per capita per dag toont een vrijwel even sterke correlatie, hoewel nagenoeg niemand beweert dat suiker borstkanker veroorzaakt. Bovendien zijn vet en suiker op wereldschaal relatief dure producten. Landen met hoge vetinname zijn bijgevolg voornamelijk industrielanden die in heel wat meer verschillen van de andere landen dan alleen hun vetinname… Recente studies (Holmes et al., 1999) hebben intussen sterke indicaties geleverd dat hoog vetverbruik vermoedelijk niet tot borstkanker leidt.

**Einde voorbeeld**

Een ecologische analyse is een statistische analyse waarbij men associaties bestudeert tussen samenvattingsmaten (zoals gemiddelden, incidenties, …) die reeds berekend werden voor groepen subjecten. Dit is het geval in voorgaand voorbeeld waar de associatie wordt onderzocht tussen de incidentie van sterfte t.g.v. borstkanker en de (gemiddelde) dagelijkse vetinname per capita in verschillende landen. Wanneer men aldus een ecologische correlatie vaststelt voor groepen subjecten of individuen (in dit geval, landen), impliceert dat niet noodzakelijk dat deze correlatie ook voor de subjecten zelf opgaat²². Volgend voorbeeld illustreert dit.

Voorbeeld 4.7 (Ecological fallacy)

Voor de 48 staten in de V.S. werden telkens 2 getallen berekend: het percentage van de mensen die in een ander land geboren zijn en het percentage geletterden. De correlatie ertussen bedraagt 0.53 (Robinson, 1950). Dit is een ecologische correlatie omdat de eenheid van de analyse de groep residenten uit een zelfde staat is, en niet de individuele residenten zelf. Deze ecologische correlatie suggereert dat mensen van vreemde afkomst doorgaans beter geschoold zijn (in Amerikaans Engels) dan de oorspronkelijke inwoners. Wanneer men echter de correlatie berekent op basis van de gegevens voor alle individuele residenten, bekomt men -0.11. De ecologische analyse is hier duidelijk misleidend: het teken van de correlatie is er positief omdat mensen van vreemde origine de neiging hebben om te gaan wonen in staten waar de oorspronkelijke bevolking relatief goed geschoold is.

**Einde voorbeeld**

4.7 Onvolledige gegevens

Het gebeurt vaak in de biowetenschappen dat, ondanks zorgvuldig veld- en laboratoriumwerk, metingen die men plande te verzamelen, niet bekomen werden. Men noemt deze dan ontbrekende gegevens of missing data (points).

Minder drastisch, kunnen observaties soms slechts ten dele gekend zijn. Bijvoorbeeld bij een studie van de overlevingsduur van dieren en planten wacht men niet steeds tot alle subjecten gestorven zijn. Op het eind van de studie zal men bijvoorbeeld voor een 50-jarige olifant die in leven is, slechts weten dat de overlevingstijd minstens 50 jaar bedraagt, maar niet de exacte waarde kennen. Zo’n gegeven wordt rechts-gecensureerd genoemd: we weten dat de gewenste observatie rechts van 50 ligt, maar verder niets meer.

Analoog kunnen observaties links-gecensureerd zijn. Bij het meten van bepaalde concentraties kan een detectielimiet bestaan: een ondergrens beneden dewelke het meettoestel geen aanwezigheid kan detecteren. Men weet in zo’n geval dat de concentratie kleiner dan die ondergrens is, maar niet hoeveel kleiner.

Tenslotte vermelden we nog interval-gecensureerde gegevens. Bij het screenen naar HIV bijvoorbeeld, zal men weten dat een subject seropositief geworden is ergens tussen de laatste negatieve HIV test en de eerste positieve HIV test, maar het exacte tijdstip van seroconversie blijft onbekend.

De aanwezigheid van gegevens die niet of slechts partieel zijn opgemeten zorgt altijd voor extra moeilijkheden bij de analyse en interpretatie van de onderzoeksresultaten. Dat is omdat de missende gegevens mogelijks afkomstig zijn van een speciale populatie. Dat is het meest duidelijk in klinische experimenten bij mensen. Patiënten zullen hier vaak de studie verlaten wanneer ze genezen zijn, in welk geval men de metingen van deze patiënten niet te zien krijgt. Dit negeren door enkel de aanwezige gegevens te analyseren, zal de resultaten er slechter doen uitzien dan ze in werkelijkheid zijn. Meestal houdt dat immers de veronderstelling in dat de aanwezige gegevens representatief blijven voor de populatie die men wenst te bestuderen. Dit kan in sommige gevallen de resultaten sterk vertekenen. In de statistische literatuur zijn de laatste jaren heel wat complexe technieken ontwikkeld om hiervoor te corrigeren. Deze technieken worden meer en meer in de statistische software ingebouwd en recent heeft ook R verschillende bibliotheken toegevoegd. Het is echter aangewezen om voor het gebruik van deze gevorderde technieken een statisticus te consulteren.

Zie Sectie 4.4.2.↩
Later zullen we zien dat het nog iets correcter is om te stellen dat 95% van de waarnemingen liggen tussen \(\bar{x} - 1.96 s_x\) en \(\bar{x} + 1.96 s_x\).↩
Hierbij maken we gebruik van het feit dat voor een Normaal verdeelde observatie \(X\), \(P(X=a)=0\) voor elk reëel getal \(a\), zodat \(P(X\leq a)=P(X<a)\).↩
Let wel op want in verschillende boeken krijgt het symbool \(z_{\alpha}\) verschillende definities!↩
Dit interval bevat niet exact \((1-\alpha)100\%\) van de observaties, maar slechts bij benadering, omdat het geen rekening houdt met het feit dat \(\bar x\) en \(\sigma_x\) impreciese schattingen zijn voor \(\mu\) en \(\sigma\) op basis van een eindige steekproef. Meer accurate referentie-intervallen die deze imprecisie in rekening brengen, ook predictie-intervallen genoemd↩
Merk op dat dit design niet optimaal is omdat replicaties op de verkeerde schaal werden bekomen. Idealiter moesten meer dan 2 stukken grond in de studie opgenomen worden omdat de 2 gekozen stukken grond in veel meer kunnen verschillen dan alleen het bodemtype. Verschillen in de verdeling van houtluizen kunnen bijgevolg niet zomaar aan het bodemtype kunnen toegeschreven worden.↩
Al is het nog de vraag of die associatie toevallig is, dan wel systematisch. We komen in het hoofdstuk 9. terug op technieken om dit te onderzoeken.↩
Dit is bijvoorbeeld het geval in logistische regressiemodellen die gebruikt worden om het risico op een bepaalde aandoening te modelleren in functie van prognostische factoren.↩
In het Engels is dit welbekend onder de zinsnede `Association is not causation!’.↩
In het Engels is dit welbekend onder de naam `ecological fallacy’.↩