Hoofdstuk 11 Modelselectie
11.1 Inleiding
In de prostaatkanker dataset (Sectie 10.1.1) zijn veel predictoren aanwezig. Automatische selectieprocedures kunnen behulpzaam zijn als het doel van het regressiemodel erin bestaat om (1) de uitkomst op basis van de predictoren te voorspellen; of (2) associaties tussen de uitkomst en predictoren te beschrijven. Net zoals in vele andere aspecten van de statistiek, zullen we een geobserveerde dataset (steekproef) gebruiken om tot een resultaat te komen (hier: een model) dat ruimer toepasbaar is dan enkel op de geobserveerde data. Het geselecteerde model moet toepasbaar zijn op de ruimere populatie waaruit de steekproefdata bekomen is en waarop de onderzoeksvraag van toepassing is.
Modelselectie kan dan omschreven worden als een methode voor het selecteren van een model dat best geschikt is voor het beantwoorden van de onderzoeksvraag. In dit hoofdstuk beperken we ons tot meervoudige lineaire regressiemodellen waarin sommige van de \(p-1\) effecttermen mogelijks interactietermen voorstellen. Het totaal aantal mogelijke modellen is dan (zonder hiërarchie-restrictie) \(2^{p-1}\) (ieder van de \(p-1\) termen kan opgenomen worden in het model, of niet).
We onderscheiden de volgende algemene procedures:
Alle mogelijke modellen worden geëvalueerd. Deze methode zal enkel haalbaar blijken als het aantal kandidaat modellen niet te groot is.
Niet alle modellen worden geëvalueerd (stapsgewijze procedures): De methode wordt geïnitialiseerd met een model. D.m.v. een regel en een evaluatiecriterium wordt het pad doorheen de modelruimte bepaald.
Merk op dat we hiërarchisch moeten modelleren als we interactietermen toelaten. Een interactieterm mag nooit in het model voorkomen zonder de lagere orde termen.
11.2 Modelselectie op basis van hypothesetesten
Stel, we willen een model selecteren voor lpsa waarbij lcavol, lweight en svi als predicoren worden toegelaten, alsook alle paarsgewijze interactietermen. We zullen drie verschillende strategiën beschouwen voorwaartse modelselectie, achterwaartse modelselecties en stapsgewijze modelselectie waarbij er in elke stap geëvalueerd wordt of een term in het model kan worden opgenomen en of er een andere term kan worden verwijderd.
11.2.1 Voorwaartse modelselectie
De procedure kan als volgt beschreven worden:
- Start met het minimale model \(m_1\) met enkel het intercept
- Test voor alle modellen met slechts 1 predictor (er zijn dus \(p-1\) dergelijke modellen) of de toegevoegde regressor significant verschillend is van 0 op het \(\alpha_{\text{IN}}\) significantieniveau.
- Indien geen enkele van de \(p\)-waarden kleiner is dan \(\alpha_{\text{IN}}\), stop de procedure. Het finale model is het minimale model \(m_1\), \[ Y_i = \beta_0 + \epsilon_i \] met \(\epsilon_i \text{ i.i.d. } N(0,\sigma^2)\).
- Indien er minstens 1 \(p\)-waarde kleiner is dan \(\alpha_{\text{IN}}\), selecteer het model dat overeenkomt met de kleinste \(p\)-waarde. Dit model wordt \(m_2\) genoemd.
- Stel \(k=2\).
- Definieer de verzameling van modellen met 1 predictor toegevoegd aan \(m_{k}\). Test dat de parameter van de toegevoegde regressor significant verschillend is van 0 op het \(\alpha_{\text{IN}}\) significantieniveau.
- Indien geen enkel van de \(p\)-waarden kleiner is dan \(\alpha_{\text{IN}}\), stop de procedure. Het finale model is \[ Y_i = \beta_0 + \sum_{j \in m_k} \beta_j x_{ij} + \epsilon_i \] met \(\epsilon_i \text{ i.i.d. } N(0,\sigma^2)\).
- Indien er minstens één \(p\)-waarde kleiner is dan \(\alpha_{\text{IN}}\), selecteer het model dat overeenkomt met de kleinste \(p\)-waarde. Dit model wordt \(m_{k+1}\) genoemd.
- Verhoog \(k\) met 1 (i.e. \(k\leftarrow k+1\)) en ga naar stap 6.
Voorbeeld voor lpsa. We laten interactietermen toe, maar de modelbouw moet zich houden aan de hiërarchie van hoofd- en interactietermen. We stellen \(\alpha_{\text{IN}}=5\%\).
m1 <- lm(lpsa ~ 1, data=prostate)
add1(m1,scope=~lweight+lcavol+svi+lweight:lcavol+lweight:svi +lcavol:svi,test="F")## Single term additions
##
## Model:
## lpsa ~ 1
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 127.918 28.838
## lweight 1 16.041 111.877 17.841 13.621 0.000373 ***
## lcavol 1 69.003 58.915 -44.366 111.267 < 2.2e-16 ***
## svi 1 41.011 86.907 -6.658 44.830 1.499e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1m2 <- update(m1,~. + lcavol)
add1(m2,scope=~lweight+lcavol+svi+lweight:lcavol+lweight:svi +lcavol:svi,test="F")## Single term additions
##
## Model:
## lpsa ~ lcavol
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 58.915 -44.366
## lweight 1 5.9484 52.966 -52.690 10.5567 0.001606 **
## svi 1 5.2375 53.677 -51.397 9.1719 0.003172 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1m3 <- update(m2,~ . + lweight)
add1(m3,scope=~lweight+lcavol+svi+lweight:lcavol+lweight:svi +lcavol:svi,test="F")## Single term additions
##
## Model:
## lpsa ~ lcavol + lweight
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 52.966 -52.690
## svi 1 5.1814 47.785 -60.676 10.084 0.002029 **
## lweight:lcavol 1 0.1222 52.844 -50.914 0.215 0.643962
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1m4 <- update(m3,~ . + svi)
add1(m4,scope=~lweight+lcavol+svi+lweight:lcavol+lweight:svi +lcavol:svi,test="F")## Single term additions
##
## Model:
## lpsa ~ lcavol + lweight + svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 47.785 -60.676
## lweight:lcavol 1 0.36606 47.419 -59.422 0.7102 0.4016
## lweight:svi 1 1.16445 46.621 -61.069 2.2979 0.1330
## lcavol:svi 1 0.02433 47.761 -58.725 0.0469 0.8291summary(m4)##
## Call:
## lm(formula = lpsa ~ lcavol + lweight + svi, data = prostate)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.72966 -0.45767 0.02814 0.46404 1.57012
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.26807 0.54350 -0.493 0.62301
## lcavol 0.55164 0.07467 7.388 6.3e-11 ***
## lweight 0.50854 0.15017 3.386 0.00104 **
## sviinvasion 0.66616 0.20978 3.176 0.00203 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7168 on 93 degrees of freedom
## Multiple R-squared: 0.6264, Adjusted R-squared: 0.6144
## F-statistic: 51.99 on 3 and 93 DF, p-value: < 2.2e-16Het geselecteerde model is \[ Y_i = \beta_0 + \beta_v X_{iv} + \beta_w X_{iw} + \beta_s X_{is} + \epsilon_i \] met \(\epsilon_i \text{ i.i.d. } N(0,\sigma^2)\).
11.2.2 Achterwaartse modelselectie
Achterwaartse modelselectie is een procedure die ook gekend staat als achterwaartse eliminatie (Engels: backward elimination).
De procedure start van het maximale model en gaat na welke predictoren uit het model kunnen worden verwijderd.
- Start met het maximale model \(m_1\) met alle \(p-1\) regressoren
- Bouw alle modellen waar 1 predictor wordt weggelaten en ga via een F-test na of het verwijderen van de predictoren significant is op het \(\alpha_{\text{OUT}}\) significantieniveau. Merk op dat deze test in model \(m_1\) moet uitgevoerd worden.
- Indien geen enkele van de \(p\)-waarden groter is dan \(\alpha_{\text{OUT}}\), stop de procedure. Het finale model is het maximale model \(m_1\).
- Indien er minstens één \(p\)-waarde groter dan \(\alpha_{\text{OUT}}\) is, selecteer het model dat overeenkomt met de grootste \(p\)-waarde. Dit model wordt \(m_2\) genoemd.
- Stel \(k=2\)
- Bouw alle modellen waar 1 predictor wordt weggelaten uit \(m_k\) en ga via een F-test na of het verwijderen van de predictoren significant is op het \(\alpha_{\text{OUT}}\) significantieniveau. Merk op dat deze test in model \(m_k\) moet uitgevoerd worden.
- Indien geen enkel van de \(p\)-waarden groter is dan \(\alpha_{\text{OUT}}\), stop de procedure. Het finale model is \(m_k\)
- Indien er minstens één \(p\)-waarde groter is dan \(\alpha_{\text{OUT}}\), selecteer het model dat overeenkomt met de grootste \(p\)-waarde. Dit model wordt \(m_{k+1}\) genoemd.
- Verhoog \(k\) met één (i.e. \(k\leftarrow k+1\)) en ga naar stap 6.
We passen de achterwaartse modelselectie toe op het prostaatkanker voorbeeld. We zoeken naar een model met enkel de belangrijke termen (i.e. significante termen) die geassocieerd zijn met lpsa. We laten interactietermen toe, maar de modelbouw moet zich houden aan de hiërarchie van hoofd- en interactietermen. We stellen \(\alpha_{\text{OUT}}=5\%\).
alphaOut <- 0.05
m<- lm(lpsa~lweight+lcavol+svi+lweight:lcavol+lweight:svi +lcavol:svi,prostate)
dropHlp<-drop1(m,test="F")
dropHlp## Single term deletions
##
## Model:
## lpsa ~ lweight + lcavol + svi + lweight:lcavol + lweight:svi +
## lcavol:svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 46.478 -57.365
## lweight:lcavol 1 0.00012 46.479 -59.365 0.0002 0.9878
## lweight:svi 1 0.87404 47.353 -57.558 1.6925 0.1966
## lcavol:svi 1 0.14093 46.619 -59.071 0.2729 0.6027Merk op dat eerst enkel de interactietermen worden getest. De hoofdeffecten mogen niet uit het model worden weggelaten zolang er interactie termen in het model zijn opgenomen waarin deze hoofdeffecten voorkomen.
while (sum(dropHlp[,6]>=alphaOut,na.rm=TRUE))
{
dropVarName<-rownames(dropHlp)[which.max(dropHlp[,6])]
m <- update(m,as.formula(paste("~.-",dropVarName)))
dropHlp<-drop1(m,test="F")
print(dropHlp)
}## Single term deletions
##
## Model:
## lpsa ~ lweight + lcavol + svi + lweight:svi + lcavol:svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 46.479 -59.365
## lweight:svi 1 1.2820 47.761 -58.725 2.5100 0.1166
## lcavol:svi 1 0.1419 46.621 -61.069 0.2778 0.5994
## Single term deletions
##
## Model:
## lpsa ~ lweight + lcavol + svi + lweight:svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 46.621 -61.069
## lcavol 1 28.1995 74.820 -17.184 55.6484 4.711e-11 ***
## lweight:svi 1 1.1644 47.785 -60.676 2.2979 0.133
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Single term deletions
##
## Model:
## lpsa ~ lweight + lcavol + svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 47.785 -60.676
## lweight 1 5.8923 53.677 -51.397 11.468 0.001039 **
## lcavol 1 28.0446 75.830 -17.884 54.581 6.304e-11 ***
## svi 1 5.1814 52.966 -52.690 10.084 0.002029 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Merk op dat opnieuw hetzelfde model wordt gekozen. Dat is in het algemeen niet het geval. Vaak heeft achterwaartse modelselectie de eigenschap om te resulteren in een meer complex model dan voorwaartse selectie.
11.2.3 Stapsgewijze modelselectie
Deze methode is een combinatie van voorwaartse en achterwaartse modelselectie. Het kan starten van het maximale of het minimale model. We implementeren de methode, startende van het minimale model. In elke stap zal eerst worden gekeken of een predictor kan worden toegevoegd, vervolgens zal worden nagegaan of een predictor kan worden verwijderd van het model.
alphaIn <- alphaOut <- 0.05
m <- lm(lpsa ~ 1 ,prostate)
notConverged <- TRUE
while (notConverged)
{
addHlp <- add1(m,scope= ~lweight+lcavol+svi+lweight:lcavol+lweight:svi +lcavol:svi,test="F")
print(addHlp)
addVarName<-rownames(addHlp)[which.min(addHlp[,6])]
if ((sum(addHlp[,6] < alphaIn,na.rm=TRUE))>0) m <- update(m,as.formula(paste("~.+",addVarName)))
dropHlp<-drop1(m,test="F")
print(dropHlp)
if ((sum(dropHlp[,6]>=alphaOut,na.rm=TRUE))>0) m <- update(m,as.formula(paste("~.-",dropVarName)))
if ((sum(addHlp[,6] < alphaIn,na.rm=TRUE) + sum(dropHlp[,6]>=alphaOut,na.rm=TRUE))>0) notConverged <- TRUE else notConverged <- FALSE
}## Single term additions
##
## Model:
## lpsa ~ 1
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 127.918 28.838
## lweight 1 16.041 111.877 17.841 13.621 0.000373 ***
## lcavol 1 69.003 58.915 -44.366 111.267 < 2.2e-16 ***
## svi 1 41.011 86.907 -6.658 44.830 1.499e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Single term deletions
##
## Model:
## lpsa ~ lcavol
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 58.915 -44.366
## lcavol 1 69.003 127.918 28.838 111.27 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Single term additions
##
## Model:
## lpsa ~ lcavol
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 58.915 -44.366
## lweight 1 5.9484 52.966 -52.690 10.5567 0.001606 **
## svi 1 5.2375 53.677 -51.397 9.1719 0.003172 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Single term deletions
##
## Model:
## lpsa ~ lcavol + lweight
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 52.966 -52.690
## lcavol 1 58.910 111.877 17.841 104.549 < 2.2e-16 ***
## lweight 1 5.948 58.915 -44.366 10.557 0.001606 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Single term additions
##
## Model:
## lpsa ~ lcavol + lweight
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 52.966 -52.690
## svi 1 5.1814 47.785 -60.676 10.084 0.002029 **
## lweight:lcavol 1 0.1222 52.844 -50.914 0.215 0.643962
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Single term deletions
##
## Model:
## lpsa ~ lcavol + lweight + svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 47.785 -60.676
## lcavol 1 28.0446 75.830 -17.884 54.581 6.304e-11 ***
## lweight 1 5.8923 53.677 -51.397 11.468 0.001039 **
## svi 1 5.1814 52.966 -52.690 10.084 0.002029 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Single term additions
##
## Model:
## lpsa ~ lcavol + lweight + svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 47.785 -60.676
## lweight:lcavol 1 0.36606 47.419 -59.422 0.7102 0.4016
## lweight:svi 1 1.16445 46.621 -61.069 2.2979 0.1330
## lcavol:svi 1 0.02433 47.761 -58.725 0.0469 0.8291
## Single term deletions
##
## Model:
## lpsa ~ lcavol + lweight + svi
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 47.785 -60.676
## lcavol 1 28.0446 75.830 -17.884 54.581 6.304e-11 ***
## lweight 1 5.8923 53.677 -51.397 11.468 0.001039 **
## svi 1 5.1814 52.966 -52.690 10.084 0.002029 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Merk op dat er voor dit voorbeeld nooit een predictor uit het model werd verwijderd eens die werd opgenomen in het model. Dat is in het algemeen niet het geval.
11.2.4 Opmerkingen
Eerst een opmerking over de toepassing van de drie modelselectiemethoden op het prostaat voorbeeld. De drie methoden resulteerden in hetzelfde finale geselecteerde model (met enkel hoofdeffecten van lcavol, lweight en svi). In het algemeen leiden de drie methoden niet noodzakelijk tot eenzelfde finale model.
De \(p\)-waarden in het geselecteerde model mogen niet geïnterpreteerd worden. Dit is minder eenvoudig om in te zien. We hebben immers meerdere hypothese testen uitgevoerd om tot dit model te komen. Bovendien zorgt de modelselectie ervoor dat enkel “significante” termen in het finale model staan; de selectieprocedure is dus een doelbewuste aanrijkingsprocedure. Herinner je dat de definitie van de \(p\)-waarde de kans onder \(H_0\) is dat de teststatistiek “door zuiver toeval” minstens zo extreem is dan deze die waargenomen werd. Door de aanrijking via de modelselectieprocedure, is het niet langer “zuiver toeval” dat de teststatistiek groter is dan de geobserveerde.
Er is geen theoretische basis voor de selectieprocedure. Intuïtief lijkt de procedure zinvol omdat we gewend zijn om beslissingen te nemen aan de hand van hypothesetesten, maar hypothesetesten zijn eigenlijk enkel geldig wanneer ze doelgericht toegepast worden om een vooraf (i.e. voor het observeren van de data) duidelijk omschreven onderzoeksvraag te beantwoorden. Bij modelselectie wordt het pad doorheen de modellenruimte bepaald door de geobserveerde data, waardoor de \(p\)-waarden hun betekenis verliezen, i.e. de hypotheses worden niet vooraf door de onderzoekers geformuleerd, maar ze worden door de data bepaald.
De analyse van lpsa in het vorige hoofdstuk zou ook als modelselectie kunnen worden bekeken: we startten met het model met de hoofdeffecten en met interactietermen. Vervolgens werd getest of de interactieterm nul was. Indien de interactieterm niet significant was, dan werd deze verwijderd en werden de hoofdeffecten getest. Dit lijkt op een achterwaartse modelselectie, maar in dat voorbeeld moeten we de procedure interpreteren als een klassieke hypothesetest (voor interactie) waarvan de nulhypothese in de onderzoeksvraag verscholen lag en dus niet door de data gesuggereerd werd.
11.3 Modelselectie voor predictie
11.3.1 Inleiding
In het vroege stadium van de ontwikkeling van een nieuw geneesmiddel (Engels: early drug development) kijkt men tegenwoordig ook naar het effect van de werkzame stof (compound) op genexpressie. Dit kan een dieper inzicht geven in de werking van het geneesmiddel, of kan toxiciteit van de compound in een vroeg stadium detecteren (toxicogenomics). De gewenste activiteit van een compound wordt in vitro bepaald aan de hand van bio-assays (BA). De uitkomst is bv. een maat voor de bindingscapaciteiten van de compound aan de geviseerde receptor op de celwand (IC\(_{50}\)). Deze receptor wordt de target genoemd.
In deze vroege fase van de ontwikkeling van een geneesmiddel worden typisch 20 tot 50 gelijkaardige compounds uitvoerig getest. Op basis van de in vitro resultaten nemen de chemici beslissingen over hoe de molecules moeten aangepast worden om tot een (hopelijk) betere compound te komen (i.e. een hogere on-target activiteit en minder toxiciteit).
De kleine variaties in moleculaire structuur geven aanleiding tot variaties in BA en genexpressies.
De doelstelling van de studie is het opstellen van een model dat toelaat de bioactiviteit (BA) te voorspellen aan de hand van genexpressies in een levercellijn.
In het volgend voorbeeld, wordt het effect van 35 compounds getest op de genexpressie van levercellen. De levercellen werden gedurende 24 uur blootgesteld aan de compound, waarna genexpressie gemeten werd m.b.v. microarrays. De on-target bioactiviteit van ieder van de 35 compounds wordt via een in-vitro bioassay bekomen (IC\(_{50}\)).
We beperken ons hier tot 10 genen (geselecteerd door het onderzoeksteam op basis van a-priori kennis van de pathways betrokken bij de ontwikkeling van de ziekte). Figuur 11.1 toont de scatter plot matrix.
mcx<-read.table("dataset/mcx.txt",header=TRUE)
head(mcx)## BA HOXB5 PNISR ATRX LOC100505650 PLK1S1 DNAJC12 ZFHX4
## 1 5.70 9.864744 9.421823 8.557665 11.08555 8.892243 8.198292 8.846125
## 2 5.87 9.847176 9.301424 8.550591 11.18236 9.196701 8.343191 8.873578
## 3 5.70 9.859438 9.360302 8.536606 11.03822 8.903690 8.231318 8.859549
## 4 5.54 9.862448 9.283498 8.535854 10.98804 9.136609 8.292451 8.857473
## 5 5.32 9.836761 9.309442 8.543522 10.94489 8.855404 8.197822 8.826820
## 6 5.73 9.848315 9.318502 8.545635 11.01789 8.919469 8.272741 8.838364
## BSDC1 FTSJ1 YPEL1
## 1 8.848922 10.38470 8.265589
## 2 9.022556 10.23077 8.426856
## 3 8.888275 10.37585 8.244617
## 4 8.985628 10.35854 8.257426
## 5 8.832436 10.37179 8.250075
## 6 8.864538 10.38892 8.280436plot(mcx)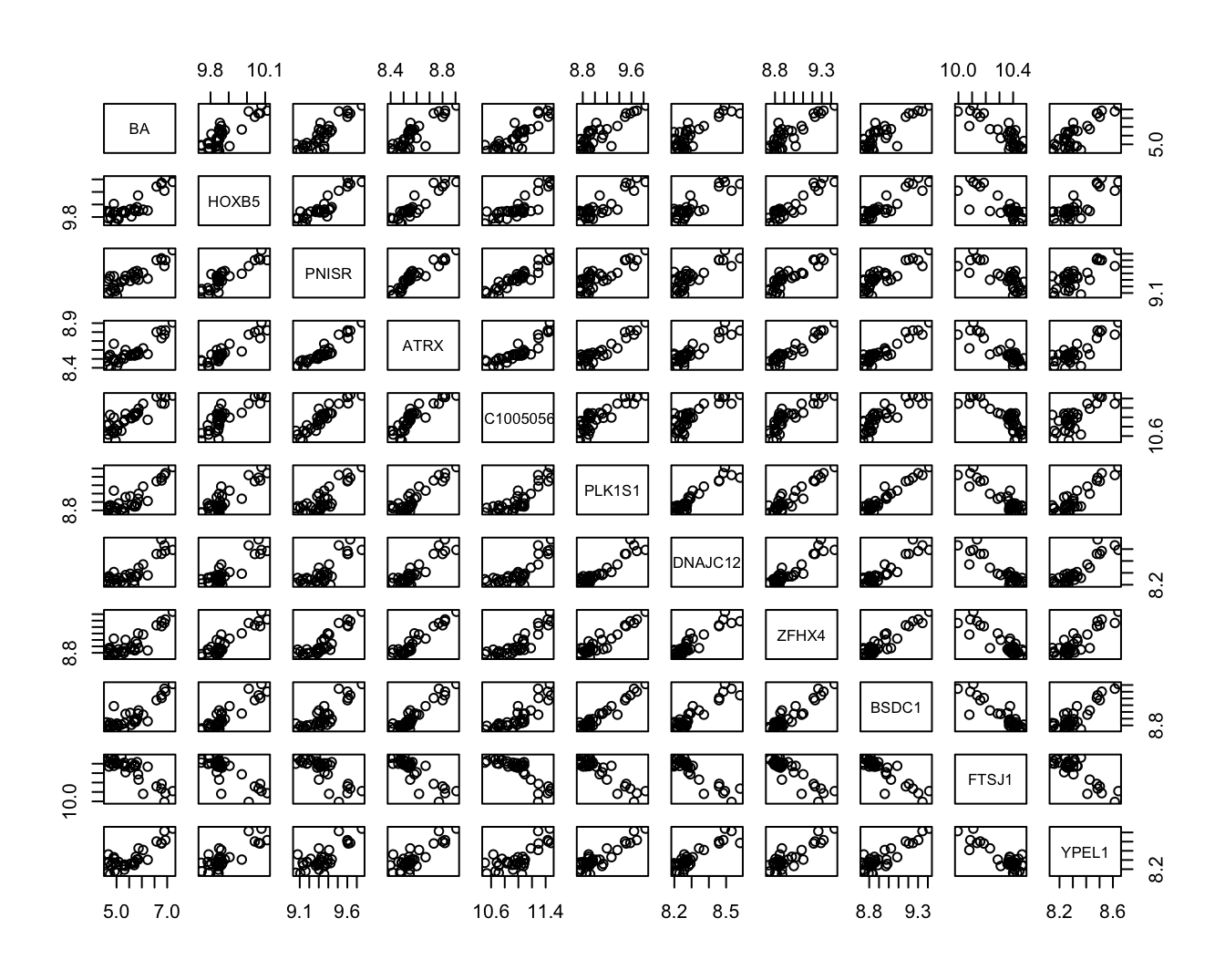
Figuur 11.1: Scatterplot matrix voor de observaties in de bioactiviteit dataset.
Figuur 11.1 suggereert dat de BA uitkomst sterk gecorreleerd is met alle genexpressies, maar de figuur toont tevens dat vele genexpressies ook onderling sterk gecorreleerd zijn. Het zal dus waarschijnlijk niet nodig zijn om alle genen simultaan in het model op te nemen. Niettegenstaande de hypothesetest-gebaseerde methoden toepasbaar lijken, argumenteren we hier dat die methoden niet geschikt zijn in de huidige context.
De doelstelling is om een zo optimaal mogelijk model te selecteren dat gebruikt kan worden voor predictie van de uitkomst. Niettegenstaande de predictie voor een lineair regressiemodel gegeven wordt door \(\hat{Y}=\beta_0+\sum_{j=1}^{p-1}\beta_jX_j\), weten we dat de \(\beta\)-parameters een interpretatie hebben met betrekking tot de gemiddelde uitkomst \(\text{E}[Y\mid (X_1,\ldots,X_{p-1})]=\beta_0+\sum_{j=1}^{p-1}\beta_jX_j\). Hypothesetesten voor \(H_0:\beta_j=0\) gaan dus na of predictor \(X_j\) (conditioneel op de andere regressoren in het model) gerelateerd is tot de gemiddelde uitkomst. Het al dan niet verwerpen van \(H_0\) heeft niet enkel te maken met de werkelijke waarde van \(\beta_j\), maar ook met de kracht van de hypothesetest en dus ook met de steekproefgrootte \(n\). Hypothesetesten maken een afweging van de evidentie in de data tegen/voor de gestelde hypotheses die betrekking hebben op de gemiddelde uitkomst. Voor een goed predictiemodel is het minder belangrijk dat het model de werkelijkheid weerspiegelt met betrekking tot het verband tussen de gemiddelde uitkomst en de regressoren; het is enkel belangrijk dat het model goede predicties geeft voor individuele uitkomsten. Om deze reden wordt modelselectie voor predictiemodellen uitgevoerd door gebruik te maken van specifieke modelselectiecriteria die de kwaliteit van het predictieve karakter van een model kwantificeert.
11.3.2 Selectie-criterium
Het is aanlokkelijk om \(R^2\) te gebruiken als een criterium voor hoe goed het model in staat is om predicties te maken, gezien het aangeeft hoeveel procent van de variabiliteit in de data verklaard kan worden door het model. \(R^2\) is echter geen goed criterium. Hoe complexer het model (hoe meer predictoren er worden opgenomen) hoe hoger \(R^2\) wordt. \(R^2 = 1-SSE/SSTot = SSR/SSTot\) en SSE (SSR) neemt immers steeds af(toe) als een extra predictor in het model wordt opgenomen terwijl SSTot constant blijft. Het gebruik van \(R^2\) zal dus aanleiding geven tot overfitting. We zullen immers steeds het meest complexe model selecteren. Hierdoor zal het model niet meer goed veralgemenen naar nieuwe data toe: het model wordt als het ware te goed getuned naar de dataset die is gebruikt om het model te trainen waardoor het niet meer bruikbaar is om predicties te doen.
Het Akaike Information Criterium (AIC) is een criterium dat een compromis maakt tussen de kwaliteit van de fit en de complexiteit van het model. \[AIC = -2 \text{ln } L(\hat \beta_0, \ldots, \hat \beta_{p-1}, \hat \sigma^2) + 2 (p+1),\]
waarbij de eerste term het natuurlijke logaritme is van likelihood, die voor een steekproef van \(n\) i.i.d. normaal verdeelde observaties met dichtheidsfunctie \(f(Y_i \vert x_{i1} \ldots x_{ip-1}, \beta_0,\ldots, \beta_{p-1} ,\sigma^2)\) en conditioneel gemiddelde \(E[Y_i \vert x_{i1} \ldots x_{ip-1}]=\beta_0 + \sum_{j=1}^{p-1} \beta_j x_{j}\) gedefinieerd is als: \[ L(\beta_0, \ldots, \beta_{p-1}, \sigma^2) = \prod\limits_{i=1}^n f(y_i \ldots x_{ip-1}, \beta_0,\ldots, \beta_{p-1} ,\sigma^2) \]
De likelihood geeft dus weer hoe waarschijnlijk het is om de data te observeren onder het normale regressiemodel. Gezien we de parameters niet kennen zullen we ze vervangen door de geschatte modelparameters. We kunnen voor het Normale lineaire regressie model aantonen dat \(-2 \text{ln } L(\hat \beta_0, \ldots, \hat \beta_{p-1}, \hat \sigma^2)\) evenredig is met SSE. Hoe slechter de fit is, hoe hoger het AIC criterium.
De tweede term straft de kwaliteit van de fit als het ware af voor complexiteit. Merk op dat \(p+1\) het aantal modelparameters is die we schatten met het normale regressie model: \(p\) parameters van het lineaire model + de parameter \(\sigma^2\). Het AIC criterium zal dus ook toenemen i.f.v. de complexiteit van het model (aantal parameters). Hierdoor wordt een afweging gemaakt tussen de kwaliteit van de model fit (term 1) en de complexiteit van het model (term 2).
Merk op dat de data analist het werkelijk model niet kent. Hij/zij zal dus verschillende kandidaat modellen met elkaar vergelijken. Vervolgens wordt het model geselecteerd waaronder het zo waarschijnlijk mogelijk is om de geobserveerde data te trekken in een steekproef (eerste term minimaal, SSE zo laag mogelijk), maar zonder dat de modelcomplexiteit daarbij te hoog wordt (tweede term). De analist zal dus het modelselecteren met een zo klein mogelijke AIC.
Opnieuw kan men gebruik maken van voorwaarts, achterwaartse of stapsgewijze modelselectie. Dat kan eenvoudig in R worden geïmplementeerd a.d.h.v. de ‘step’ functie.
We passen de strategie nu toe op het bioactiviteitsvoorbeeld. We zullen opnieuw voorwaartse, achterwaartse en stapsgewijze modelselectie uitvoeren.
Bij voorwaartse modelselectie starten we van een model zonder predictoren:
m1 <- lm(BA~1,mcx)
m1##
## Call:
## lm(formula = BA ~ 1, data = mcx)
##
## Coefficients:
## (Intercept)
## 5.55mfull <- lm(BA~.,mcx)
mfull##
## Call:
## lm(formula = BA ~ ., data = mcx)
##
## Coefficients:
## (Intercept) HOXB5 PNISR ATRX LOC100505650
## -9.5823 1.1665 2.6174 -2.0386 0.3095
## PLK1S1 DNAJC12 ZFHX4 BSDC1 FTSJ1
## 0.4614 0.4616 -0.7015 -0.2761 -1.6318
## YPEL1
## 1.3044mForward <- step(m1,scope=formula(mfull),direction="forward")## Start: AIC=-19.33
## BA ~ 1
##
## Df Sum of Sq RSS AIC
## + LOC100505650 1 14.668 4.3588 -68.910
## + PNISR 1 14.376 4.6505 -66.643
## + ATRX 1 14.104 4.9231 -64.650
## + ZFHX4 1 13.869 5.1574 -63.022
## + PLK1S1 1 13.860 5.1671 -62.956
## + FTSJ1 1 13.781 5.2459 -62.426
## + BSDC1 1 13.703 5.3234 -61.913
## + DNAJC12 1 13.412 5.6141 -60.052
## + HOXB5 1 13.400 5.6263 -59.976
## + YPEL1 1 13.049 5.9774 -57.858
## <none> 19.0266 -19.333
##
## Step: AIC=-68.91
## BA ~ LOC100505650
##
## Df Sum of Sq RSS AIC
## + YPEL1 1 1.20478 3.1540 -78.233
## + DNAJC12 1 0.91062 3.4482 -75.112
## + PLK1S1 1 0.81030 3.5485 -74.109
## + FTSJ1 1 0.78960 3.5692 -73.905
## + BSDC1 1 0.75759 3.6012 -73.592
## + HOXB5 1 0.69933 3.6595 -73.031
## + ZFHX4 1 0.69895 3.6599 -73.027
## + ATRX 1 0.63276 3.7261 -72.400
## + PNISR 1 0.36333 3.9955 -69.956
## <none> 4.3588 -68.910
##
## Step: AIC=-78.23
## BA ~ LOC100505650 + YPEL1
##
## Df Sum of Sq RSS AIC
## <none> 3.1540 -78.233
## + PNISR 1 0.133032 3.0210 -77.741
## + HOXB5 1 0.116332 3.0377 -77.548
## + FTSJ1 1 0.063065 3.0910 -76.940
## + ATRX 1 0.048977 3.1051 -76.781
## + DNAJC12 1 0.044347 3.1097 -76.729
## + ZFHX4 1 0.029234 3.1248 -76.559
## + BSDC1 1 0.029032 3.1250 -76.557
## + PLK1S1 1 0.025778 3.1283 -76.520Nu achterwaartse modelselectie:
mBackward <- step(mfull,direction="backward")## Start: AIC=-67.34
## BA ~ HOXB5 + PNISR + ATRX + LOC100505650 + PLK1S1 + DNAJC12 +
## ZFHX4 + BSDC1 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - BSDC1 1 0.003369 2.7288 -69.302
## - DNAJC12 1 0.005688 2.7312 -69.272
## - LOC100505650 1 0.014735 2.7402 -69.156
## - PLK1S1 1 0.025044 2.7505 -69.025
## - ZFHX4 1 0.030840 2.7563 -68.951
## - HOXB5 1 0.039762 2.7652 -68.838
## - ATRX 1 0.063271 2.7887 -68.542
## - YPEL1 1 0.139909 2.8654 -67.593
## - FTSJ1 1 0.157697 2.8832 -67.376
## <none> 2.7255 -67.345
## - PNISR 1 0.211967 2.9374 -66.723
##
## Step: AIC=-69.3
## BA ~ HOXB5 + PNISR + ATRX + LOC100505650 + PLK1S1 + DNAJC12 +
## ZFHX4 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - DNAJC12 1 0.006916 2.7357 -71.213
## - LOC100505650 1 0.014255 2.7431 -71.119
## - PLK1S1 1 0.025052 2.7539 -70.982
## - ZFHX4 1 0.028026 2.7569 -70.944
## - HOXB5 1 0.036934 2.7658 -70.831
## - ATRX 1 0.087988 2.8168 -70.191
## - YPEL1 1 0.136972 2.8658 -69.587
## - FTSJ1 1 0.155963 2.8848 -69.356
## <none> 2.7288 -69.302
## - PNISR 1 0.228042 2.9569 -68.492
##
## Step: AIC=-71.21
## BA ~ HOXB5 + PNISR + ATRX + LOC100505650 + PLK1S1 + ZFHX4 + FTSJ1 +
## YPEL1
##
## Df Sum of Sq RSS AIC
## - LOC100505650 1 0.014893 2.7506 -73.023
## - ZFHX4 1 0.025561 2.7613 -72.887
## - PLK1S1 1 0.031313 2.7671 -72.815
## - HOXB5 1 0.044757 2.7805 -72.645
## - ATRX 1 0.081205 2.8170 -72.189
## <none> 2.7357 -71.213
## - YPEL1 1 0.171775 2.9075 -71.082
## - FTSJ1 1 0.183246 2.9190 -70.944
## - PNISR 1 0.221272 2.9570 -70.491
##
## Step: AIC=-73.02
## BA ~ HOXB5 + PNISR + ATRX + PLK1S1 + ZFHX4 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - ZFHX4 1 0.02825 2.7789 -74.665
## - HOXB5 1 0.04052 2.7912 -74.511
## - PLK1S1 1 0.05611 2.8068 -74.316
## - ATRX 1 0.13350 2.8841 -73.364
## - YPEL1 1 0.15739 2.9080 -73.075
## <none> 2.7506 -73.023
## - FTSJ1 1 0.31935 3.0700 -71.178
## - PNISR 1 0.90015 3.6508 -65.114
##
## Step: AIC=-74.67
## BA ~ HOXB5 + PNISR + ATRX + PLK1S1 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - HOXB5 1 0.02391 2.8028 -76.365
## - PLK1S1 1 0.03749 2.8164 -76.196
## - YPEL1 1 0.14939 2.9283 -74.832
## <none> 2.7789 -74.665
## - ATRX 1 0.19488 2.9738 -74.293
## - FTSJ1 1 0.29613 3.0750 -73.121
## - PNISR 1 0.89851 3.6774 -66.860
##
## Step: AIC=-76.37
## BA ~ PNISR + ATRX + PLK1S1 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - PLK1S1 1 0.05400 2.8568 -77.698
## - YPEL1 1 0.15995 2.9628 -76.423
## <none> 2.8028 -76.365
## - ATRX 1 0.17201 2.9748 -76.281
## - FTSJ1 1 0.28291 3.0857 -75.000
## - PNISR 1 1.01508 3.8179 -67.548
##
## Step: AIC=-77.7
## BA ~ PNISR + ATRX + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - ATRX 1 0.11974 2.9766 -78.260
## <none> 2.8568 -77.698
## - YPEL1 1 0.26844 3.1252 -76.554
## - FTSJ1 1 0.50227 3.3591 -74.029
## - PNISR 1 0.96156 3.8184 -69.543
##
## Step: AIC=-78.26
## BA ~ PNISR + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## <none> 2.9766 -78.260
## - YPEL1 1 0.18969 3.1662 -78.098
## - FTSJ1 1 0.39421 3.3708 -75.907
## - PNISR 1 1.59191 4.5685 -65.266We kunnen ook stapsgewijze modelselectie doen startende vanaf het meest eenvoudige model:
mForStep <- step(m1,scope=list(lower=formula(m1),upper=formula(mfull)), direction="both")## Start: AIC=-19.33
## BA ~ 1
##
## Df Sum of Sq RSS AIC
## + LOC100505650 1 14.668 4.3588 -68.910
## + PNISR 1 14.376 4.6505 -66.643
## + ATRX 1 14.104 4.9231 -64.650
## + ZFHX4 1 13.869 5.1574 -63.022
## + PLK1S1 1 13.860 5.1671 -62.956
## + FTSJ1 1 13.781 5.2459 -62.426
## + BSDC1 1 13.703 5.3234 -61.913
## + DNAJC12 1 13.412 5.6141 -60.052
## + HOXB5 1 13.400 5.6263 -59.976
## + YPEL1 1 13.049 5.9774 -57.858
## <none> 19.0266 -19.333
##
## Step: AIC=-68.91
## BA ~ LOC100505650
##
## Df Sum of Sq RSS AIC
## + YPEL1 1 1.2048 3.1540 -78.233
## + DNAJC12 1 0.9106 3.4482 -75.112
## + PLK1S1 1 0.8103 3.5485 -74.109
## + FTSJ1 1 0.7896 3.5692 -73.905
## + BSDC1 1 0.7576 3.6012 -73.592
## + HOXB5 1 0.6993 3.6595 -73.031
## + ZFHX4 1 0.6990 3.6599 -73.027
## + ATRX 1 0.6328 3.7261 -72.400
## + PNISR 1 0.3633 3.9955 -69.956
## <none> 4.3588 -68.910
## - LOC100505650 1 14.6678 19.0266 -19.333
##
## Step: AIC=-78.23
## BA ~ LOC100505650 + YPEL1
##
## Df Sum of Sq RSS AIC
## <none> 3.1540 -78.233
## + PNISR 1 0.13303 3.0210 -77.741
## + HOXB5 1 0.11633 3.0377 -77.548
## + FTSJ1 1 0.06306 3.0910 -76.940
## + ATRX 1 0.04898 3.1051 -76.781
## + DNAJC12 1 0.04435 3.1097 -76.729
## + ZFHX4 1 0.02923 3.1248 -76.559
## + BSDC1 1 0.02903 3.1250 -76.557
## + PLK1S1 1 0.02578 3.1283 -76.520
## - YPEL1 1 1.20478 4.3588 -68.910
## - LOC100505650 1 2.82334 5.9774 -57.858Nu stapsgewijze modelselectie startende vanaf het meest complexe model:
mBackStep <- step(mfull,scope=list(lower=formula(m1),upper=formula(mfull)), direction="both")## Start: AIC=-67.34
## BA ~ HOXB5 + PNISR + ATRX + LOC100505650 + PLK1S1 + DNAJC12 +
## ZFHX4 + BSDC1 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - BSDC1 1 0.003369 2.7288 -69.302
## - DNAJC12 1 0.005688 2.7312 -69.272
## - LOC100505650 1 0.014735 2.7402 -69.156
## - PLK1S1 1 0.025044 2.7505 -69.025
## - ZFHX4 1 0.030840 2.7563 -68.951
## - HOXB5 1 0.039762 2.7652 -68.838
## - ATRX 1 0.063271 2.7887 -68.542
## - YPEL1 1 0.139909 2.8654 -67.593
## - FTSJ1 1 0.157697 2.8832 -67.376
## <none> 2.7255 -67.345
## - PNISR 1 0.211967 2.9374 -66.723
##
## Step: AIC=-69.3
## BA ~ HOXB5 + PNISR + ATRX + LOC100505650 + PLK1S1 + DNAJC12 +
## ZFHX4 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - DNAJC12 1 0.006916 2.7357 -71.213
## - LOC100505650 1 0.014255 2.7431 -71.119
## - PLK1S1 1 0.025052 2.7539 -70.982
## - ZFHX4 1 0.028026 2.7569 -70.944
## - HOXB5 1 0.036934 2.7658 -70.831
## - ATRX 1 0.087988 2.8168 -70.191
## - YPEL1 1 0.136972 2.8658 -69.587
## - FTSJ1 1 0.155963 2.8848 -69.356
## <none> 2.7288 -69.302
## - PNISR 1 0.228042 2.9569 -68.492
## + BSDC1 1 0.003369 2.7255 -67.345
##
## Step: AIC=-71.21
## BA ~ HOXB5 + PNISR + ATRX + LOC100505650 + PLK1S1 + ZFHX4 + FTSJ1 +
## YPEL1
##
## Df Sum of Sq RSS AIC
## - LOC100505650 1 0.014893 2.7506 -73.023
## - ZFHX4 1 0.025561 2.7613 -72.887
## - PLK1S1 1 0.031313 2.7671 -72.815
## - HOXB5 1 0.044757 2.7805 -72.645
## - ATRX 1 0.081205 2.8170 -72.189
## <none> 2.7357 -71.213
## - YPEL1 1 0.171775 2.9075 -71.082
## - FTSJ1 1 0.183246 2.9190 -70.944
## - PNISR 1 0.221272 2.9570 -70.491
## + DNAJC12 1 0.006916 2.7288 -69.302
## + BSDC1 1 0.004597 2.7312 -69.272
##
## Step: AIC=-73.02
## BA ~ HOXB5 + PNISR + ATRX + PLK1S1 + ZFHX4 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - ZFHX4 1 0.02825 2.7789 -74.665
## - HOXB5 1 0.04052 2.7912 -74.511
## - PLK1S1 1 0.05611 2.8068 -74.316
## - ATRX 1 0.13350 2.8841 -73.364
## - YPEL1 1 0.15739 2.9080 -73.075
## <none> 2.7506 -73.023
## + LOC100505650 1 0.01489 2.7358 -71.213
## - FTSJ1 1 0.31935 3.0700 -71.178
## + DNAJC12 1 0.00755 2.7431 -71.119
## + BSDC1 1 0.00409 2.7466 -71.075
## - PNISR 1 0.90015 3.6508 -65.114
##
## Step: AIC=-74.67
## BA ~ HOXB5 + PNISR + ATRX + PLK1S1 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - HOXB5 1 0.02391 2.8028 -76.365
## - PLK1S1 1 0.03749 2.8164 -76.196
## - YPEL1 1 0.14939 2.9283 -74.832
## <none> 2.7789 -74.665
## - ATRX 1 0.19488 2.9738 -74.293
## - FTSJ1 1 0.29613 3.0750 -73.121
## + ZFHX4 1 0.02825 2.7506 -73.023
## + LOC100505650 1 0.01759 2.7613 -72.887
## + DNAJC12 1 0.00489 2.7740 -72.727
## + BSDC1 1 0.00072 2.7782 -72.674
## - PNISR 1 0.89851 3.6774 -66.860
##
## Step: AIC=-76.37
## BA ~ PNISR + ATRX + PLK1S1 + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - PLK1S1 1 0.05400 2.8568 -77.698
## - YPEL1 1 0.15995 2.9628 -76.423
## <none> 2.8028 -76.365
## - ATRX 1 0.17201 2.9748 -76.281
## - FTSJ1 1 0.28291 3.0857 -75.000
## + HOXB5 1 0.02391 2.7789 -74.665
## + LOC100505650 1 0.01287 2.7899 -74.526
## + ZFHX4 1 0.01165 2.7912 -74.511
## + DNAJC12 1 0.01066 2.7921 -74.499
## + BSDC1 1 0.00070 2.8021 -74.374
## - PNISR 1 1.01508 3.8179 -67.548
##
## Step: AIC=-77.7
## BA ~ PNISR + ATRX + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## - ATRX 1 0.11974 2.9766 -78.260
## <none> 2.8568 -77.698
## - YPEL1 1 0.26844 3.1252 -76.554
## + PLK1S1 1 0.05400 2.8028 -76.365
## + HOXB5 1 0.04042 2.8164 -76.196
## + LOC100505650 1 0.03471 2.8221 -76.125
## + BSDC1 1 0.03081 2.8260 -76.077
## + DNAJC12 1 0.02797 2.8288 -76.042
## + ZFHX4 1 0.00022 2.8566 -75.700
## - FTSJ1 1 0.50227 3.3591 -74.029
## - PNISR 1 0.96156 3.8184 -69.543
##
## Step: AIC=-78.26
## BA ~ PNISR + FTSJ1 + YPEL1
##
## Df Sum of Sq RSS AIC
## <none> 2.9766 -78.260
## - YPEL1 1 0.18969 3.1662 -78.098
## + ATRX 1 0.11974 2.8568 -77.698
## + LOC100505650 1 0.08940 2.8871 -77.328
## + ZFHX4 1 0.04005 2.9365 -76.735
## + BSDC1 1 0.00413 2.9724 -76.309
## + HOXB5 1 0.00203 2.9745 -76.284
## + PLK1S1 1 0.00173 2.9748 -76.281
## + DNAJC12 1 0.00061 2.9759 -76.268
## - FTSJ1 1 0.39421 3.3708 -75.907
## - PNISR 1 1.59191 4.5685 -65.266mForward ##
## Call:
## lm(formula = BA ~ LOC100505650 + YPEL1, data = mcx)
##
## Coefficients:
## (Intercept) LOC100505650 YPEL1
## -32.240 1.671 2.337mBackward##
## Call:
## lm(formula = BA ~ PNISR + FTSJ1 + YPEL1, data = mcx)
##
## Coefficients:
## (Intercept) PNISR FTSJ1 YPEL1
## -6.538 2.165 -1.784 1.240mForStep##
## Call:
## lm(formula = BA ~ LOC100505650 + YPEL1, data = mcx)
##
## Coefficients:
## (Intercept) LOC100505650 YPEL1
## -32.240 1.671 2.337mBackStep##
## Call:
## lm(formula = BA ~ PNISR + FTSJ1 + YPEL1, data = mcx)
##
## Coefficients:
## (Intercept) PNISR FTSJ1 YPEL1
## -6.538 2.165 -1.784 1.24011.3.3 Alternatieve criteria
Recent zijn er binnen de machine learning diverse alternatieve technieken voor modelbouw ontwikkeld die hoofdzakelijk steunen op crossvalidatie, d.i. een techniek waarbij men telkens het regressiemodel schat op basis van een subset van de observaties en haar performantie evalueert door na te gaan hoe goed ze de resterende observaties voorspelt. Deze methoden zijn nog beter geschikt voor het bouwen van predictiemodellen. Ze evalueren het model immers op data die het model nog niet heeft gezien tijdens de training (fitting) fase.
Davenas, E., F. Beauvais, J. Amara, M. Oberbaum, B. Robinzon, A. Miadonnai, A. Tedeschi, et al. 1988. “Human Basophil Degranulation Triggered by Very Dilute Antiserum Against Ige.” Nature 333 (6176): 816–18. http://dx.doi.org/10.1038/333816a0.
Jacques, S., B. Ghesquière, P. De Bock, H. Demol, K. Wahni, P. Willems, J. Messens, F. Van Breusegem, and K. Gevaert. 2015. “Protein Methionine Sulfoxide Dynamics in Arabidopsis Thaliana Under Oxidative Stress.” Molecular and Cellular Proteomics 14 (5): 1217–29.
Rogovin, Konstantin A., Anastasiya M. Khrushchova, Olga N. Shekarova, Nina A. Vasilieva, and Nina Yu Vasilieva. 2017. “Females Choose Gentle, but Not Healthy or Macho Males in Campbell Dwarf Hamsters (Phodopus Campbelli Thomas 1905).” Current Zoology 63 (5): 545–54. doi:10.1093/cz/zow090.
Sotiriou, Christos, Pratyaksha Wirapati, Sherene Loi, Adrian Harris, Steve Fox, Johanna Smeds, Hans Nordgren, et al. 2006. “Gene Expression Profiling in Breast Cancer: Understanding the Molecular Basis of Histologic Grade to Improve Prognosis.” Journal of the National Cancer Institute 98 (4). Functional Genomics; Translational Research Unit, Universite Libre de Bruxelles, Brussels, Belgium. christos.sotiriou@bordet.be: 262–72. doi:10.1093/jnci/djj052.
Valdés-López, O., S. Khan, R. Schmitz, S. Cui, J. Qiu, T. Joshi, D. Xu, B. Diers, J. Ecker, and G. Stacey. 2014. “Genotypic Variation of Gene Expression During the Soybean Innate Immunity Response.” Plant Genetic Resources 12 (S1): S27–S30.