Technical details on linear regression for proteomics when starting from summarized protein expression values

1 Preamble

Read stored results for heart data

library(tidyverse)
library(limma)
library(QFeatures)
library(msqrob2)
pe <- readRDS(
  url(
    "https://raw.githubusercontent.com/statOmics/SGA2020/gh-pages/assets/peHeart.rds",
    "rb")
  )

2 Linear regression

• Consider a vector of predictors \(\mathbf{x}_i=(x_1,\ldots,x_{p-1})\) and
• a real-valued response \(Y_i\)
• with \(i = 1, \ldots, n\)
• then the linear regression model can be written as \[ Y_i=f(\mathbf{x}) +\epsilon=\beta_0+\sum\limits_{j=1}^{p-1} x_{ij}\beta + \epsilon_i \] with i.i.d. \(\epsilon_i\sim N(0,\sigma^2)\)

---

• \(n\) observations \((\mathbf{x}_1,y_1) \ldots (\mathbf{x}_n,y_n)\)
• Regression in matrix notation \[\mathbf{Y}=\mathbf{X\beta} + \boldsymbol{\epsilon}\] with \(\mathbf{Y}=\left[\begin{array}{c}y_1\\ \vdots\\y_n\end{array}\right]\), \(\mathbf{X}=\left[\begin{array}{cccc} 1&x_{11}&\ldots&x_{1p-1}\\ \vdots&\vdots&&\vdots\\ 1&x_{n1}&\ldots&x_{np-1} \end{array}\right]\), \(\boldsymbol{\beta}=\left[\begin{array}{c}\beta_0\\ \vdots\\ \beta_{p-1}\end{array}\right]\) and \(\boldsymbol{\epsilon}=\left[\begin{array}{c} \epsilon_1 \\ \vdots \\ \epsilon_n\end{array}\right]\)

---

2.1 Least Squares (LS)

• Minimize the residual sum of squares \[\begin{eqnarray*} RSS(\boldsymbol{\beta})&=&\sum\limits_{i=1}^n e^2_i\\ &=&\sum\limits_{i=1}^n \left(y_i-\beta_0-\sum\limits_{j=1}^p x_{ij}\beta_j\right)^2 \end{eqnarray*}\]

• or in matrix notation \[\begin{eqnarray*} RSS(\boldsymbol{\beta})&=&(\mathbf{Y}-\mathbf{X\beta})^T(\mathbf{Y}-\mathbf{X\beta})\\ &=&\Vert \mathbf{Y}-\mathbf{X\beta}\Vert^2 \end{eqnarray*}\] with the \(L_2\)-norm of a \(p\)-dim. vector \(v\) \(\Vert \mathbf{v} \Vert=\sqrt{v_1^2+\ldots+v_p^2}\)

• \(\rightarrow\) \(\hat{\boldsymbol{\beta}}=\text{argmin}_\beta \Vert \mathbf{Y}-\mathbf{X\beta}\Vert^2\)}

---

2.1.1 Minimize RSS

\[ \begin{array}{ccc} \frac{\partial RSS}{\partial \boldsymbol{\beta}}&=&\mathbf{0}\\\\ \frac{(\mathbf{Y}-\mathbf{X\beta})^T(\mathbf{Y}-\mathbf{X\beta})}{\partial \boldsymbol{\beta}}&=&\mathbf{0}\\\\ -2\mathbf{X}^T(\mathbf{Y}-\mathbf{X\beta})&=&\mathbf{0}\\\\ \mathbf{X}^T\mathbf{X\beta}&=&\mathbf{X}^T\mathbf{Y}\\\\ \hat{\boldsymbol{\beta}}&=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y} \end{array} \]

---

2.1.1.1 Heart example

y <- assay(pe[["proteinRobust"]])[2,]
fit <- lm(y ~ location*tissue + patient, data = colData(pe), x = TRUE)
head(fit$x,4)

##               (Intercept) locationR tissueV patient4 patient8 locationR:tissueV
## Intensity.LA3           1         0       0        0        0                 0
## Intensity.LA4           1         0       0        1        0                 0
## Intensity.LA8           1         0       0        0        1                 0
## Intensity.LV3           1         0       1        0        0                 0

The model matrix can also be obtained without fitting the model:

X <- model.matrix(~ location * tissue + patient, colData(pe))
head(X,4)

##               (Intercept) locationR tissueV patient4 patient8 locationR:tissueV
## Intensity.LA3           1         0       0        0        0                 0
## Intensity.LA4           1         0       0        1        0                 0
## Intensity.LA8           1         0       0        0        1                 0
## Intensity.LV3           1         0       1        0        0                 0

Least squares:

betas <- solve(t(X)%*%X) %*% t(X) %*% y
cbind(fit$coef, betas)

##                          [,1]        [,2]
## (Intercept)       26.57559360 26.57559360
## locationR          0.20636497  0.20636497
## tissueV            0.12756675  0.12756675
## patient4           0.30592435  0.30592435
## patient8          -0.33432636 -0.33432636
## locationR:tissueV -0.04130843 -0.04130843

---

2.1.2 Variance Estimator?

\[ \begin{array}{ccl} \hat{\boldsymbol{\Sigma}}_{\hat{\boldsymbol{\beta}}} &=&\text{var}\left[(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\right]\\\\ &=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\text{var}\left[\mathbf{Y}\right]\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\\\\ &=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T(\mathbf{I}\sigma^2)\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1} \\\\ &=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{I}\quad\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\sigma^2\\\\ %\hat{\boldmath{\Sigma}}_{\hat{\boldsymbol{\beta}}}&=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\var\left[\mathbf{Y}\right](\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}\\ &=&(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\sigma^2\\\\ &=&(\mathbf{X}^T\mathbf{X})^{-1}\sigma^2 \end{array} \]

---

2.1.2.1 Heart example

summary(fit)$cov.unscaled * sigma(fit)^2

##                   (Intercept)     locationR       tissueV      patient4
## (Intercept)         0.3938774 -2.625849e-01 -2.625849e-01 -1.969387e-01
## locationR          -0.2625849  5.251699e-01  2.625849e-01  9.179357e-17
## tissueV            -0.2625849  2.625849e-01  5.251699e-01  6.475378e-17
## patient4           -0.1969387  9.179357e-17  6.475378e-17  3.938774e-01
## patient8           -0.1969387  1.372344e-16  1.337955e-16  1.969387e-01
## locationR:tissueV   0.2625849 -5.251699e-01 -5.251699e-01  3.121582e-17
##                        patient8 locationR:tissueV
## (Intercept)       -1.969387e-01      2.625849e-01
## locationR          1.372344e-16     -5.251699e-01
## tissueV            1.337955e-16     -5.251699e-01
## patient4           1.969387e-01      3.121582e-17
## patient8           3.938774e-01     -1.321146e-16
## locationR:tissueV -1.321146e-16      1.050340e+00

n <- nrow(X)
p <- ncol(X)
mse <- sum((y-X%*%betas)^2)/(n-p)
SigmaBeta <- solve(t(X)%*%X) * mse   
SigmaBeta

##                   (Intercept)     locationR       tissueV   patient4   patient8
## (Intercept)         0.3938774 -2.625849e-01 -2.625849e-01 -0.1969387 -0.1969387
## locationR          -0.2625849  5.251699e-01  2.625849e-01  0.0000000  0.0000000
## tissueV            -0.2625849  2.625849e-01  5.251699e-01  0.0000000  0.0000000
## patient4           -0.1969387 -4.372918e-17 -4.372918e-17  0.3938774  0.1969387
## patient8           -0.1969387 -4.372918e-17 -4.372918e-17  0.1969387  0.3938774
## locationR:tissueV   0.2625849 -5.251699e-01 -5.251699e-01  0.0000000  0.0000000
##                   locationR:tissueV
## (Intercept)            2.625849e-01
## locationR             -5.251699e-01
## tissueV               -5.251699e-01
## patient4               4.372918e-17
## patient8               4.372918e-17
## locationR:tissueV      1.050340e+00

range(SigmaBeta - summary(fit)$cov.unscaled * sigma(fit)^2)

## [1] -1.998401e-15  3.774758e-15

data.frame(summary(fit)$coef[,1:2], betas = betas, seBetas = diag(SigmaBeta)^.5)

2.2 Contrasts

When we assess a contrast we assess a linear combination of model parameters:

\[ H_0: \mathbf{L^T\beta} = 0 \text{ vs } H_1: \mathbf{L^T\beta} \neq 0 \]

Estimator of Contrast?

\[\mathbf{L}^T\hat{\boldsymbol{\beta}}\]

Variance?

\[ \boldsymbol{\Sigma}_{\mathbf{L}\hat{\boldsymbol{\beta}}}=\mathbf{L}^T\boldsymbol{\Sigma}_{\hat{\boldsymbol{\beta}}}\mathbf{L} \]

---

2.2.1 Heart example

L <- makeContrast(
  c(
    "tissueV = 0",
    "tissueV + locationR:tissueV = 0",
    "tissueV + 0.5*locationR:tissueV = 0","locationR:tissueV = 0"),
  parameterNames =
    rowData(pe[["proteinRobust"]])$msqrobModels[[2]] %>%
    getCoef %>%
    names
  )
L

##                   tissueV tissueV + locationR:tissueV
## (Intercept)             0                           0
## locationR               0                           0
## tissueV                 1                           1
## patient4                0                           0
## patient8                0                           0
## locationR:tissueV       0                           1
##                   tissueV + 0.5 * locationR:tissueV locationR:tissueV
## (Intercept)                                     0.0                 0
## locationR                                       0.0                 0
## tissueV                                         1.0                 0
## patient4                                        0.0                 0
## patient8                                        0.0                 0
## locationR:tissueV                               0.5                 1

contrasts <- t(L) %*% betas
SigmaContrasts <- t(L) %*% SigmaBeta %*% L
seContrasts <- SigmaContrasts %>%
  diag %>%
  sqrt

Comparison with lm and glht results

library(multcomp)

## Loading required package: mvtnorm

## Warning: package 'mvtnorm' was built under R version 4.4.1

## Loading required package: survival

## Loading required package: TH.data

## Loading required package: MASS

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

## 
## Attaching package: 'TH.data'

## The following object is masked from 'package:MASS':
## 
##     geyser

fitGlht <- glht(fit, linfct = t(L))
summary(fitGlht, test = adjusted("none"))

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Fit: lm(formula = y ~ location * tissue + patient, data = colData(pe), 
##     x = TRUE)
## 
## Linear Hypotheses:
##                                        Estimate Std. Error t value Pr(>|t|)
## tissueV == 0                            0.12757    0.72469   0.176    0.866
## tissueV + locationR:tissueV == 0        0.08626    0.72469   0.119    0.909
## tissueV + 0.5 * locationR:tissueV == 0  0.10691    0.51243   0.209    0.842
## locationR:tissueV == 0                 -0.04131    1.02486  -0.040    0.969
## (Adjusted p values reported -- none method)

data.frame(contrasts, seContrasts)

• Note, that the power for assessing \(\log_2\) FC between ventriculum and atrium left and right is the same. Indeed, the standard errors are equal for both effects.

• Note, that the power for assessing \(\log_2\) FC between ventriculum and atrium over both heart regions is higher than when assessing the effect left or right.

  • Indeed, the standard error is a factor \(\sqrt{2}\) smaller for the former effect
  • We intuitively can explain this because we can use all samples (double the number of samples) to assess the average effect.
  • Hence the variance is a factor two smaller, and the se with a factor \(\sqrt{2}\)

• Note, that we have the lowest power to pick up an interaction effect. Indeed, the se is a factor \(\sqrt{2}\) larger than for the ventriculum - atrium effect left or right and a factor 2 larger than for the average effect between ventriculum and atrium.

seContrasts / seContrasts[1]

##                           tissueV       tissueV + locationR:tissueV 
##                         1.0000000                         1.0000000 
## tissueV + 0.5 * locationR:tissueV                 locationR:tissueV 
##                         0.7071068                         1.4142136

sqrt(2)

## [1] 1.414214

1/sqrt(2)

## [1] 0.7071068

2.2.2 t-tests

• When the assumptions of the linear model hold \[ \hat{\boldsymbol{\beta}} \sim MVN\left[\boldsymbol{\beta},\left(\mathbf{X}^T\mathbf{X}\right)^{-1}\sigma^2\right] \]

• Hence, \[ \mathbf{L}^T\hat{\boldsymbol{\beta}} \sim MVN\left[\mathbf{L}^T\boldsymbol{\beta},\mathbf{L}^T\left[\left(\mathbf{X}^T\mathbf{X}\right)^{-1}\sigma^2\right]\mathbf{L}\right] \]

• We estimate \(\sigma^2\) by MSE \[\hat{\sigma}^2=\frac{\mathbf{e}^T\mathbf{e}}{n-p} \rightarrow \hat{\boldsymbol{\Sigma}}_{\hat{\boldsymbol{\beta}}}=\left(\mathbf{X}^T\mathbf{X}\right)^{-1}\hat\sigma^2\]

• When we test one contrast at the time (e.g. the \(k^\text{th}\) contrast) the statistic reduces to

\[T=\frac{\mathbf{L}_k^T\hat{\boldsymbol{\beta}}}{\sqrt{\left(\mathbf{L}^T_k\hat{\boldsymbol{\Sigma}}_{\hat{\boldsymbol{\beta}}}\mathbf{L}_k\right)}} \underset{H_0}{\sim} t_{n-p}\] follows a t distribution with n-p degrees of freedom under \(H_0: \mathbf{L}^T_k\hat{\boldsymbol{\beta}}=0\)

---

2.2.2.1 Heart example

tContrasts <- contrasts/seContrasts
pContrasts <- pt(abs(tContrasts),
  df = n - p,
  lower.tail = FALSE) * 2

Comparison with lm and glht results

summary(fitGlht, test = adjusted("none"))

## 
##   Simultaneous Tests for General Linear Hypotheses
## 
## Fit: lm(formula = y ~ location * tissue + patient, data = colData(pe), 
##     x = TRUE)
## 
## Linear Hypotheses:
##                                        Estimate Std. Error t value Pr(>|t|)
## tissueV == 0                            0.12757    0.72469   0.176    0.866
## tissueV + locationR:tissueV == 0        0.08626    0.72469   0.119    0.909
## tissueV + 0.5 * locationR:tissueV == 0  0.10691    0.51243   0.209    0.842
## locationR:tissueV == 0                 -0.04131    1.02486  -0.040    0.969
## (Adjusted p values reported -- none method)

data.frame(contrasts, seContrasts, tContrasts, pContrasts)

---

3 Robust regression

• With msqrob2 we perform robust regression to estimate the model parameters of the regression model

• No normality assumption needed

• Robust fit minimises the maximal bias of the estimators

• CI and statistical tests are based on asymptotic theory

• If \(\epsilon\) is normal, the M-estimators have a high efficiency!

• ordinary least squares (OLS): minimize loss function \[\sum\limits_{i=1}^n (y_i-\mathbf{x}_i^T\boldsymbol{\beta})^2\]

• M-estimation: minimize loss function \[\sum\limits_{i=1}^n \rho\left(y_i-\mathbf{x}_i^T\boldsymbol{\beta}\right)\] with

  • \(\rho\) is symmetric, i.e. \(\rho(z)=\rho(-z)\)
  • \(\rho\) has a minimum at \(\rho(0)=0\), is positive for all \(z\neq 0\)
  • \(\rho(z)\) increases as \(\vert z\vert\) increases

---

The estimator \(\hat{\mu}\) is also the solution to the equation \[ \sum_{i=1}^n \Psi(y_i - \mathbf{x}_i\boldsymbol{\beta}) =0, \] where \(\Psi\) is the derivative of \(\rho\). For \(\hat{\beta}\) possessing the robustness property, \(\Psi\) should be bounded.

---

Example: least squares

• \(\rho(z) = z^2\), and thus \(\Psi(z)=2z\) (unbounded!). Not robust!

• \(\hat{\boldsymbol{\beta}}\) is the solution of \[ \sum_{i=1}^n 2 \mathbf{x}_i (y_i - \mathbf{x}_i^T\boldsymbol{\beta}) = 0 \text{ or } \hat{\boldsymbol{\beta}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}\mathbf{y} \] with \(\mathbf{X}=[\mathbf{x}_1 \ldots \mathbf{x}_G]^T\)

---

When a location and a scale parameter, say \(\sigma\), have to be estimated simultaneously, we write \[ (\hat{\boldsymbol{\beta}},\hat{\sigma}) = \text{ArgMin}_{\boldsymbol{\beta},\sigma} \sum_{i=1}^n \rho\left(\frac{y_i - \mathbf{x}_i^T\boldsymbol{\beta}}{\sigma}\right) \text{ and } \sum_{i=1}^n \Psi\left(\frac{y_i - \mathbf{x}_i^T\boldsymbol{\beta}}{\sigma}\right) =0. \]

Define \(u_i = \frac{y_i - \mathbf{x}_i^T\boldsymbol{\beta}}{\sigma}\). The last estimation equation is equivalent to \[ \sum_{i=1}^n w(u_i) u_i = 0 , \] with weight function \(w(u)=\Psi(u)/u\). This is the typical form that appears when solving the iteratively reweighted least squares problem, \[ (\hat{\boldsymbol{\beta}},\hat{\sigma}) = \text{ArgMin}_{\mu,\sigma} \sum_{i=1}^n w(u_i^{(k-1)}) \left(u_i^{(k)}\right)^2 , \] where \(k\) represents the iteration number.

---

3.1 Some Examples of Robust Functions

PhD thesis Bolstad 2004

---

3.2 The \(\rho\) functions

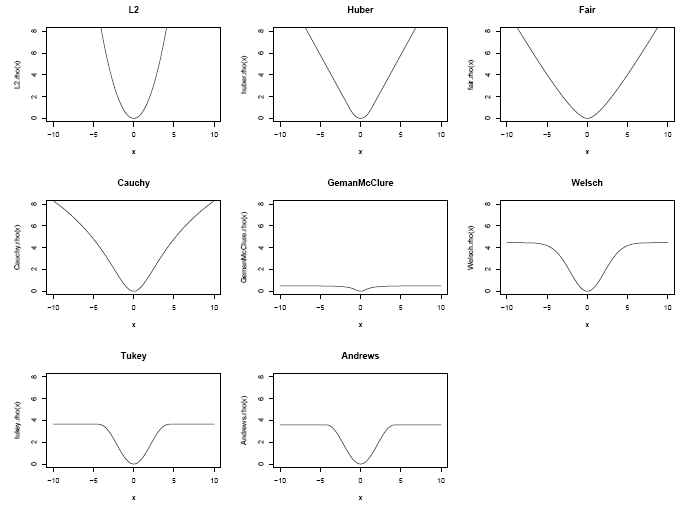
PhD thesis Bolstad 2004

---

3.2.1 Common \(\Psi\)-Functions

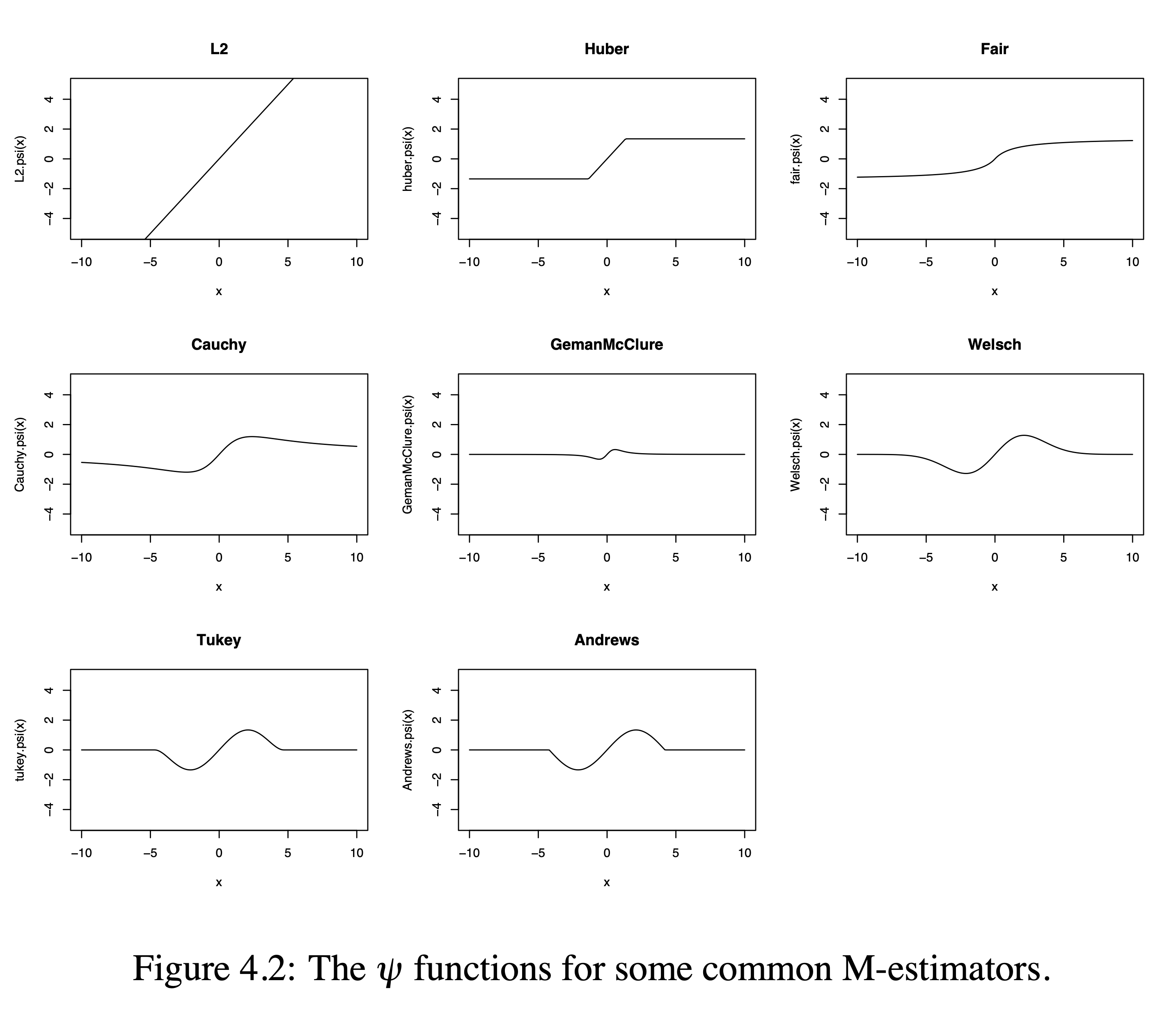
PhD thesis Bolstad 2004

---

3.2.2 Corresponding Weight Functions

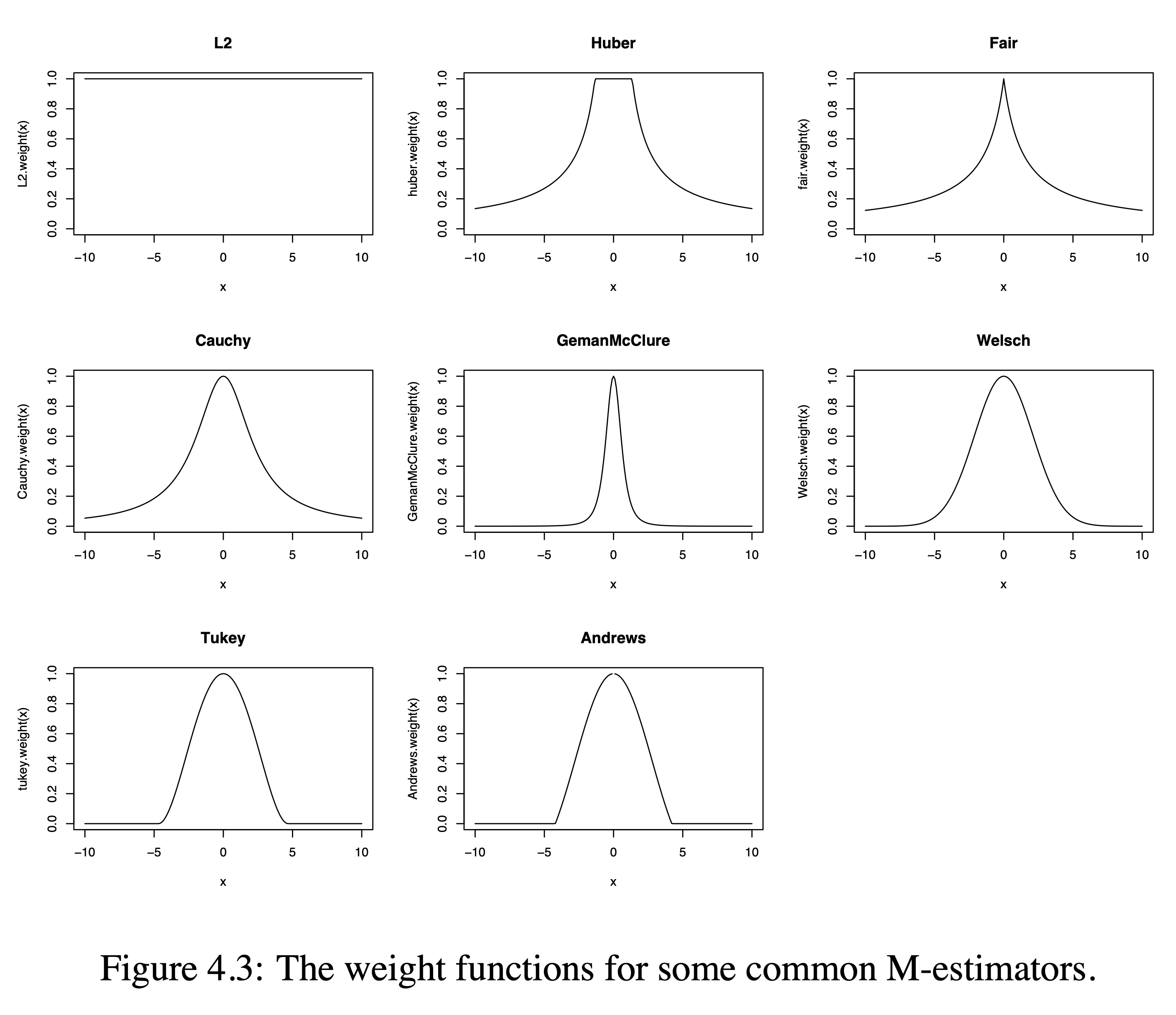
PhD thesis Bolstad 2004

---

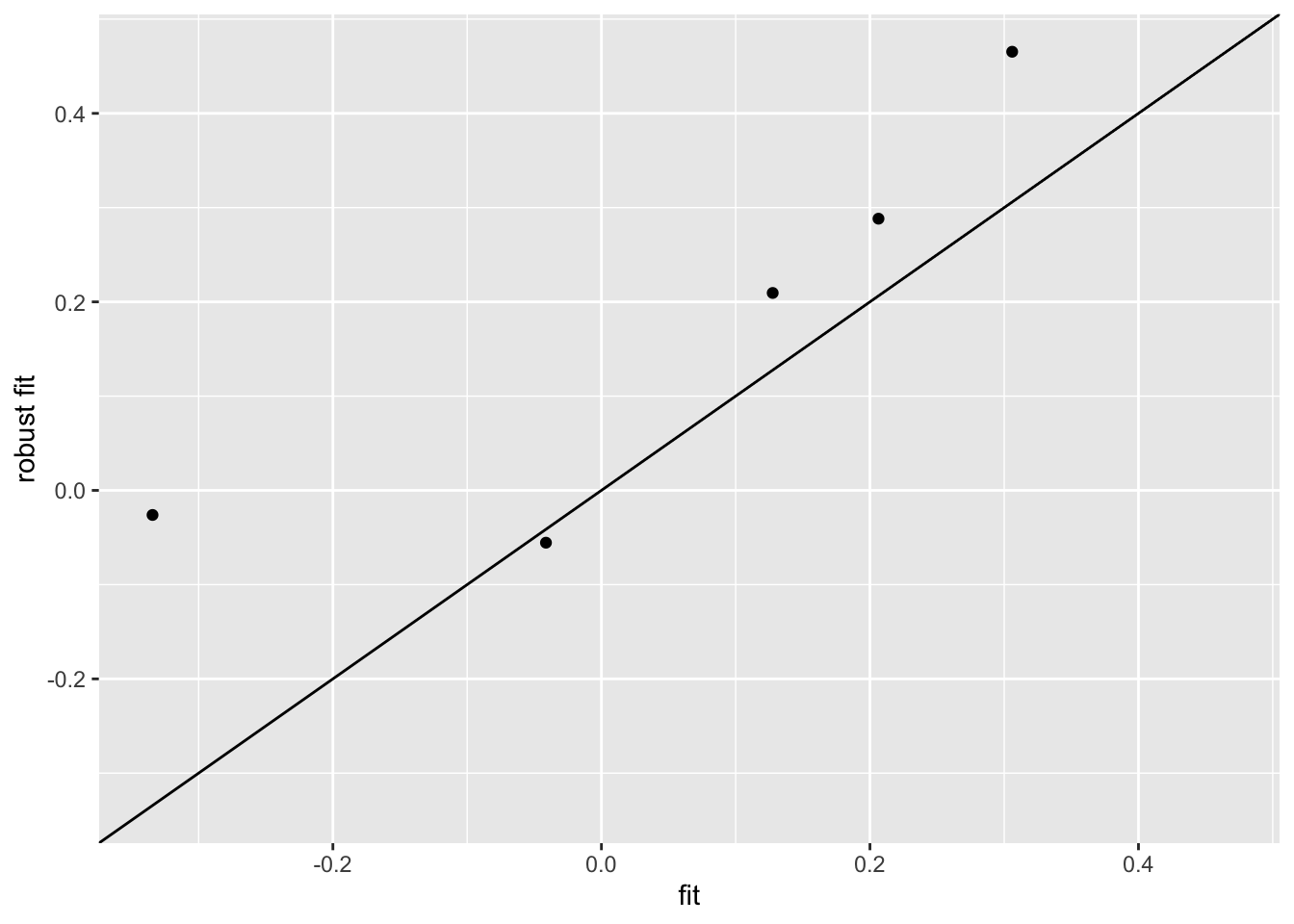
library("MASS")
rfit <- rlm(y ~ location * tissue + patient, colData(pe), maxit=1)

## Warning in rlm.default(x, y, weights, method = method, wt.method = wt.method, :
## 'rlm' failed to converge in 1 steps

qplot(fit$coefficient[-1],
  rfit$coefficient[-1],
  xlab="fit",
  ylab="robust fit") +
  geom_abline() +
  xlim(range(c(fit$coefficient[-1],rfit$coefficient[-1]))) +
  ylim(range(c(fit$coefficient[-1],rfit$coefficient[-1])))

## Warning: `qplot()` was deprecated in ggplot2 3.4.0.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

---

rfit$w

##  [1] 0.9516397 1.0000000 0.6628477 1.0000000 1.0000000 1.0000000 1.0000000
##  [8] 1.0000000 1.0000000 0.4805187 1.0000000 0.4344049

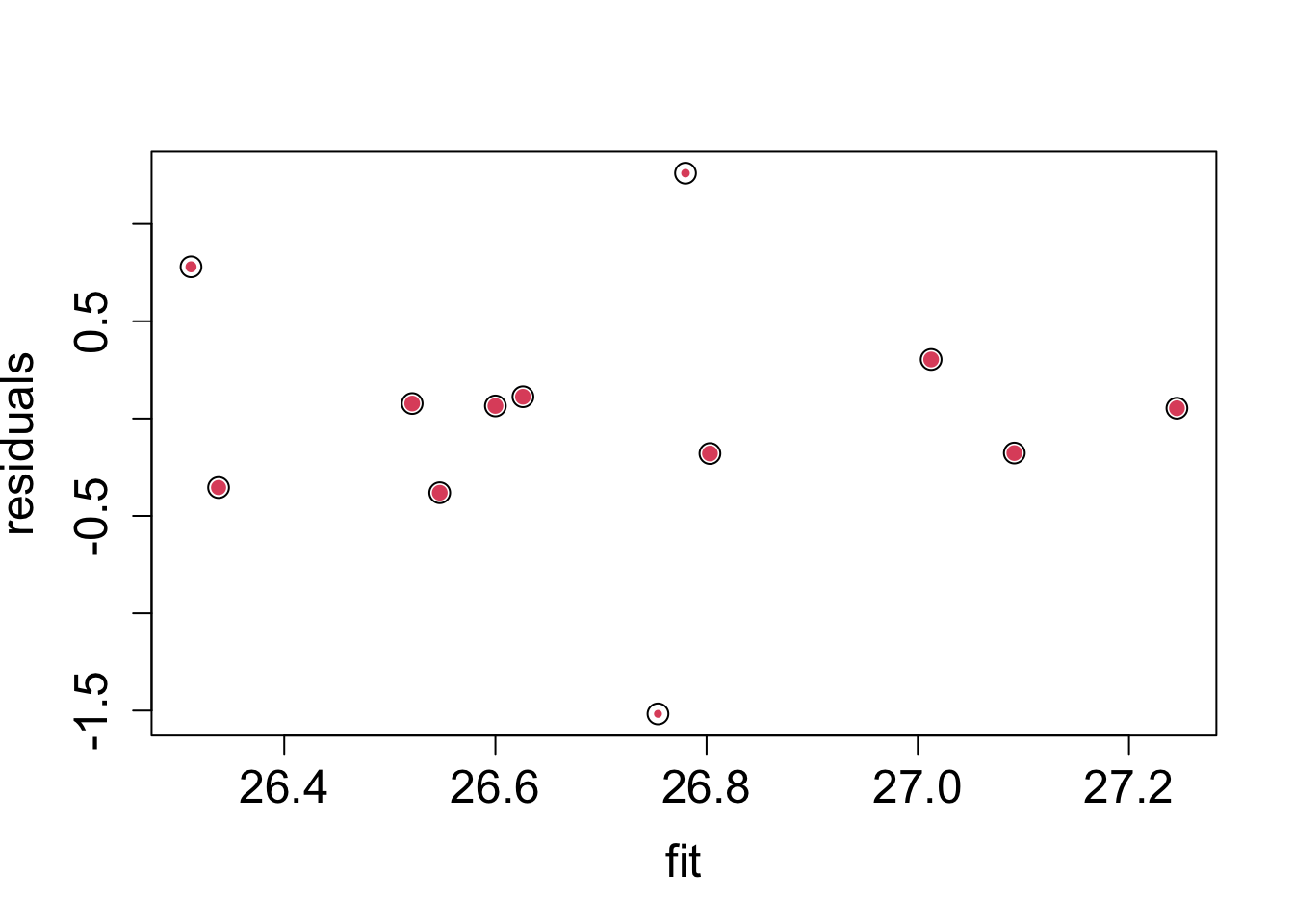
plot(
  rfit$fitted,
  rfit$res,
  cex=rfit$w,
  pch=19,col=2,
  cex.lab=1.5,
  cex.axis=1.5,
  ylab="residuals",
  xlab="fit")
points(rfit$fitted, rfit$res , cex= 1.5)

---

summary(fit)

## 
## Call:
## lm(formula = y ~ location * tissue + patient, data = colData(pe), 
##     x = TRUE)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.29698 -0.32767  0.04041  0.24905  1.17251 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)       26.57559    0.62760  42.345 1.16e-08 ***
## locationR          0.20636    0.72469   0.285    0.785    
## tissueV            0.12757    0.72469   0.176    0.866    
## patient4           0.30592    0.62760   0.487    0.643    
## patient8          -0.33433    0.62760  -0.533    0.613    
## locationR:tissueV -0.04131    1.02486  -0.040    0.969    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8876 on 6 degrees of freedom
## Multiple R-squared:  0.1687, Adjusted R-squared:  -0.524 
## F-statistic: 0.2436 on 5 and 6 DF,  p-value: 0.9286

summary(rfit)

## 
## Call: rlm(formula = y ~ location * tissue + patient, data = colData(pe), 
##     maxit = 1)
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.51703 -0.22326  0.05909  0.16009  1.26070 
## 
## Coefficients:
##                   Value   Std. Error t value
## (Intercept)       26.3378  0.5391    48.8585
## locationR          0.2883  0.6225     0.4631
## tissueV            0.2095  0.6225     0.3365
## patient4           0.4654  0.5391     0.8633
## patient8          -0.0261  0.5391    -0.0484
## locationR:tissueV -0.0555  0.8803    -0.0630
## 
## Residual standard error: 0.4189 on 6 degrees of freedom

rowData(pe[["proteinRobust"]])$msqrobModels[[2]] %>% getCoef

##       (Intercept)         locationR           tissueV          patient4 
##       26.33779939        0.28826213        0.20946392        0.46536955 
##          patient8 locationR:tissueV 
##       -0.02608046       -0.05550111

---

3.3 Understanding implementation of robust regression

3.3.1 Simulate 20 observations from a linear model with errors that follow a normal distribution

set.seed <- 112358
nobs <- 20
sdy <- 1
xsim <- seq(0, 1, length.out = nobs)
ysim <- 10 + 5*xsim + rnorm(nobs, sd = sdy)

3.3.2 add outlier at high leverage point

ysim[nobs] <- 7

3.3.3 fit linear model

ols <- lm(ysim ~ xsim)

3.3.4 fit robust linear model

library(MASS)
mEst <- rlm(ysim ~ xsim)

3.3.4.1 plot results

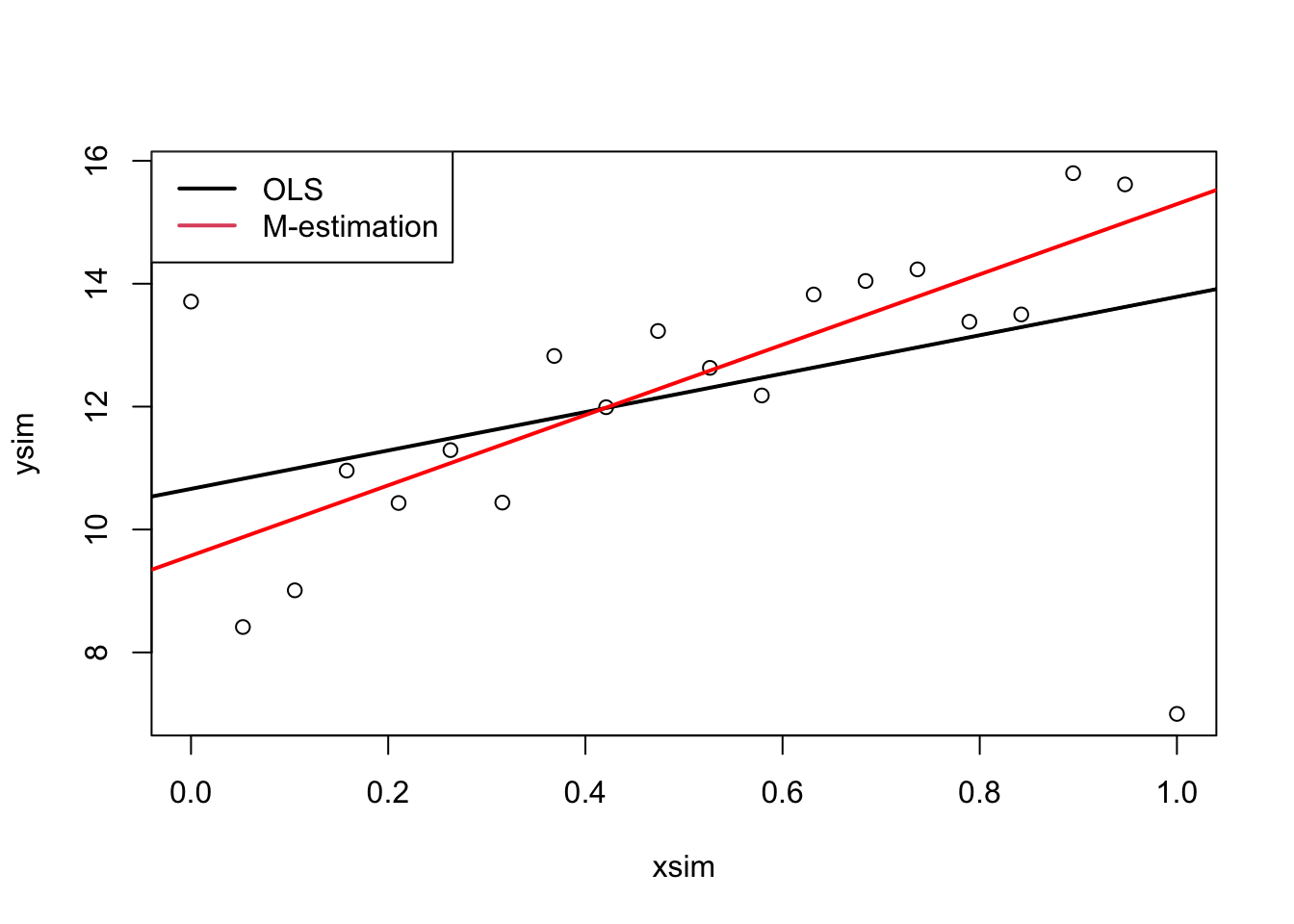
plot(xsim, ysim)
abline(ols, lwd = 2)
abline(mEst, col = "red", lwd = 2)
legend("topleft",
  legend = c("OLS", "M-estimation"),
  lwd = 2,
  col = 1:2)

round(mEst$w,3)

##  [1] 1.000 1.000 1.000 0.552 1.000 1.000 1.000 1.000 0.762 1.000 1.000 1.000
## [13] 1.000 1.000 1.000 1.000 0.793 1.000 1.000 0.122

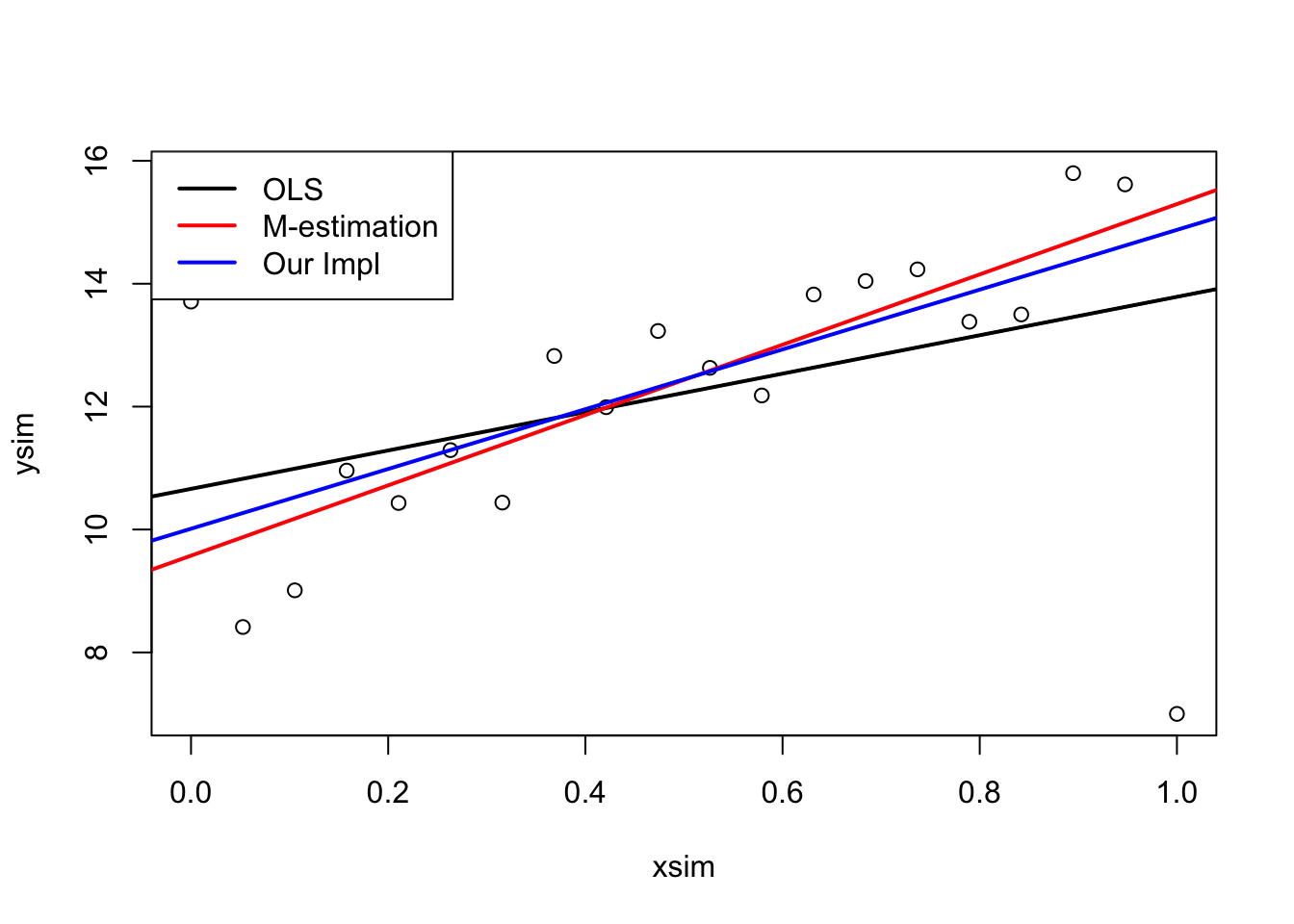
The plot clearly shows that the outlier has a high impact on the slope estimate. This is because the outlier is at a high leverage point, i.e. far from the average covariate pattern.

3.3.5 Implement it yourself

3.3.5.1 start from ols fit

lmMod <- ols

3.3.5.2 Use robust variance estimator to calculate the z

res <- lmMod$res
stdev <- mad(res)
stdev

## [1] 0.7675072

median(abs(res-median(res)))*1.4826

## [1] 0.7675072

z <- res/stdev

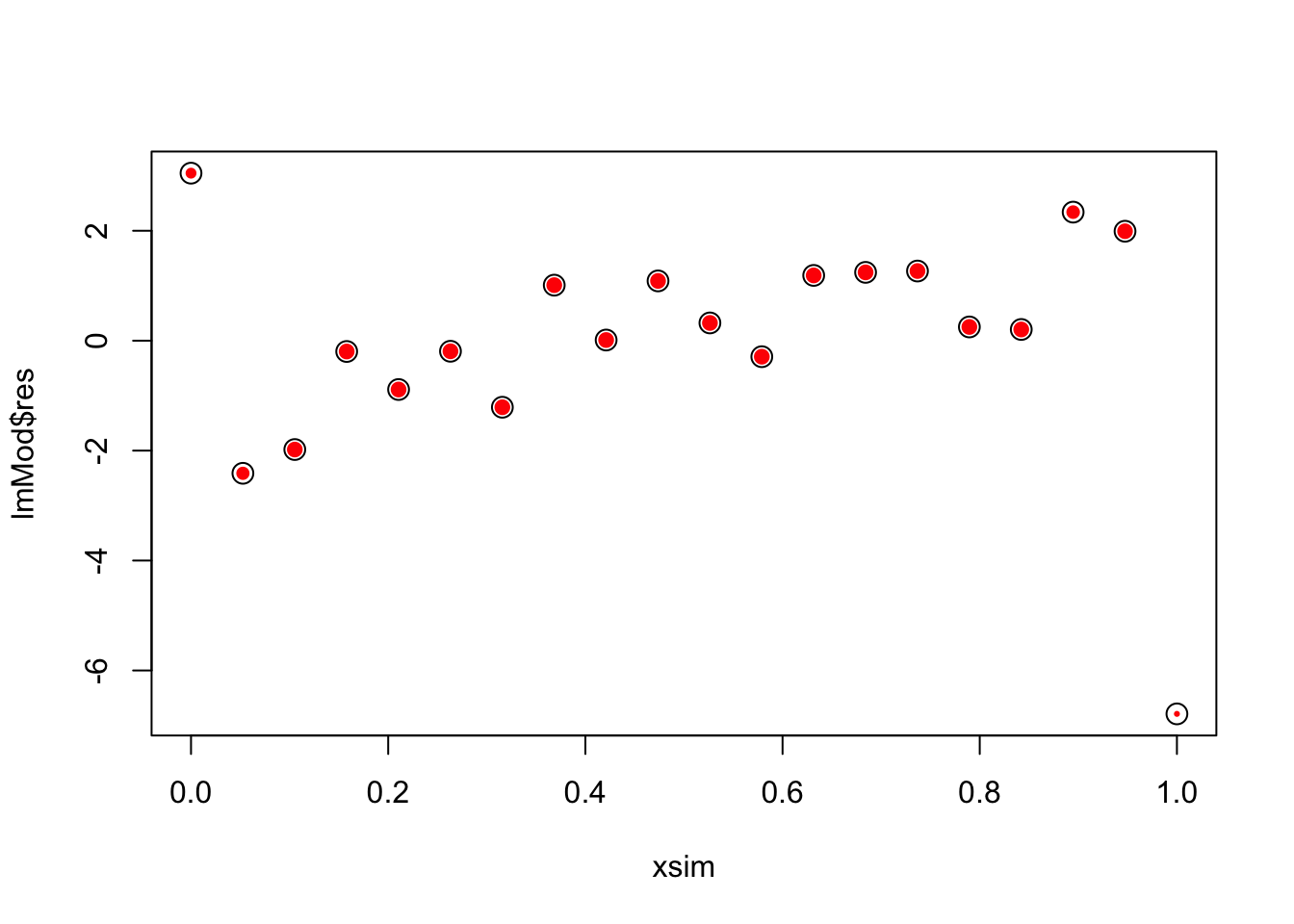
3.3.5.3 Calculate weights use psi.huber function

w <- psi.huber(z)
plot(xsim, ysim)

plot(xsim, lmMod$res, cex = w, pch = 19, col = "red")
points(xsim,lmMod$res, cex = 1.5)

3.3.5.4 Perform a weighted regression use lm with weights=w

lmMod <- lm(ysim~xsim, weights = w)

3.3.5.5 Plot results

plot(xsim, ysim)
abline(ols, lwd = 2)
abline(mEst, col = "red", lwd = 2)
abline(lmMod, col = "blue", lwd = 2)
legend("topleft",
  legend = c("OLS","M-estimation","Our Impl"),
  lwd = 2,
  col = c("black", "red", "blue"))

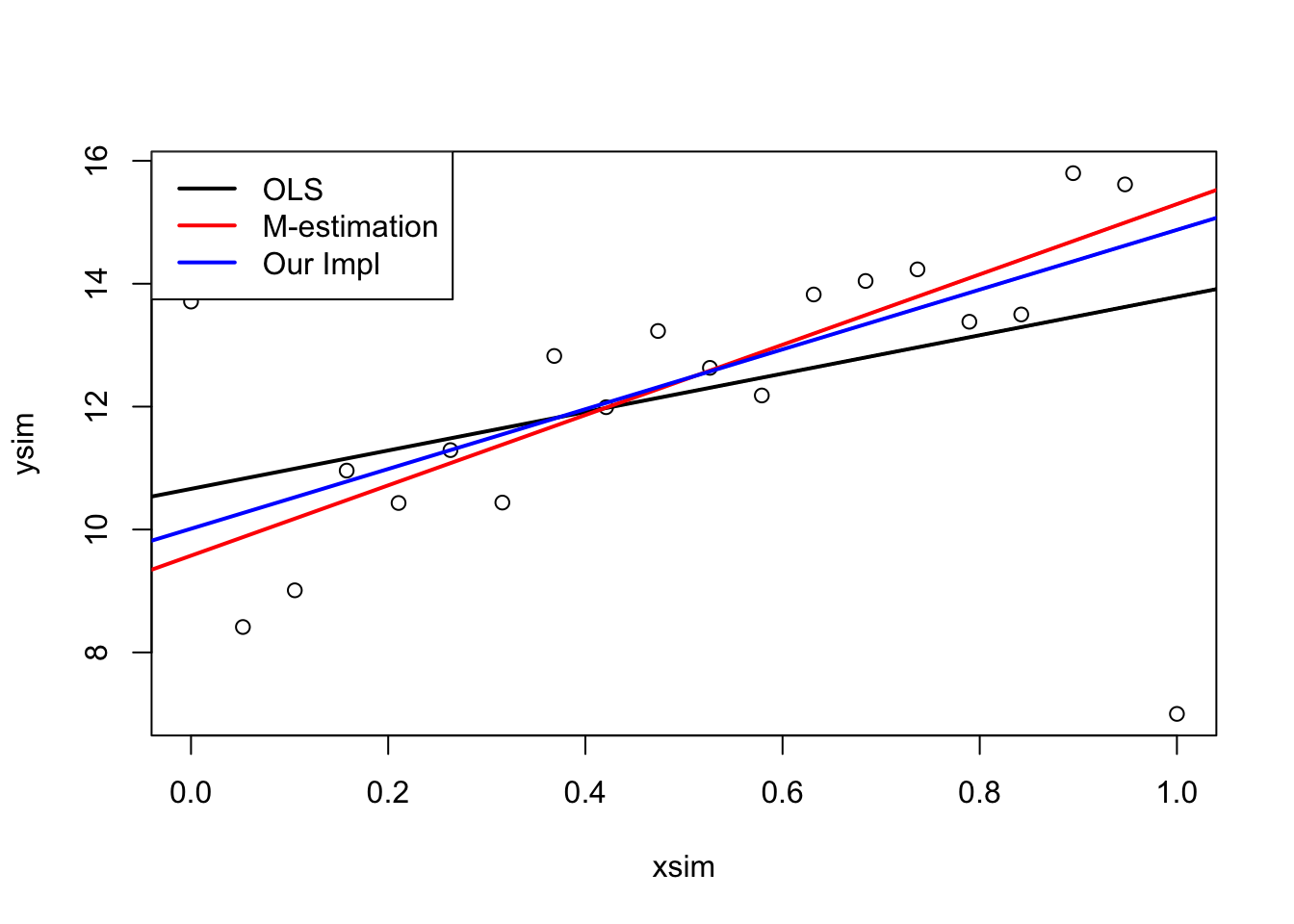
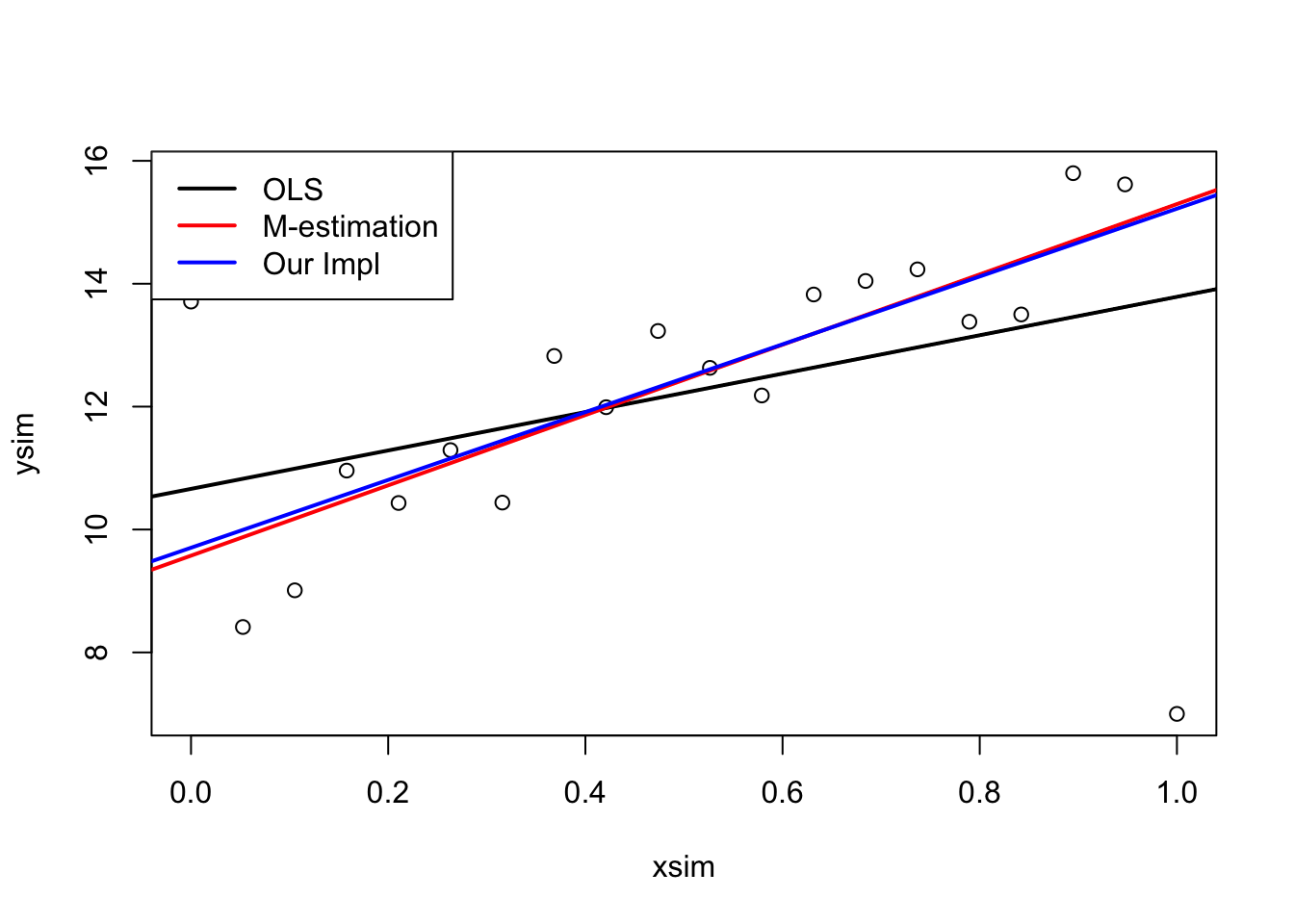
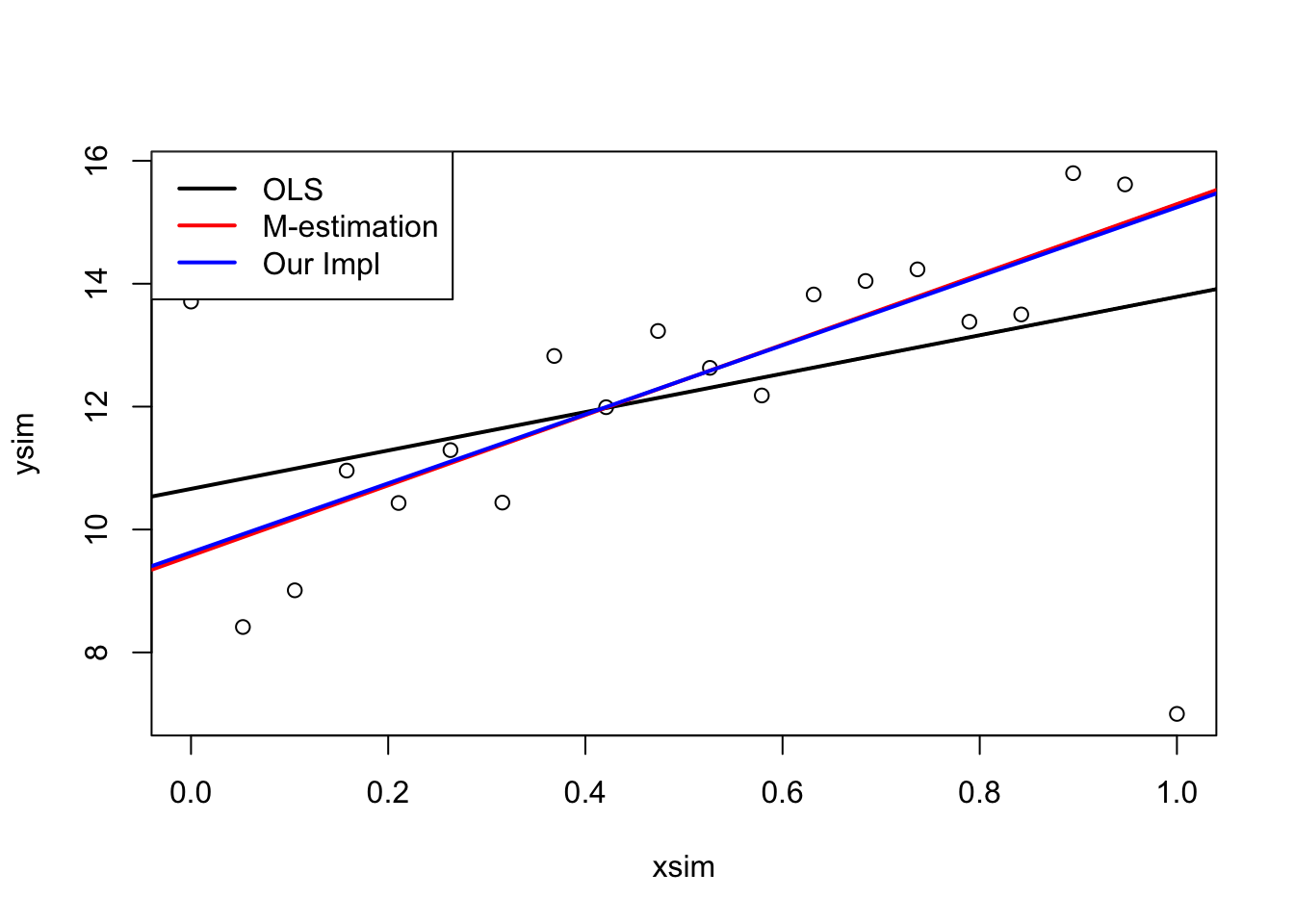
3.3.5.6 Repeat this many times

lmMod <- ols
for (k in 1:3)
{
######repeat this part several times until convergence
#use robust variance estimator to calculate the z
res <- lmMod$res
stdev <- mad(res)
median(abs(res-median(res)))*1.4826

z <- res/stdev

#calculate weights
#use psi.huber function
w <- psi.huber(z)

#perform a weighted regression use lm with weights=w
lmMod <- lm(ysim ~ xsim, weights = w)

#plot results
plot(xsim,ysim)
abline(ols, lwd = 2)
abline(mEst, col = "red", lwd = 2)
abline(lmMod, col = "blue", lwd = 2)
legend("topleft",
  legend = c("OLS","M-estimation","Our Impl"),
  lwd = 2,
  col = c("black", "red", "blue")
  )
####################################
}

4 Empirical Bayes/Moderated \(t\)-test.

A general class of moderated test statistics is given by

\[\tilde{T}_p = \frac{\mathbf{L}_k \hat{ \boldsymbol{\beta_p}}}{\mathbf{L}_k^T(\mathbf{X}^T\mathbf{WX})^{-1}\mathbf{L}_k^T \tilde{s}_p^2}\]

where \(\tilde{s}_p\) is a moderated variance estimator.

Simple approach: set \(\tilde{s}_p=s_p + s_0\): simply add a small positive constant to the denominator of the t-statistic

theory provides formal framework for borrowing strength across genes or proteins, e.g. popular bioconductor package \[\tilde{s}_g=\sqrt{\frac{d_ps_p^2+d_0s_0^2}{d_g+d_0}},\] and the moderated t-statistic is t-distributed with \(d_0+d_g\) degrees of freedom under the null hypothesis \(H_0: \mathbf{L}\boldsymbol{\beta}=0\).

• Note, that the degrees of freedom increase by borrowing strength across proteins.

---

4.1 Intermezzo: Bayesian Methods

• Frequentists consider data as random and population parameters as fixed but unknown

• In Bayesian viewpoint a person has prior beliefs about the population parameters and the uncertainty on this prior beliefs are represented by a probability distribution placed on this parameter.

  • This distribution reflects the person’s subjective prior opinion about plausible values of the parameter.
  • And is referred to as the prior \(g(\boldsymbol{\theta})\).

• Bayesian thinking will update the prior information on the population parameters by confronting the model to data (\(\mathbf{Y}\)).

• By using Bayes Theorem this results in a posterior distribution on the model parameters.
  \[ g(\boldsymbol{\theta}\vert\mathbf{Y})=\frac{f(Y\vert \boldsymbol{\theta})g(\boldsymbol{\theta})}{\int f(Y\vert \boldsymbol{\theta}) g(\boldsymbol{\theta}) d\boldsymbol{\theta}} \text{ }\left(\text{ posterior}=\frac{\text{prior} \times \text{ likelihood}}{\text{Marginal distribution}}\right) \]

---

4.2 Limma approach

Developed for gene expression analysis with micro arrays. Let g be the index for gene g. \[ \begin{array}{cc} &\beta_{gk}\vert \sigma^2_g,\beta_{gk}\neq 0 \sim N(0,v_{0k}\sigma_g^2)\\\\ \text{Prior}\\ &\frac{1}{\sigma^2_g}\sim s^2_0\frac{\chi^2_{d_0}}{d_0}\\\\\\\\ &\hat \beta_{gk} | \beta_{gk} , \sigma_g^2 \sim N( \beta_{gk} , v_{gk}\sigma_g^2)\\\\ \text{Data}\\ &s_g^2\sim \sigma^2_g\frac{\chi^2_{d_g}}{d_g}\\\\ \end{array} \]

---

4.3 Limma approach

Under this assumption, it can be shown that

• Posterior Mean for the variance parameter: \[\tilde{s}^2_p = \text{E}\left[\sigma^2_p\vert s_p^2\right]=\frac{d_0 s_0^2+d_ps_p^2}{d_0+d_p}\]

• \[\tilde{T}_p=\frac{\mathbf{L}_k \hat{ \boldsymbol{\beta_p}}}{\mathbf{L}_k^T(\mathbf{X}^T\mathbf{WX})^{-1}\mathbf{L}_k^T \tilde{s}_p^2}\]

is t-distributed under \(H_0: \mathbf{L}_j\boldsymbol{\beta} = 0\)

\[\tilde{T}_p \vert H_0 \sim t(d_0 + d_p)\]

---

4.4 Empirical Bayes

• A fully Bayesian
  • would define the prior distribution by carefully choosing the prior parameters based on prior knowledge on the process
  • would confront the prior to the data and performs inference using the posterior distribution of the model parameters.
• In an empirical Bayesian approach one estimates the prior parameters based on the data.
• In Limma moment estimators for \(s_0\) and \(d_0\) are derived using the information on the gene (protein) wise variances of all genes (proteins).
• In Limma one also does not work with the full posterior distribution for the variances, but with the maximum a-posterior estimate.

---

4.5 Illustration

We borrow strength across proteins by

1. placing a scaled \(\chi^2\) prior: \(\chi^2(s_o,d_0)\) on the precisions (\(1/\sigma^2_p\))
2. estimating the prior parameters \(s_0\) and \(df_0\)
3. replacing the estimated protein-wise variances (\(s_p^2\)) with the maximum a-posteriori variance \[\tilde{s}_p = \frac{d_p s^2_p + d_0 s_0^2}{d_p+d_0}\]

sd <- sapply(
  rowData(pe[["proteinRobust"]])$msqrobModels,
  getSigma) %>%
  na.exclude
sdPost <- sapply(
  rowData(pe[["proteinRobust"]])$msqrobModels,
  getSigmaPosterior) %>%
  na.exclude

p1 <- qplot(sd,sdPost) +
  geom_abline()
p1

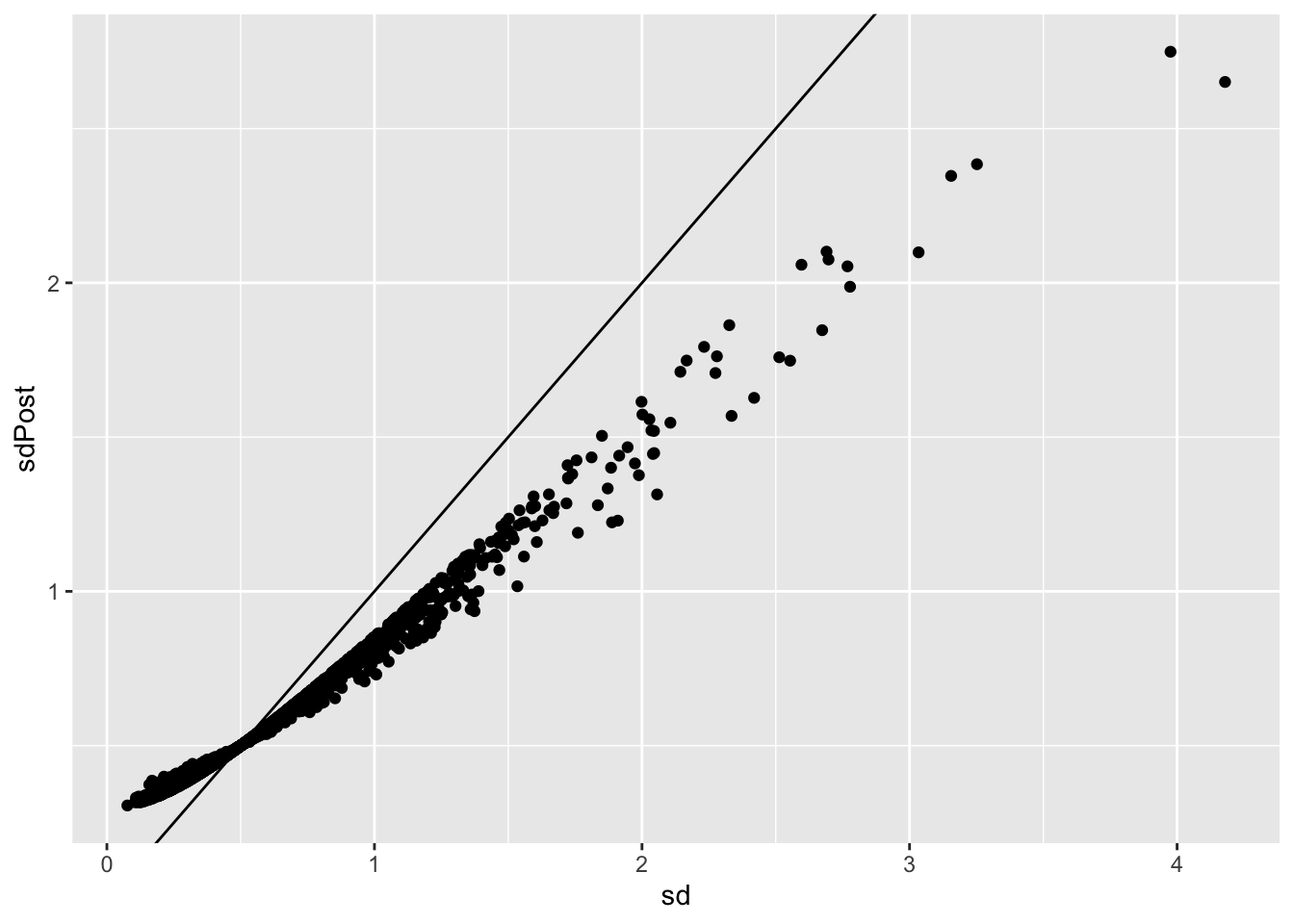
4.5.1 How do we get to the posterior standard deviation?

hlp <- limma::squeezeVar(
  var = sapply(rowData(pe[["proteinRobust"]])$msqrobModels, getVar),
  df = sapply(rowData(pe[["proteinRobust"]])$msqrobModels, getDF)
  )

4.5.1.1 Degrees of freedom of prior

hlp$df.prior

## [1] 3.385413

model <- rowData(pe[["proteinRobust"]])$msqrobModels[[2]]
getDfPosterior(model) - getDF(model)

## [1] 3.385413

4.5.1.2 posterior variance

\[\tilde s_p=\sqrt{\frac{d_p\times s^2_p + d_0 s_0^2}{d_p+d_0}} \]

hlp$var.prior

## [1] 0.2489859

varPost <- (getVar(model) * getDF(model) + hlp$df.prior * hlp$var.prior)/(getDF(model)+hlp$df.prior)
sqrt(varPost)

## [1] 0.6607153

getSigmaPosterior(model)

## [1] 0.6607153

Hence, standard deviations are shrunken towards prior standard deviation! Large standard deviations become smaller and smaller standard deviations become larger!

p1 +
  geom_hline(yintercept = hlp$var.prior^.5)

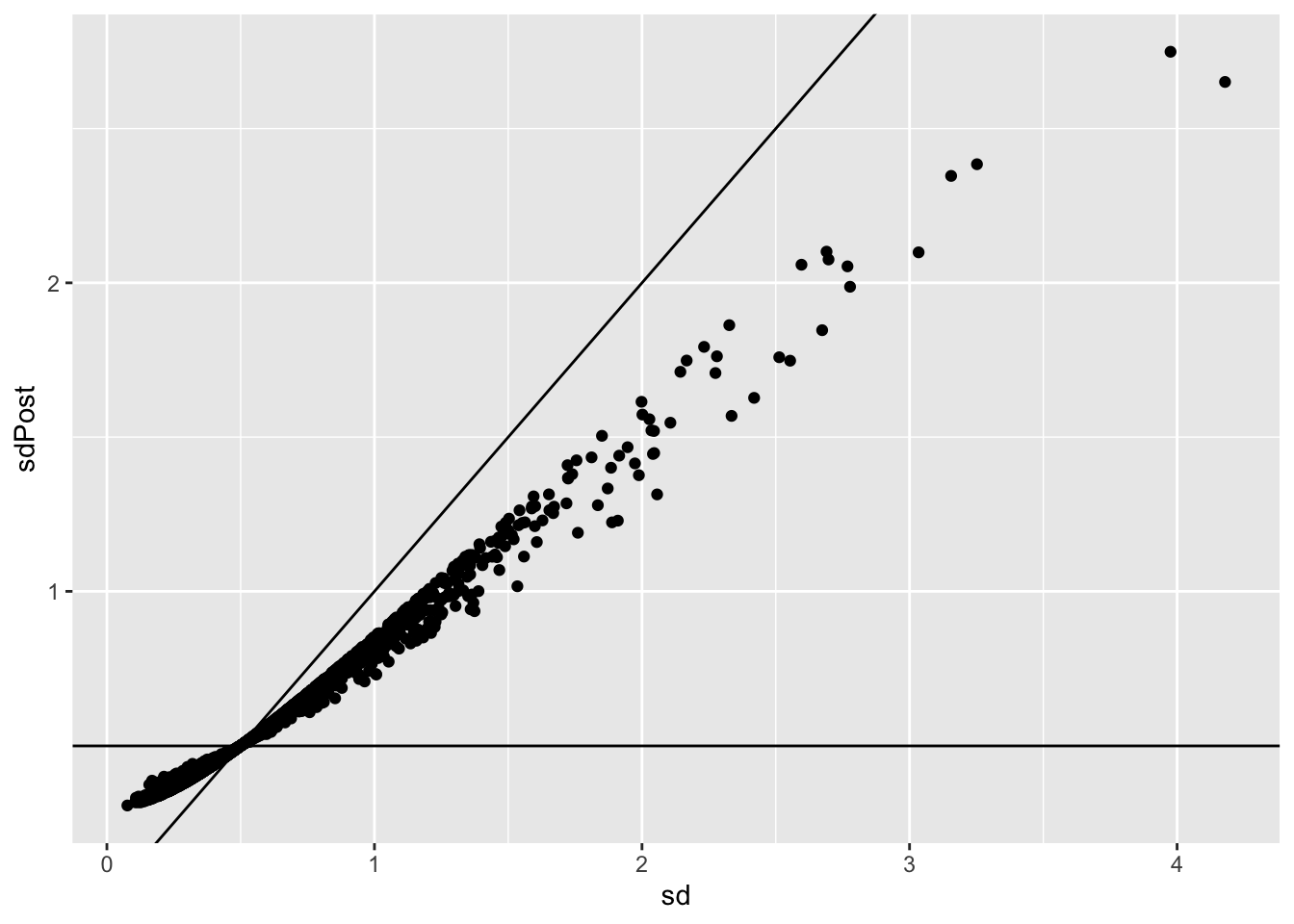
4.5.2 Illustration via Simulation

Suppose that the standard deviations for all proteins are the same and are equal to 1. We simulate proteins with the same mean as the fitted mean in the experiment but with standard deviation of 1.

nCoefs <- getCoef(rowData(pe[["proteinRobust"]])$msqrobModels[[2]]) %>% length
coefs <-
sapply(rowData(pe[["proteinRobust"]])$msqrobModels,
    function(x) getCoef(x)[1:nCoefs]
  ) %>%
  t %>%
  na.exclude


p <- nrow(coefs)
n <- ncol(pe[[1]])
f0_equalVar <- sapply(1:p,
  FUN=function(i, n, betas, sd, design) {
  rnorm(n, mean = design %*% betas[i,], sd = sd)},
  n = n,
  betas = coefs,
  sd = 1,
  design = X
  ) %>%
  t
colnames(f0_equalVar) <- colnames(pe[[1]])
sims <- readQFeatures(f0_equalVar %>% as.data.frame, ecol = 1:n, name = "sim_equalVar")
colData(sims) <- colData(pe)
sims <- msqrob(object = sims, i = "sim_equalVar", formula = ~ location*tissue + patient)

sd0 <- sapply(
  rowData(sims[["sim_equalVar"]])$msqrobModels,
  getSigma) %>%
  na.exclude
sdPost0 <- sapply(
  rowData(sims[["sim_equalVar"]])$msqrobModels,
  getSigmaPosterior) %>%
  na.exclude

qplot(sd0,sdPost0) +
  geom_abline() +
  ylim(range(sd0))

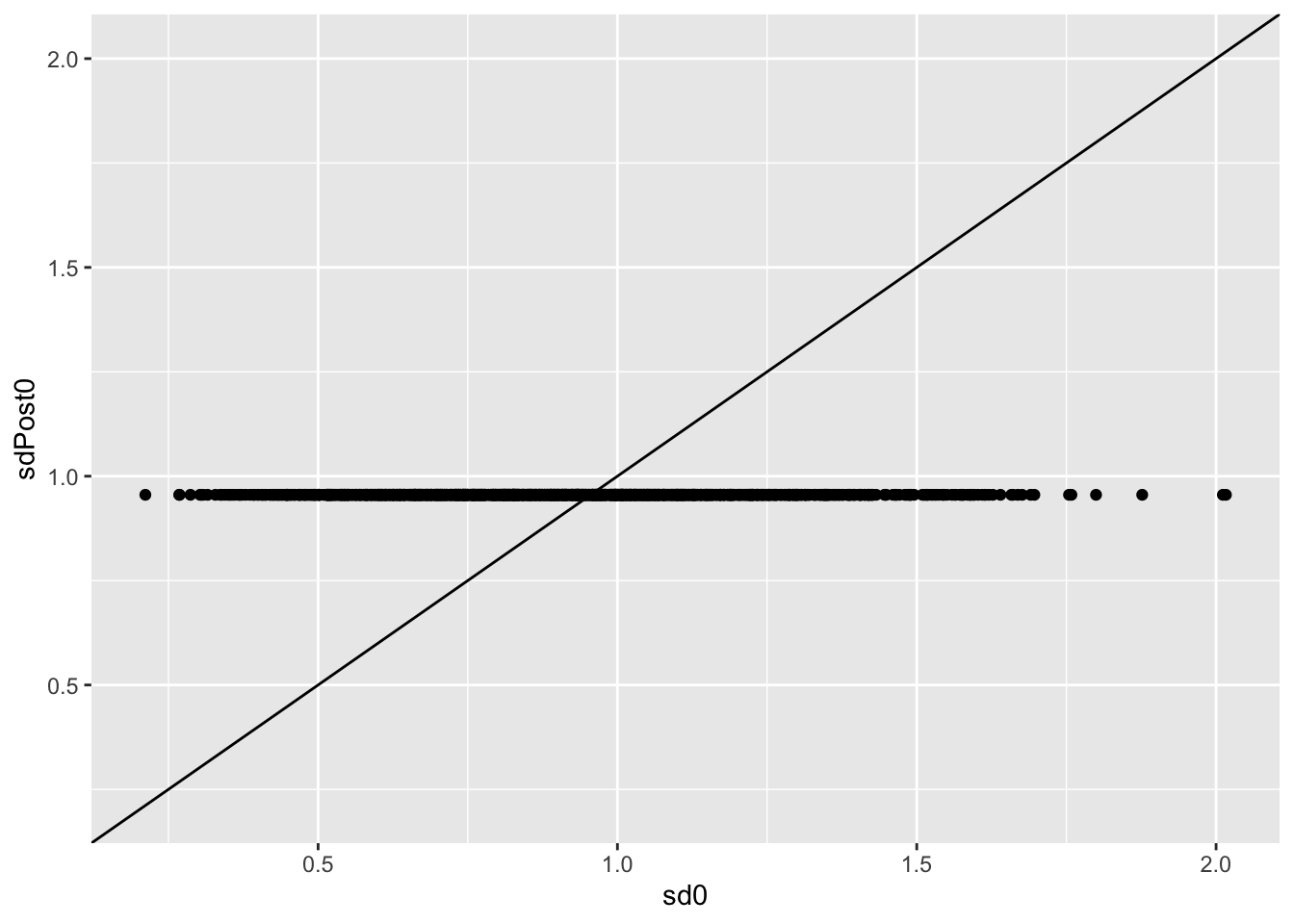
• We observe a large variability in the individual protein level standard deviation estimates.
• We simulated proteins with standard deviation of 1, but the protein estimates vary from 0.2, … , 1.93.
• Large uncertainty on the estimation of variances in small samples
• The empirical Bayes method, however, recognises that all proteins are simulated with the same variance.
• Hence, it can borrow tremendous strength across proteins to stabilize the variance estimation
• Here, it shrinks all protein variance to the prior variance, which is indeed very close to 1, the value we have adopted in the simulation.

Note, that the prior degrees of freedom are also set to infinity:

getDF(rowData(sims[["sim_equalVar"]])$msqrobModels[[1]])

## [1] 5.832087

getDfPosterior(rowData(sims[["sim_equalVar"]])$msqrobModels[[1]])

## [1] Inf

which imposes shrinkage to the prior standard deviation!

The empirical Bayes method can thus indeed recognize the common variance that is shared across all simulated proteins!

5 P-values

5.1 Simulation under H_0.

• Mean log2 protein intensity for atrium equals mean log2 protein intensity for ventriculum in the left heart region.
• sd equals the sd for the protein.

1. Extract \(\hat \sigma\) and \(\beta\)’s

sd <- sapply(
  rowData(pe[["proteinRobust"]])$msqrobModels,
  getSigma) %>%
  na.exclude

coefs <-
sapply(rowData(pe[["proteinRobust"]])$msqrobModels,
    function(x) getCoef(x)[1:nCoefs]
  ) %>%
  t %>%
  na.exclude

2. Set \(\beta_\text{tissue}\) equal to 0. No FC between atrium and ventriculum left.

coefs0 <- coefs
coefs0[,3] <- 0

3. Simulate protein expressions for each protein from a Normal distribution under \(H_0\) for left heart region (no FC between atrium and ventriculum left) and sd the sd for the protein.

set.seed(104)
f0 <- sapply(1:p,
  function(i, betas, sd, design)
  rnorm(n, mean = design %*% betas[i,], sd = sd[i]),
  betas = coefs0,
  sd = sd,
  design = X
  ) %>%
  t
colnames(f0) <- colnames(pe[[1]])

4. Setup QFeatures object and perform MSqRob analysis

sims <- readQFeatures(f0 %>% as.data.frame, ecol = 1:n, name = "sim0")
colData(sims) <- colData(pe)
sims <- msqrob(object = sims, i = "sim0", formula = ~ location*tissue + patient)
sims <- hypothesisTest(object = sims, i = "sim0", contrast = L)

5.1.1 Evaluate pvalues under H_0

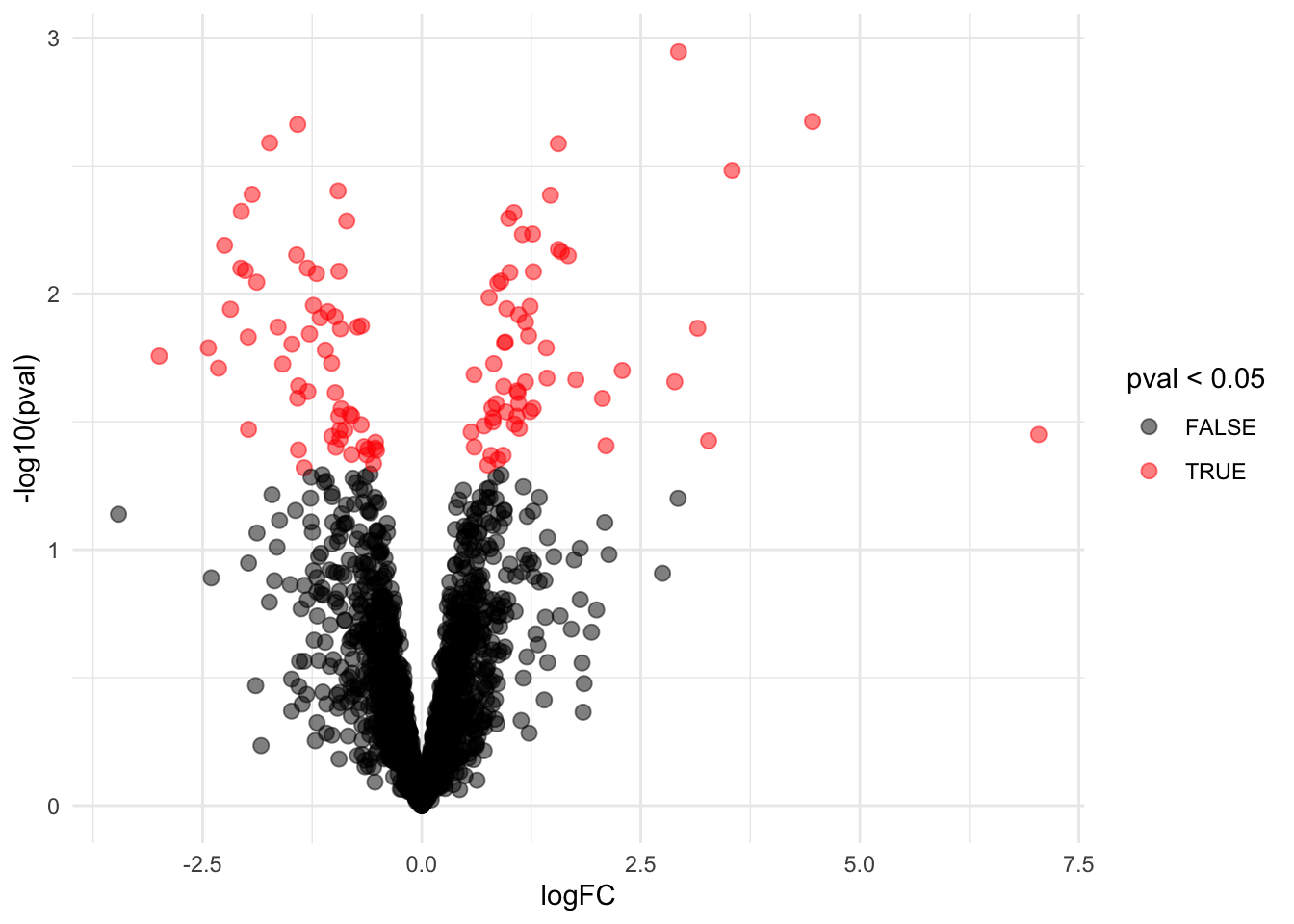
volcano <- ggplot(rowData(sims[["sim0"]])$tissueV,
                 aes(x = logFC, y = -log10(pval), color = pval < 0.05)) +
 geom_point(cex = 2.5) +
 scale_color_manual(values = alpha(c("black", "red"), 0.5)) + theme_minimal()
volcano

Number of false positives without multiple testing?

rowData(sims[["sim0"]])$tissueV %>%
  filter(pval <0.05) %>%
  nrow

## [1] 115

mean(rowData(sims[["sim0"]])$tissueV$pval < 0.05)    

## [1] 0.05665025

hist(rowData(sims[["sim0"]])$tissueV$pval,main = "simulation H0")

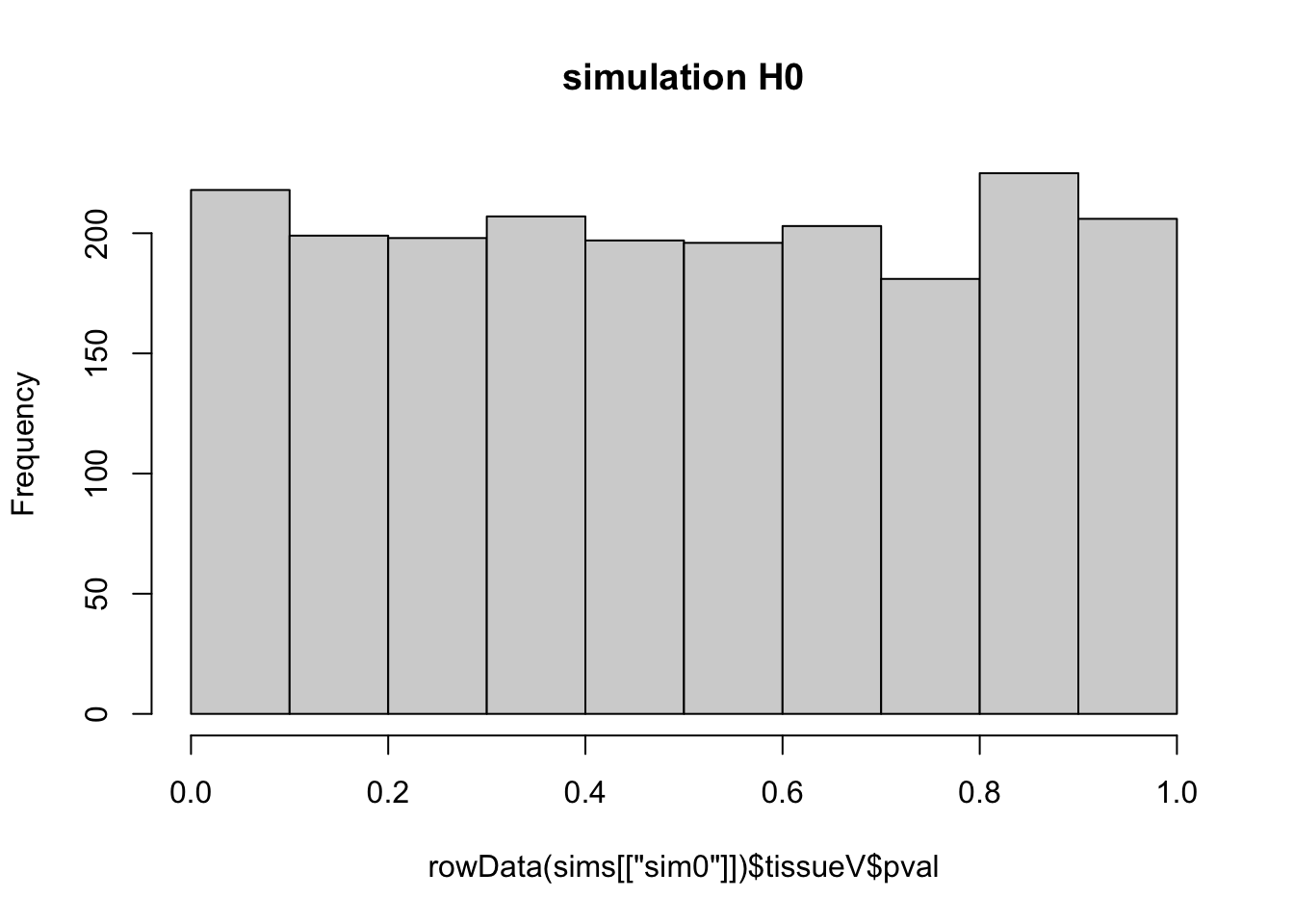
• The p-values are uniform!
• All p-values under the null are equally likely.
• Statistical hypthesis testing leads to a uniform test strategy under \(H_0\)
• If use p-value cutoff at 0.05 we expect to return 5% of the non-DE proteins as differentially expressed: many false positives can be expected!

5.2 Pvalue distribution in real experiment

hist(rowData(pe[["proteinRobust"]])$tissueV$pval, main = "realData")

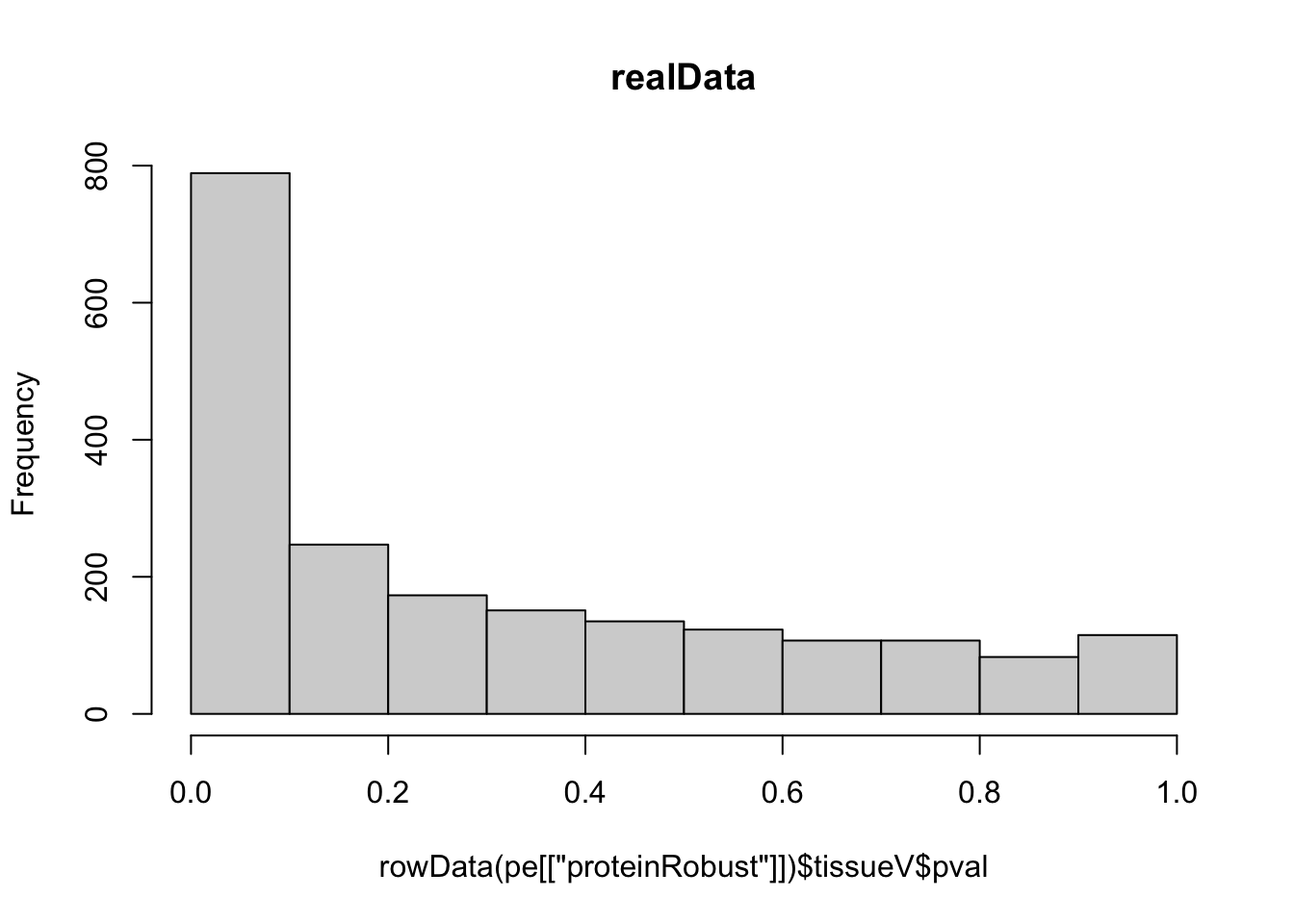
• A mixture of null proteins (non-DE): uniform, and, DE proteins: enrichment of p-values at low p-values

6 Correction for multiple testing

• We can adjust the p-values for multiple testing.

6.1 Family wise error rate correction:

• A list of returned proteins is considered to be in error as soon as it contains at most one false positive protein.

• \(\text{FWER} = P(FP \leq 1)\)

• FWER: probability of making at least one false positive decision or probability to declare at least one protein differentially abundant which is truly non differentially abundant

6.1.1 Bonferroni method

• Simple method
• \(m\) tests are performed at the level \(\alpha/m\)
• FWER\(\leq\sum\limits_{p=1}^{m}P(reject H_{0p}\vert H_{0p}\text{ is true})=m \alpha/m=\alpha\)
• Provides strong control
• Bonferroni is very conservative
• Works for dependent tests
• Adjusted p-value: \(\tilde{p}_p=\min(m\ p_p,1)\)

---

6.1.2 Bonferroni in practise

Via R functions

padj <- p.adjust(
  rowData(pe[["proteinRobust"]])$tissueV$pval,
  method = "bonferroni")

Own Implementation: adjust and make sure that p-value is smaller than 1.

m <- sum(!is.na(rowData(pe[["proteinRobust"]])$tissueV$pval))
padjSelf <-  rowData(pe[["proteinRobust"]])$tissueV$pval * m
padjSelf[padjSelf > 1] <- 1

range(padj - padjSelf, na.rm = TRUE)

## [1] 0 0

6.1.3 Illustration in simulation under \(H_0\) and heart case study

volcano <- ggplot(rowData(sims[["sim0"]])$tissueV,
                 aes(x = logFC, y = -log10(pval), color = p.adjust(pval,"bonferroni") < 0.05)) +
 geom_point(cex = 2.5) +
 scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
 theme_minimal() +
 ggtitle("simulated heart data under H0")
volcano

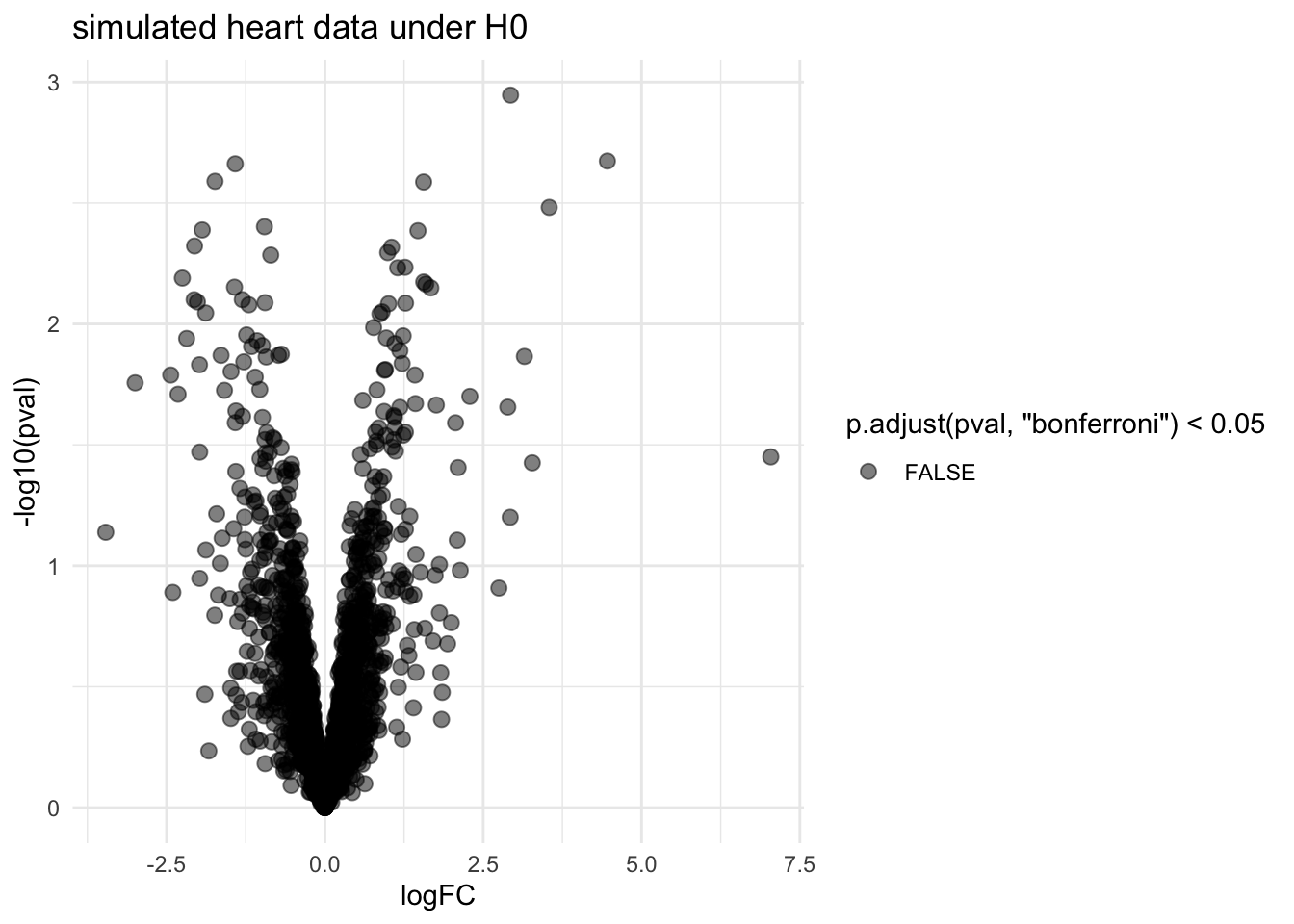
• No false positives are returned for simulation under H_0. List is correct according to FWER.

volcano <- ggplot(rowData(pe[["proteinRobust"]])$tissueV,
                 aes(x = logFC, y = -log10(pval), color = p.adjust(pval,"bonferroni") < 0.05)) +
 geom_point(cex = 2.5) +
 scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
 theme_minimal() +
 ggtitle("real heart data")
volcano

## Warning: Removed 1263 rows containing missing values or values outside the scale range
## (`geom_point()`).

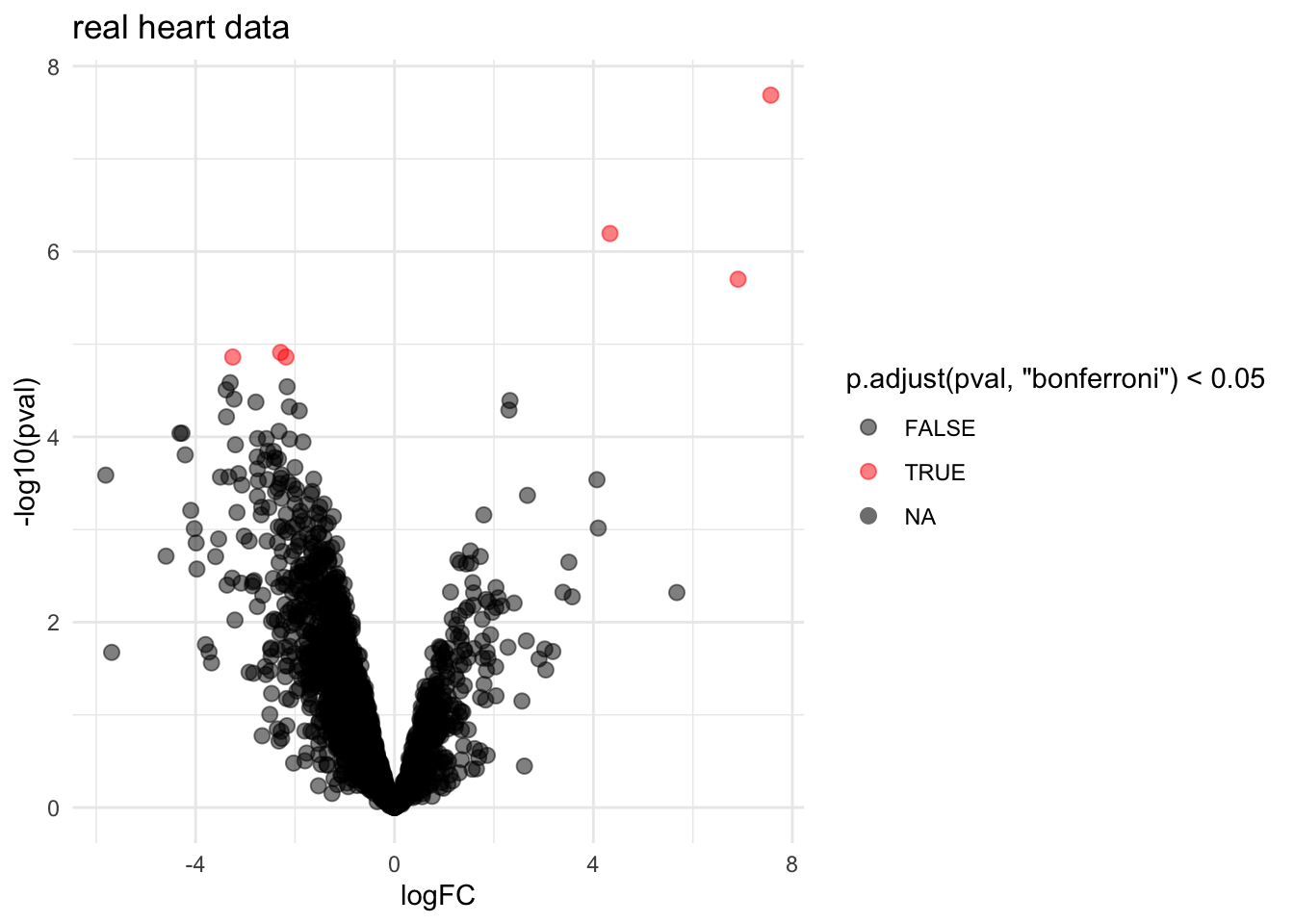
• Very few proteins are returned for real data. Very conservative!

6.2 False discovery rate

• Adjusted P-values with the Benjamini Hochberg correction correspond to the estimated FDR of the set that is returned when the significance level is set at this threshold. \[\begin{eqnarray} FDR(p_0) &=& \text{E}\left[\frac{FP}{(FP + TP)}\right]\\ &\approx&\frac{p_0 \times m}{\#p_p \leq p_0}\\ \end{eqnarray}\]

So adjusted p-value for protein j equals \[\tilde p_j = \frac{p_{0,j} \times m}{\#p_p \leq p_{0,j}}\]

However, the FDR always has to be between 0 and 1 so:

\[\tilde p_j = \min\left[\frac{p_{0,j} \times m}{\#p_p \leq p_{0,j}},1\right]\]

and the adjusted p-values should remain in the same order as the original p-values.

\[\tilde p_j = \min\limits_{\forall k: p_k > p_j} \min\left[\frac{p_{0,k} \times m}{\#p_p \leq p_{0,k}},1\right]\]

1. Order pvalues

pvals <- rowData(pe[["proteinRobust"]])$tissueV$pval
naInd <- is.na(pvals)
pHlp <- pvals[!naInd]
ord <- pHlp %>% order
pHlp <- pHlp[ord]

2. Adjust ordered p-values

pHlp <- pHlp*length(pHlp)/(1:length(pHlp))

3. Ensure adjust p-values are smaller are equal than 1

pHlp[pHlp>1] <- 1

4. Monotonicity constraint

pmin <- pHlp[length(pHlp)]
for (j in (length(pHlp)-1):1)
{
  if (pHlp[j] < pmin)
    pmin <- pHlp[j] else
    pHlp[j] <- pmin   
}

5. Put p-values back in original order

pHlp[ord] <- pHlp
pAdj <- pvals
pAdj[!naInd] <- pHlp

head(pAdj)

## [1]        NA 0.8351039        NA        NA 0.9062353        NA

head(rowData(pe[["proteinRobust"]])$tissueV)

range(rowData(pe[["proteinRobust"]])$tissueV$adjPval - pAdj,na.rm=TRUE)

## [1] -2.220446e-16  2.220446e-16

6.2.1 Illustration in simulation under \(H_0\) and heart case study

volcano <- ggplot(rowData(sims[["sim0"]])$tissueV,
                 aes(x = logFC, y = -log10(pval), color = adjPval < 0.05)) +
 geom_point(cex = 2.5) +
 scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
 theme_minimal() +
 ggtitle("simulated heart data under H0")
volcano

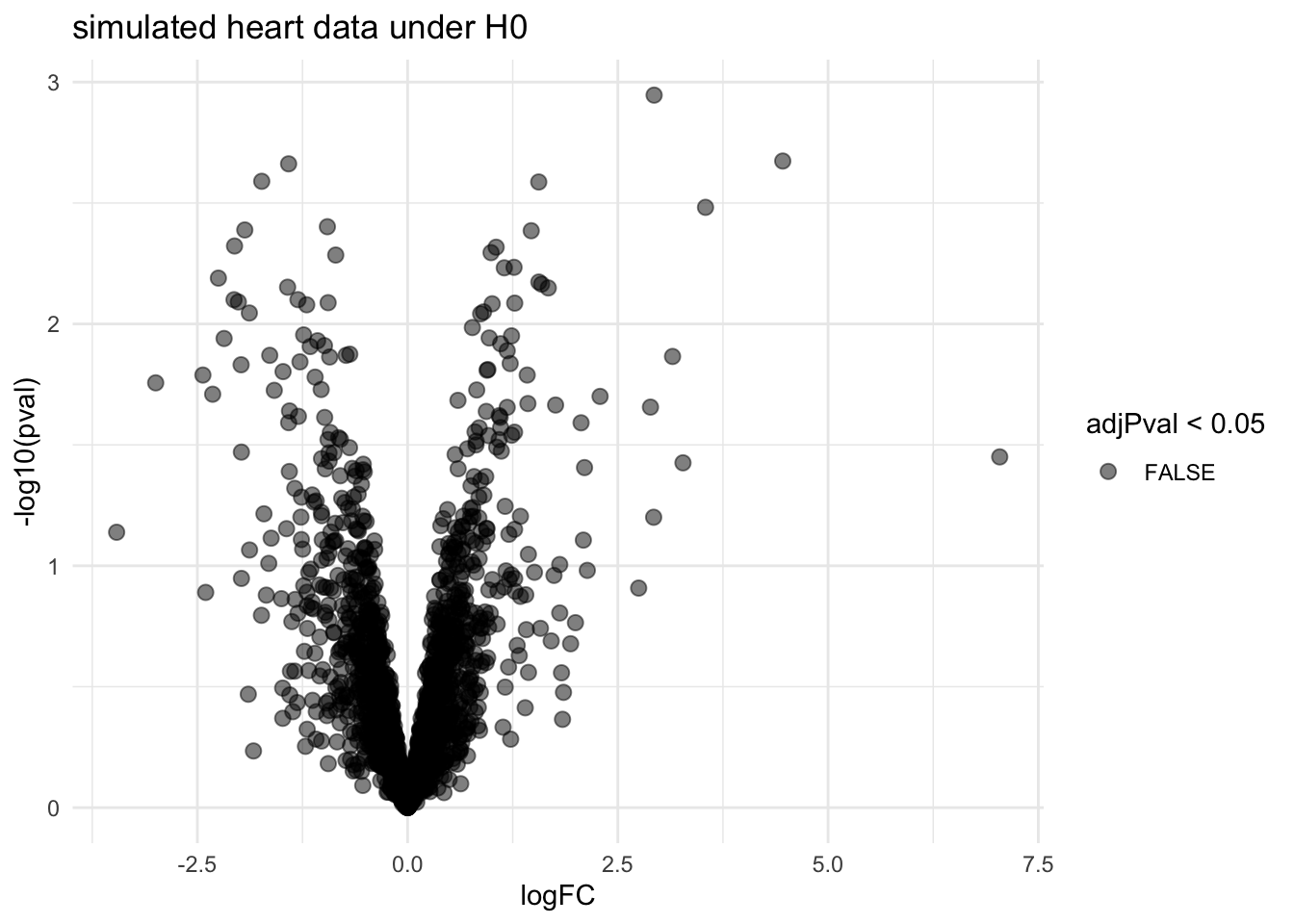
• No false positives are returned for simulation under H_0. List is correct according to FWER.
• It can be shown that the FDR-method controls the FWER when \(H_0\) is true for all features.

volcano <- ggplot(rowData(pe[["proteinRobust"]])$tissueV,
                 aes(x = logFC, y = -log10(pval), color = adjPval < 0.05)) +
 geom_point(cex = 2.5) +
 scale_color_manual(values = alpha(c("black", "red"), 0.5)) +
 theme_minimal() +
 ggtitle("real heart data")
volcano

## Warning: Removed 1263 rows containing missing values or values outside the scale range
## (`geom_point()`).

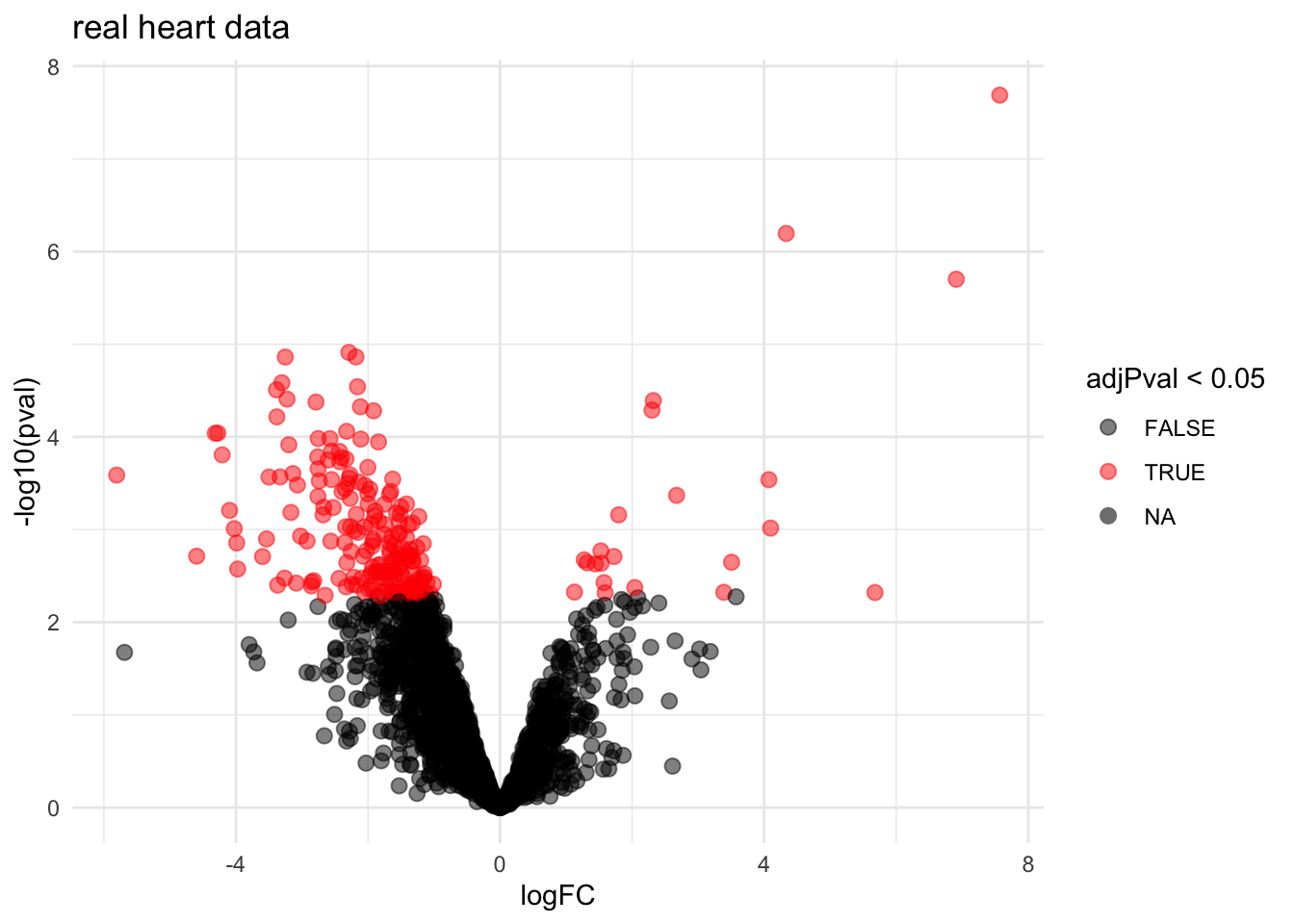
The FDR method allows us to return much longer DA protein lists at the expense of a few false positives. The FDR controls the fraction of false positives in the list that you return on average on the significance level that is adopted. So if you use \(\alpha=0.05\) we expect on average 5% of false positives in the list that we return.