Exercise 9.1: Non-parametric statistics on the shrimps dataset - solution

1 The shrimps dataset

Dataset on the accumulation of PCBs (Polychlorinated biphenyls) in the adipose tissue of shrimps. PCBs are often present in coolants, and are know to accumulate easily in the adipose tissue of shrimps. In this experiment, two groups of 18 samples (each 100 grams) of shrimps each were cultivated in different conditions, one control condition and one condition where the medium was poluted with PCBs. Note that the PCB concentrations were measured in pg/g adipose tissue.

2 Goal

The research question is; is there an effect of the growth condition on the PCB concentration in the adipose tissue of shrimps?

Load libraries:

library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

3 Import the data

shrimps <- read_tsv(
  "https://raw.githubusercontent.com/statOmics/PSLSData/main/shrimps.txt"
)

## Rows: 36 Columns: 2
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: "\t"
## dbl (2): PCB.conc, group
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

glimpse(shrimps)

## Rows: 36
## Columns: 2
## $ PCB.conc <dbl> 29.7, 24.5, 97.7, 39.1, 22.6, 32.4, 27.7, 100.1, 40.1, 23.3, …
## $ group    <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2…

4 Data tidying

shrimps <- shrimps %>%
  mutate(group = as.factor(group))

5 Data exploration

The first step is to explore the data.

shrimps %>%
  count(group)

Visualize the data:

shrimps %>%
  ggplot(aes(x = group, y = PCB.conc, fill = group)) +
  scale_fill_manual(values = c("darkorchid", "olivedrab")) +
  theme_bw() +
  geom_boxplot(outlier.shape = NA) +
  geom_jitter(width = 0.2) +
  ggtitle("Boxplot of the PCB concentrations in two groups of shrimps") +
  ylab("PCB concentration (pg/g)") +
  stat_summary(
    fun = mean, geom = "point",
    shape = 5, size = 3, color = "black",
  )

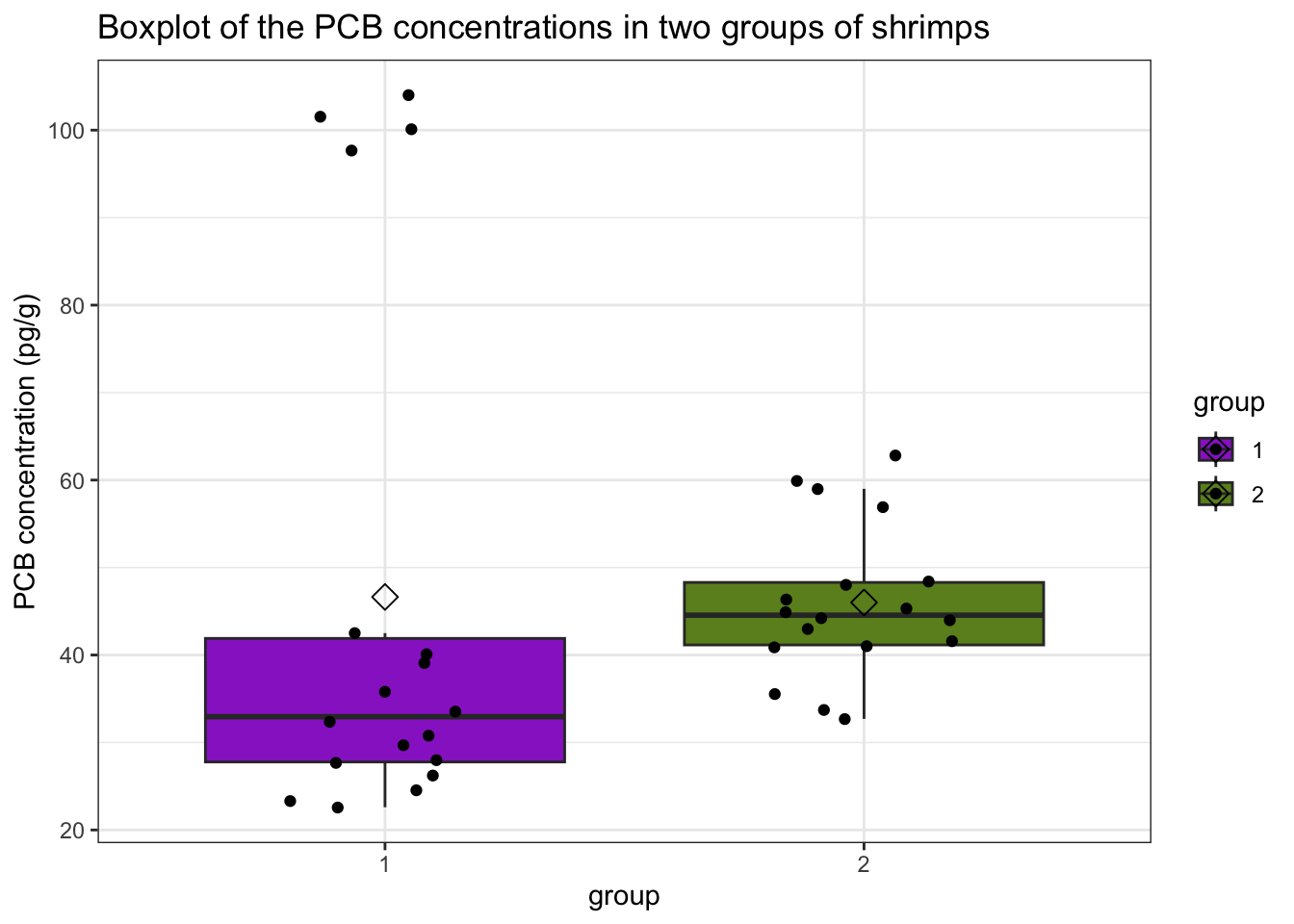
We can see that for group 1 we have four very clear outliers in the data. These values were double-checked (i.e for typing errors), but there was no reason found to believe that these values are incorrect.

6 Analysis

A good way for testing the research hypothesis is to perform an unpaired two-sample t-test to find out whether there is a significant difference in the mean PCB concentrations between both groups of samples. Before we can do this, we must check if all the required assumptions are met.

6.1 Assumptions

1. The observations are independent of each other (in both groups)
2. The data (PCB.conc) must be normally distributed (in both groups)
3. The variance is equal in the two groups.

The first assumption is met, as we randomly selected shrimps and submitted them to one of two growth conditions. No underlying correlation patterns are expected.

We can check the second assumption with a QQ-plot.

shrimps %>%
  ggplot(aes(sample = PCB.conc)) +
  geom_qq() +
  geom_qq_line() +
  facet_grid(~ group)

We clearly see that we have strong deviations from normality. Many datapoints do not lie near the quantile-quantile line. As such, we may conclude that our data are not normally distributed. In addition, the boxplots suggest that the variability differs between the two groups.

As such, we are not allowed to perform the t-test. Given the location of the outliers transformation will not help, so we will resort to non-parametric tests, i.e. to the Wilcoxon rank-sum test.

6.2 Wilcoxon rank-sum test

The Wilcoxon rank-sum test (or the Mann-Whitney U test) is an important non-parametric data analysis method. In rank-based tests, the data \(Y_i\) are first transformed to its ranked equivalent \[ R_i=R(Y_i) = \#\{Y_j: Y_j\leq Y_i; j=1,\ldots, n\}. \]

Ranks are very robust to outliers. For instance, it does not matter if the highest value in an hypothetical dataset has a value of 10 or 100; it will keep the same rank (highest rank).

Note, that there might be ties in the data, e.g., if two samples of shrimps have an equal concentration of PCBs. In this case, the Wilcoxon rank-sum test will compute mid-ranks, which are calculated as follows; \[R(Y_i) = \frac{\sum\limits_{\forall j : Y_j=Y_i}R(Y_j)}{\#{\forall j:Y_j=Y_i}} \] i.e., the midrank is equal to the mean of the ranks of equal observations.

After computing the ranks and midranks, the Wilcoxon test will compare the mean rank between both treatment groups:

wilcox_res <- wilcox.test(PCB.conc ~ group, data = shrimps)
wilcox_res

## 
##  Wilcoxon rank sum exact test
## 
## data:  PCB.conc by group
## W = 88, p-value = 0.01871
## alternative hypothesis: true location shift is not equal to 0

We find that the test is significant on the 5% significance level (p = 0.01871). The value W=88 could be calculated manually as the Mann-Withney statistic that counts how many times a value from group 1 is larger or equal than values of group 2.

6.2.1 Interpretation

The interpretation of the Wilcoxon rank-sum test is slightly more challenging than that of a t-test. Since we are no longer interpreting differences in the distributions between the groups in terms of the average differences but in in terms of the probabilistic index.

The null hypothesis of the Wilcoxon test states that the distributions are equal for both groups:

\[ H_0: f_1 = f_2 \]

In words: the distribution of PCB concentrations in shrimps are equal for both treatment conditions.

against the alternative hypothesis that

\[ H_1: P(Y_{1} \geq Y_{2}) \ne 1/2 \]

In words: The probability that a random observation of a PCB concentration derived from shrimps that was grown in the control condition is larger than or equal to than a random observation of a PCB concentration derived from a shrimps that was grown in the other condition is not equal to 50%.

We can estimate this probability based on the observed test statistic.

n1 <- n2 <- 18 # 18 observations in each group
WObs <- wilcox_res$statistic # get the observed test statistic
WObs / (n1 * n2)

##         W 
## 0.2716049

We can see that the point estimate of this probability is 27.2%.

We can interpret it as follows;

There is a probability of 27.2% that the PCB concentration in a random shrimp that was grown in the control condition is greater than or equal to the PCB concentration in a random shrimp that was grown in the treatment condition. This probability is significantly different from 50% on the 5% significance level (p = 0.01871).

---

This work is licensed under the CC BY-NC-SA 4.0 licence.