Processing math: 100%
  • 1 Randomized complete block designs
  • 2 Nature methods: Points of significance - Blocking
  • 3 Mouse example
    • 3.1 Background
    • 3.2 Data Exploration
    • 3.3 Paired Analysis
      • 3.3.1 Data exploration
    • 3.4 Randomized complete block analysis
  • 4 Power gain of an RCB vs CRD
    • 4.1 Power gain of blocking?
      • 4.1.1 Power for completely randomized design
    • 4.2 Power for randomized complete block design
    • 4.3 Impact of the amount of variability that the blocking factor explains on the power?
  • 5 Penicillin example
    • 5.1 Data
    • 5.2 Analysis
  • 6 Pseudo-replication
    • 6.1 Data exploration
    • 6.2 Wrong analysis
      • 6.2.1 No Type I error control!
  • 7 Nature methods: Split-plot designs

Creative Commons License

library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

1 Randomized complete block designs

σ2=σ2bio+σ2lab+σ2extraction+σ2run+…

  • Biological: fluctuations in protein level between mice, fluctations in protein level between cells, …
  • Technical: cage effect, lab effect, week effect, plasma extraction, MS-run, …

2 Nature methods: Points of significance - Blocking

https://www.nature.com/articles/nmeth.3005.pdf

  • Oneway anova is a special case of a completely randomized design:

    • the experimental units are sampled at random from the population
    • the treatments are randomized to the experimental units
    • Every experimental unit receives one treatment and its response variable is measured once.

  • In a block design the experimental units are blocks which are sampled at random of the population of all possible blocks.

    • The RCB restricts randomization: the treatments are randomized within the blocks.
    • it cannot be analysed using oneway anova.
    • The paired design is a special case of an RCB: block size equals 2.
    • Within block effects can be assessed using the lm function in R.

3 Mouse example

3.1 Background

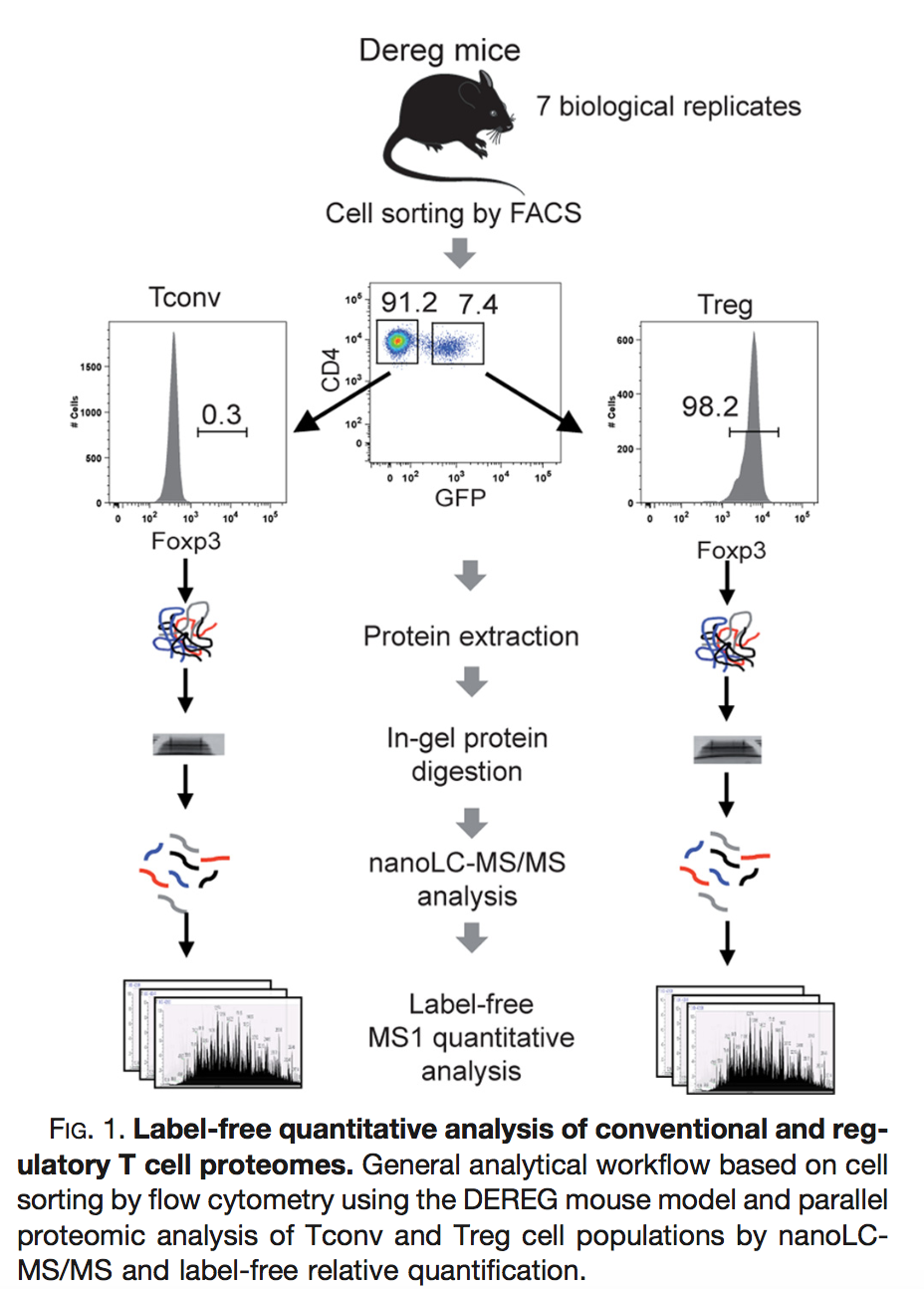
Duguet et al. (2017) MCP 16(8):1416-1432. doi: 10.1074/mcp.m116.062745

  • All treatments of interest are present within block!
  • We can estimate the effect of the treatment within block!

We focus on one protein

  • The measured intensities are already on the log2-scale. Differences between the intensities can thus be interpreted as log2 FC.
  • P16045 or Galectin-1.
  • Function: “Lectin that binds beta-galactoside and a wide array of complex carbohydrates. Plays a role in regulating apoptosis, cell proliferation and cell differentiation. Inhibits CD45 protein phosphatase activity and therefore the dephosphorylation of Lyn kinase. Strong inducer of T-cell apoptosis.” (source: uniprot)

3.2 Data Exploration

mouse <- read_tsv("https://raw.githubusercontent.com/statOmics/PSLSData/main/mouseP16045.txt")
## Rows: 14 Columns: 3
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: "\t"
## chr (2): celltype, mouse
## dbl (1): intensity
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.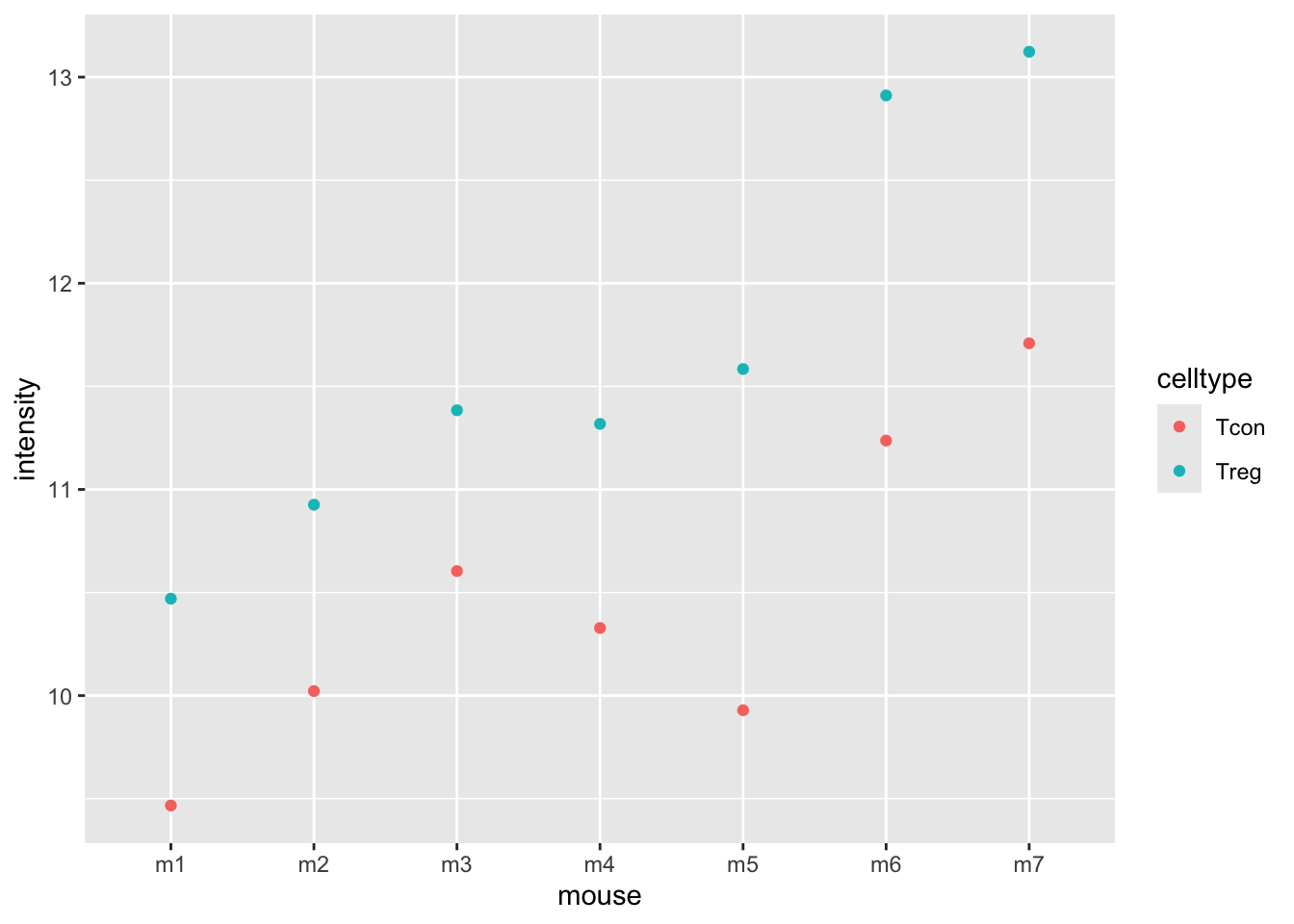
mouse
ABCDEFGHIJ0123456789
celltype
<chr>
mouse
<chr>
intensity
<dbl>
Tconm19.467
Tconm210.022
Tconm310.604
Tconm410.328
Tconm59.929
Tconm611.237
Tconm711.709
Tregm110.470
Tregm210.926
Tregm311.384
Next
12
Previous
1-10 of 14 rows
mouse %>%
  ggplot(aes(x = mouse, y = intensity, col = celltype)) +
  geom_point()

mouse %>%
  ggplot(aes(x = celltype, y = intensity)) +
  geom_point() +
  geom_line(aes(group = mouse)) +
  geom_point(aes(col = celltype))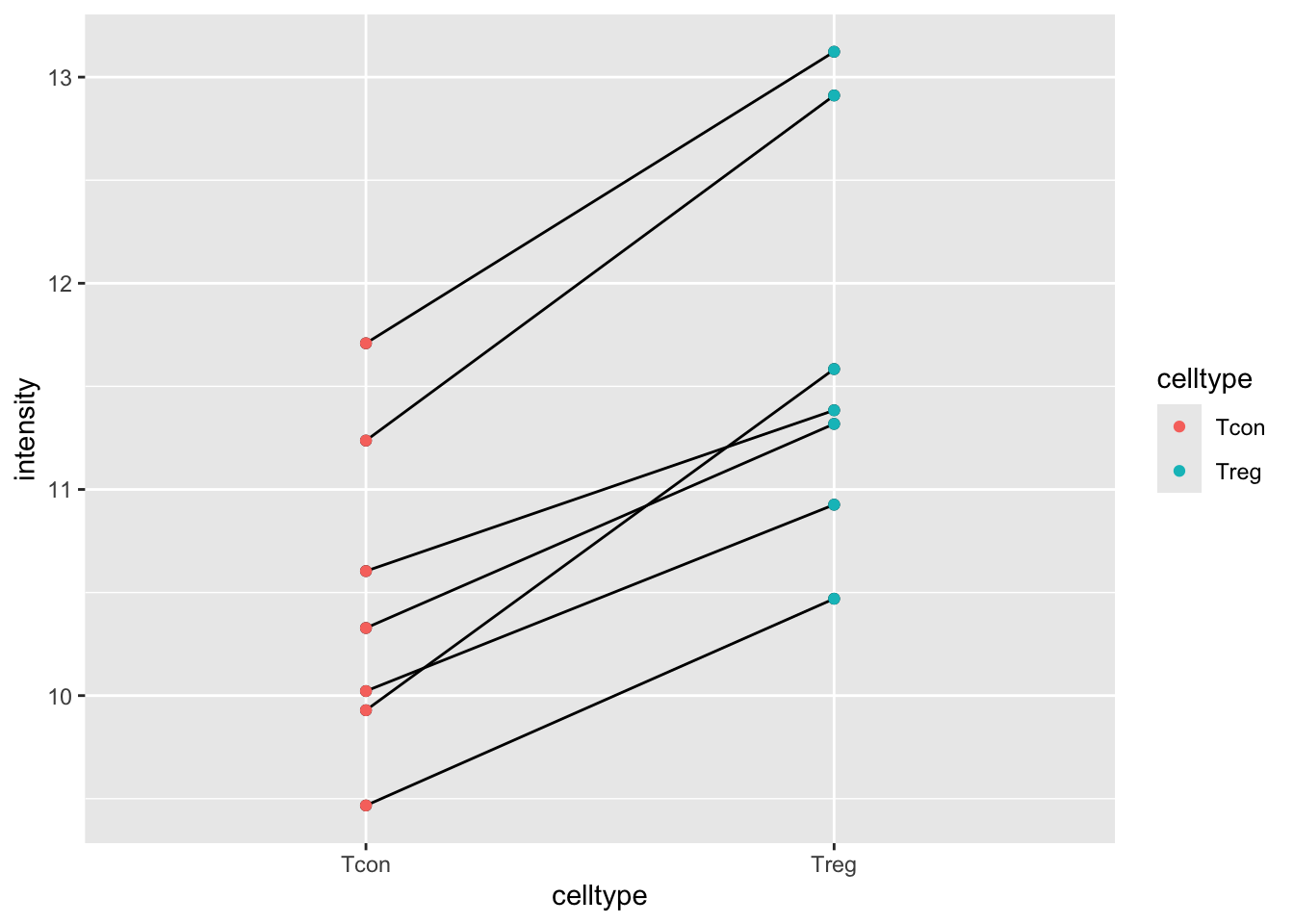

The plots show evidence for - an upregulation of the protein expression in regulatory T-cells and - a considerable variability in expression from animal to animal!

3.3 Paired Analysis

This is a paired design, which is the most simple form of randomized complete block design.

In the introduction to statistical inference we would have analyzed the data by differencing.

mouseWide <- mouse %>%
  spread(celltype, intensity) %>%
  mutate(delta = Treg - Tcon)
mouseWide
ABCDEFGHIJ0123456789
mouse
<chr>
Tcon
<dbl>
Treg
<dbl>
delta
<dbl>
m19.46710.4701.003
m210.02210.9260.904
m310.60411.3840.780
m410.32811.3180.990
m59.92911.5841.655
m611.23712.9111.674
m711.70913.1231.414
7 rows

3.3.1 Data exploration

  • Boxplot of difference
mouseWide %>%
  ggplot(aes(x = "", y = delta)) +
  geom_boxplot(outlier.shape = NA) +
  geom_jitter()

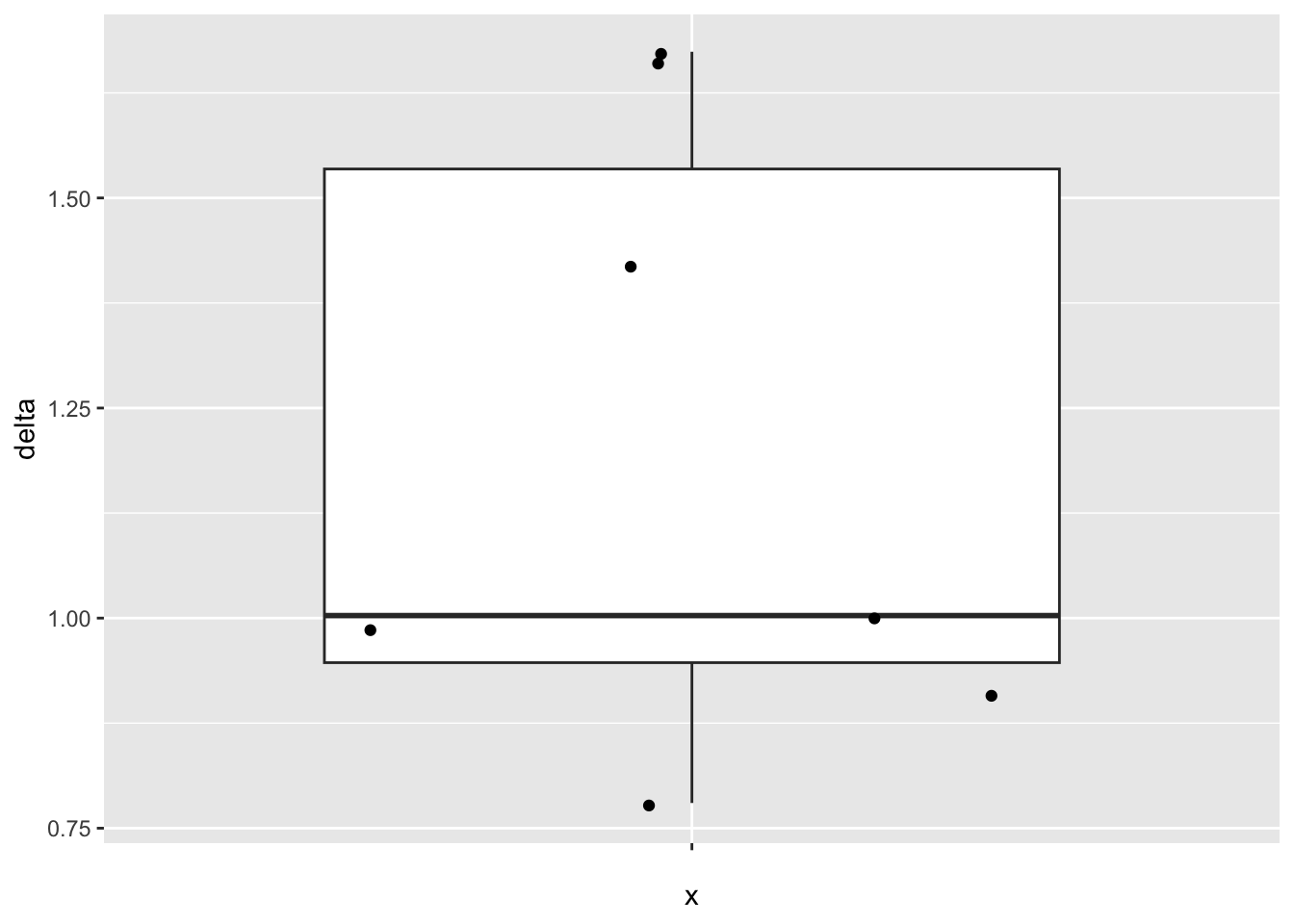
  • Summary statistics
deltaSum <- mouseWide %>%
  summarize(
      mean = mean(delta, na.rm = TRUE),
      sd = sd(delta, na.rm = TRUE),
      n = n()
  ) %>%
  mutate(se = sd / sqrt(n))
deltaSum
ABCDEFGHIJ0123456789
mean
<dbl>
sd
<dbl>
n
<int>
se
<dbl>
1.2028570.370667270.140099
1 row

Note, that the intensity data are not independent because we measured the expression in regulatory and ordinary T-cells for every animal

  • Covariance and correlation between expression in both celltypes
cor(mouseWide[, c("Tcon", "Treg")])
##         Tcon    Treg
## Tcon 1.00000 0.93874
## Treg 0.93874 1.00000
var(mouseWide[, c("Tcon", "Treg")])
##           Tcon      Treg
## Tcon 0.6101531 0.7245316
## Treg 0.7245316 0.9763042
var(mouseWide[, c("Tcon", "Treg")]) %>%
  diag() %>%
  sqrt()
##      Tcon      Treg 
## 0.7811230 0.9880811

  • There is indeed a large correlation between the expression of the protein in conventional and regulatory T-cells.

  • Standard deviation of difference?

sdxr−xc=√12ˆσ2r+(−1)2ˆσ2c+2×1×−1׈σr,c=√ˆσ2r+ˆσ2c−2׈σr,c

sdDelta2 <- (c(-1, 1) %*% var(mouseWide[, c("Tcon", "Treg")]) %*% c(-1, 1)) %>%
  sqrt()
sdDelta2
##           [,1]
## [1,] 0.3706672
seDeltaBar <- sdDelta2 / sqrt(deltaSum$n)
seDeltaBar
##          [,1]
## [1,] 0.140099
deltaSum
ABCDEFGHIJ0123456789
mean
<dbl>
sd
<dbl>
n
<int>
se
<dbl>
1.2028570.370667270.140099
1 row
  • The standard deviation on the difference is much lower because of the strong correlation!
  • Note, that the paired design enabled us to estimate the difference in log2-expression between the two cell types in every animal (log2 FC).
t.test(delta~1, mouseWide)
## 
##  One Sample t-test
## 
## data:  delta
## t = 8.5858, df = 6, p-value = 0.0001372
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  0.8600472 1.5456671
## sample estimates:
## mean of x 
##  1.202857

3.4 Randomized complete block analysis

We can also analyse the design using a linear model, i.e. with

  • a main effect for cell type and
  • a main effect for the block factor mouse

Because we have measured the two cell types in every mouse, we can thus estimate the average log2-intensity of the protein in the T-cells for each mouse.

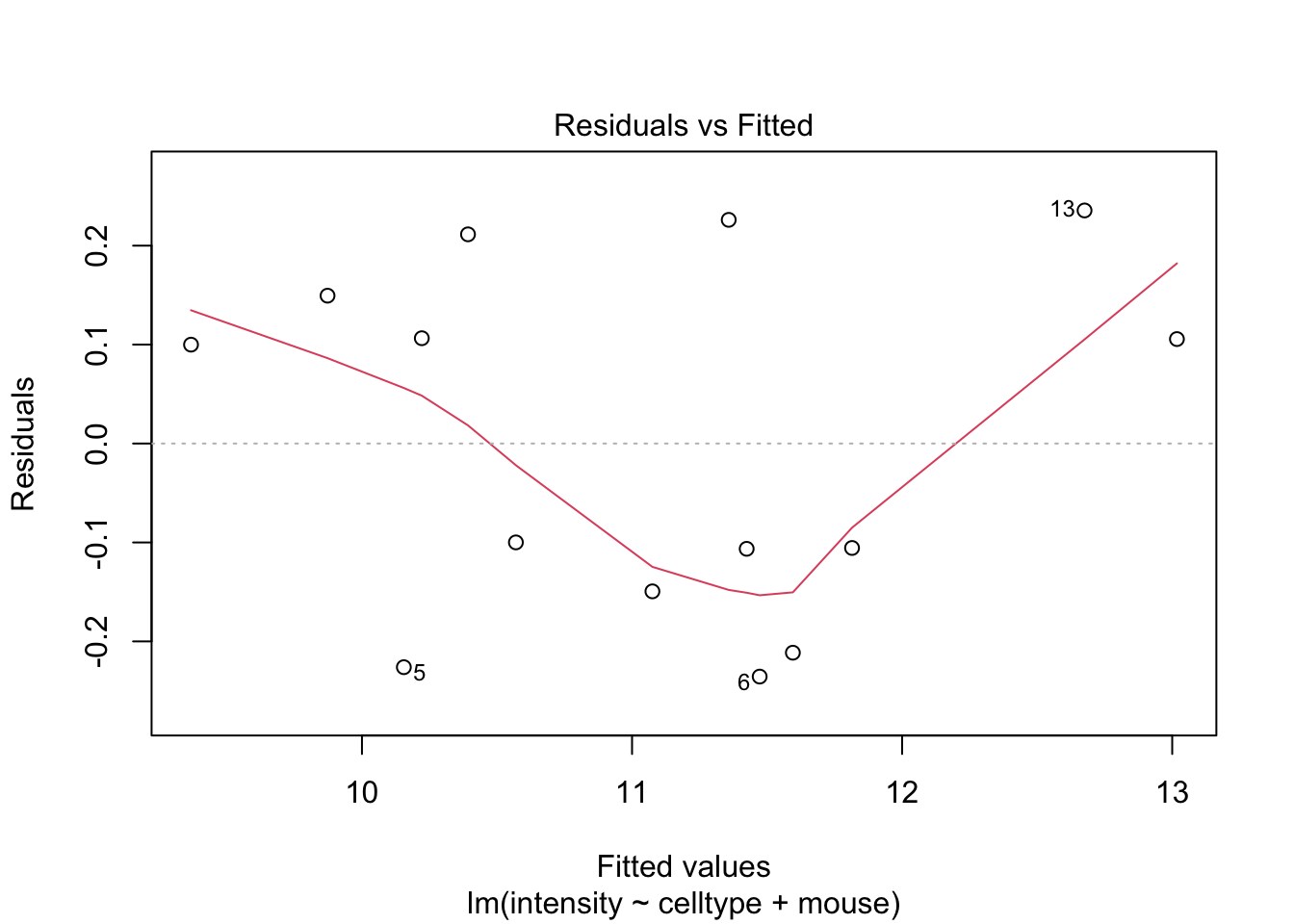
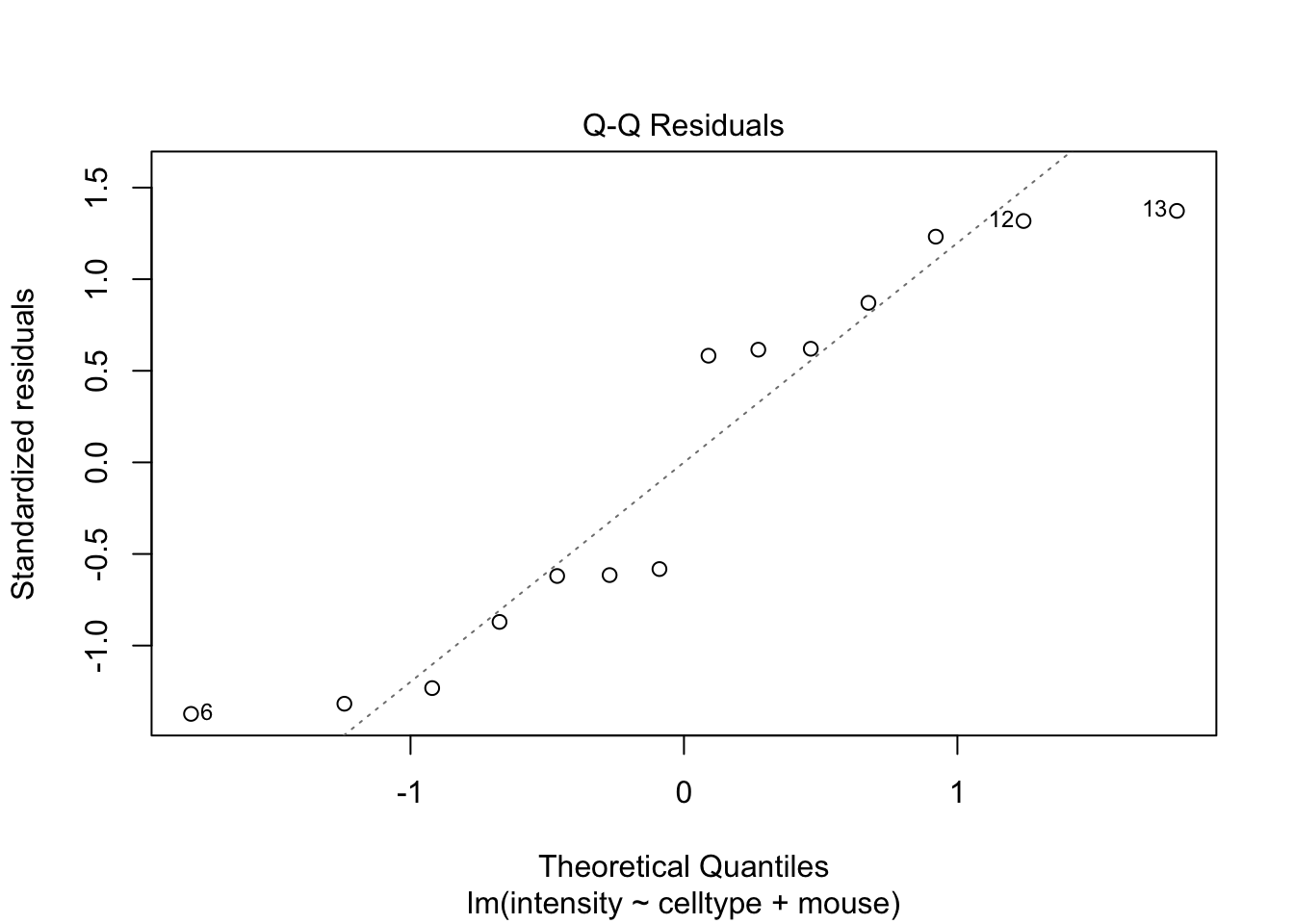
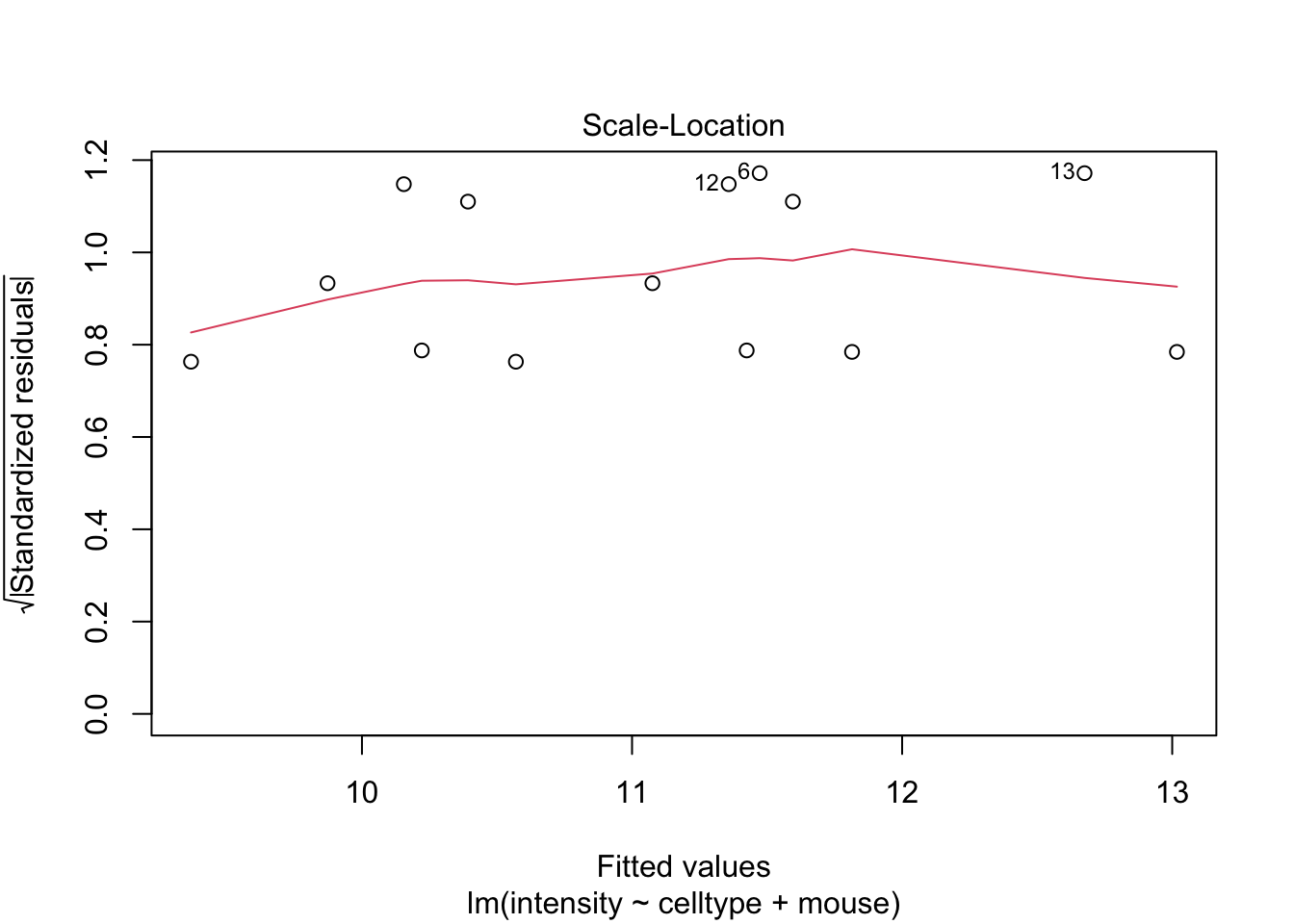
lmRCB <- lm(intensity ~ celltype + mouse, mouse)
plot(lmRCB, which = c(1, 2, 3))

If you have doubts on that your data violates the assumptions you can always simulate data from a model with similar effects as yours but where are distributional assumptions hold and compare the residual plots.

design <- model.matrix(intensity ~ celltype + mouse, mouse)
sigmaMouse <- sqrt(car::Anova(lmRCB, type = "III")["mouse", "Sum Sq"] / car::Anova(lmRCB, type = "III")["mouse", "Df"])
betas <- lmRCB$coefficients
nMouse <- mouse$mouse %>%
  unique() %>%
  length()

par(mfrow = c(3, 3))
for (i in 1:9)
{
  mouseEffect <- rnorm(nMouse, sd = sigmaMouse)
  betasMouse <- mouseEffect[-1] - mouseEffect[1]
  betas[-c(1:2)] <- betasMouse
  ysim <- design %*% betas + rnorm(nrow(design), sd = sigma(lmRCB))
  plot(lm(ysim ~ -1 + design), which = 1)
}

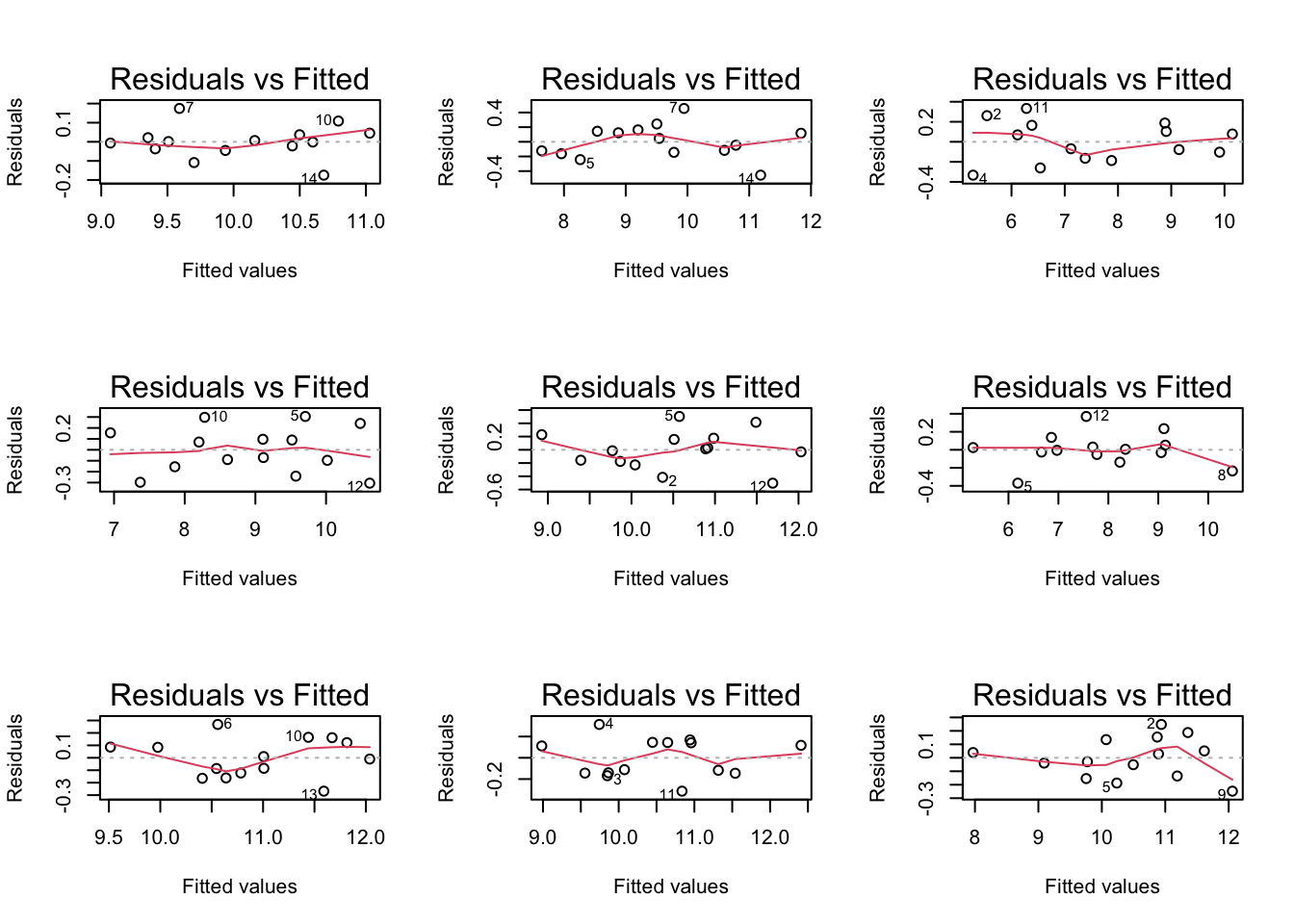
The deviations seen in our plot are in line with what those observed in simulations under the model assumptions. Hence, we can use the model for statistical inference.

anovaRCB <- car::Anova(lmRCB, type = "III")
summary(lmRCB)
## 
## Call:
## lm(formula = intensity ~ celltype + mouse, data = mouse)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.2356 -0.1387  0.0000  0.1387  0.2356 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    9.3671     0.1981  47.277 6.00e-09 ***
## celltypeTreg   1.2029     0.1401   8.586 0.000137 ***
## mousem2        0.5055     0.2621   1.929 0.102036    
## mousem3        1.0255     0.2621   3.913 0.007869 ** 
## mousem4        0.8545     0.2621   3.260 0.017245 *  
## mousem5        0.7880     0.2621   3.006 0.023809 *  
## mousem6        2.1055     0.2621   8.033 0.000199 ***
## mousem7        2.4475     0.2621   9.338 8.55e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2621 on 6 degrees of freedom
## Multiple R-squared:  0.9717, Adjusted R-squared:  0.9388 
## F-statistic: 29.47 on 7 and 6 DF,  p-value: 0.000309
t.test(delta ~1 , mouseWide)
## 
##  One Sample t-test
## 
## data:  delta
## t = 8.5858, df = 6, p-value = 0.0001372
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  0.8600472 1.5456671
## sample estimates:
## mean of x 
##  1.202857
anovaRCB
ABCDEFGHIJ0123456789
 
 
Sum Sq
<dbl>
Df
<dbl>
F value
<dbl>
Pr(>F)
<dbl>
(Intercept)153.548547512235.154206.002402e-09
celltype5.0640286173.715351.371937e-04
mouse9.1065619622.093527.601249e-04
Residuals0.41218246NANA
4 rows

Notice that

  1. the estimate, se, t-test statistic and p-value for the celltype effect of interest is the same as in the paired t-test!

  2. the anova analysis shows that we model the total variability in the protein expression in T-cells using variability due to the cell type (CT), the variability from mouse to mouse (M) and residual variability (R) within mouse that we cannot explain. Indeed,

SSTot=SSCT+SSM+SSE14.6=5.1+9.1+0.4

So the celltype and the mouse effect explain respectively SSCTSSTot×100SSMSSTot×10034.762.4

percent of the variability in the protein expression values and SSESSTot×100=2.8 percent cannot be explained.

Note, that

  • the variability from mouse to mouse is the largest source of variability in the model,
  • This variability can be estimated with the RCB design and
  • can thus be isolated from the residual variability
  • leading to a much higher precision on the estimate of the average log2 FC between regulatory and conventional T-cells that what would be obtained with a CRD!

Note, that the RCB also has to sacrifice a number of degrees of freedom to estimate the mouse effect, here 6 DF.

Hence, the power gain of the RCB is a trade-off between the variability that can be explained by the block effect and the loss in DF.

→ We were able to isolate the variance in expression between animals/blocks from our analysis!

→ This reduces the variance of the residuals and leads to a power gain if the variability between mice/blocks is large.

Also note that,

ˆσ2=SSEn−p=SSTot−SSM−SSCTn−p

  • Hence, blocking is beneficial if the reduction in sum of squares of the residuals is large compared to the degrees of freedom that are sacrificed.
  • Thus if SSM can explain a large part of the total variability.

Further, the degrees of freedom affect the t-distribution that is used for inference, which has broader tails if the residual degrees of freedom n−p are getting smaller.

4 Power gain of an RCB vs CRD

In this section we will subset the original data in two experiments:

  • A randomized complete block design with three mice
  • A completely randomized design with six mice but where we only measure one cell type in each mouse.
set.seed(859)
mRcb <- mouse %>%
  pull(mouse) %>%
  unique() %>%
  sample(size = 3)

rcbSmall <- mouse %>% filter(mouse %in% mRcb)
rcbSmall
ABCDEFGHIJ0123456789
celltype
<chr>
mouse
<chr>
intensity
<dbl>
Tconm210.022
Tconm310.604
Tconm711.709
Tregm210.926
Tregm311.384
Tregm713.123
6 rows
mCrd <- mouse %>%
  pull(mouse) %>%
  unique() %>%
  sample(size = 6)


crdSmall <-
  bind_rows(
    mouse %>%
      filter(mouse %in% mCrd[1:3]) %>%
      filter(celltype == "Tcon"),
    mouse %>%
      filter(mouse %in% mCrd[-(1:3)]) %>%
      filter(celltype == "Treg")
  )
crdSmall
ABCDEFGHIJ0123456789
celltype
<chr>
mouse
<chr>
intensity
<dbl>
Tconm210.022
Tconm410.328
Tconm611.237
Tregm110.470
Tregm311.384
Tregm713.123
6 rows

So in both experiments we need to do six mass spectrometry runs.

lmCRDSmall <- lm(intensity ~ celltype, crdSmall)
summary(lmCRDSmall)
## 
## Call:
## lm(formula = intensity ~ celltype, data = crdSmall)
## 
## Residuals:
##      1      2      3      4      5      6 
## -0.507 -0.201  0.708 -1.189 -0.275  1.464 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   10.5290     0.6077  17.326 6.51e-05 ***
## celltypeTreg   1.1300     0.8594   1.315    0.259    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.053 on 4 degrees of freedom
## Multiple R-squared:  0.3018, Adjusted R-squared:  0.1272 
## F-statistic: 1.729 on 1 and 4 DF,  p-value: 0.2589
anova(lmCRDSmall)
ABCDEFGHIJ0123456789
 
 
Df
<int>
Sum Sq
<dbl>
Mean Sq
<dbl>
F value
<dbl>
Pr(>F)
<dbl>
celltype11.9153501.9153501.7289060.2588669
Residuals44.4313561.107839NANA
2 rows
lmRCBSmall <- lm(intensity ~ celltype + mouse, rcbSmall)
anova(lmRCBSmall)
ABCDEFGHIJ0123456789
 
 
Df
<int>
Sum Sq
<dbl>
Mean Sq
<dbl>
F value
<dbl>
Pr(>F)
<dbl>
celltype11.59960071.5996006728.335250.03352697
mouse24.04256532.0212826735.804910.02717029
Residuals20.11290530.05645267NANA
3 rows
summary(lmRCBSmall)
## 
## Call:
## lm(formula = intensity ~ celltype + mouse, data = rcbSmall)
## 
## Residuals:
##        1        2        3        4        5        6 
##  0.06433  0.12633 -0.19067 -0.06433 -0.12633  0.19067 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    9.9577     0.1940  51.329 0.000379 ***
## celltypeTreg   1.0327     0.1940   5.323 0.033527 *  
## mousem3        0.5200     0.2376   2.189 0.160094    
## mousem7        1.9420     0.2376   8.173 0.014641 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2376 on 2 degrees of freedom
## Multiple R-squared:  0.9804, Adjusted R-squared:  0.951 
## F-statistic: 33.32 on 3 and 2 DF,  p-value: 0.02928

Note, that

  • we are able to pick up the upregulation between regulatory T-cells and ordinary T-cells with the RCB but not with the CRD.
  • the standard error of the log2FCTreg-Tcon estimate is a factor 4.4 smaller for the RCB design!

A poor data analysis who forgets about the blocking will be back at square one:

wrongRbc <- lm(intensity ~ celltype, rcbSmall)
anova(wrongRbc)
ABCDEFGHIJ0123456789
 
 
Df
<int>
Sum Sq
<dbl>
Mean Sq
<dbl>
F value
<dbl>
Pr(>F)
<dbl>
celltype11.5996011.5996011.5397540.2824583
Residuals44.1554711.038868NANA
2 rows
summary(wrongRbc)
## 
## Call:
## lm(formula = intensity ~ celltype, data = rcbSmall)
## 
## Residuals:
##       1       2       3       4       5       6 
## -0.7563 -0.1743  0.9307 -0.8850 -0.4270  1.3120 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   10.7783     0.5885  18.316 5.23e-05 ***
## celltypeTreg   1.0327     0.8322   1.241    0.282    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.019 on 4 degrees of freedom
## Multiple R-squared:  0.2779, Adjusted R-squared:  0.09743 
## F-statistic:  1.54 on 1 and 4 DF,  p-value: 0.2825

So, the block to block variability is then absorbed in the variance estimator of the residual.

Of course, we are never allowed to analyse an RCB with a model for a CRD (without block factor) because blocking imposes a randomization restriction: we randomize the treatment within block.

4.1 Power gain of blocking?

4.1.1 Power for completely randomized design

varBetweenPlusWithin <- sum(car::Anova(lmRCB, type = "III")[c("mouse", "Residuals"), "Sum Sq"]) / sum(car::Anova(lmRCB, type = "III")[c("mouse", "Residuals"), "Df"])

alpha <- 0.05
nSim <- 20000
b0 <- 0
sd <- sqrt(varBetweenPlusWithin)
ns <- c(3, 7)
deltas <- lmRCB$coefficients["celltypeTreg"]

L <- limma::makeContrasts("celltypeTreg", levels = c("(Intercept)", "celltypeTreg"))
## Warning in limma::makeContrasts("celltypeTreg", levels = c("(Intercept)", :
## Renaming (Intercept) to Intercept
powerFast <- matrix(NA, nrow = length(ns) * length(deltas), ncol = 3) %>% as.data.frame()
names(powerFast) <- c("b1", "n", "power")

i <- 0
for (n in ns)
{
  n1 <- n2 <- n

  ### Simulation
  predictorData <- data.frame(celltype = rep(c("Tcon", "Treg"), c(n1, n2)) %>% as.factor())
  design <- model.matrix(~celltype, predictorData)

  for (b1 in deltas)
  {
    ySim <- rnorm(nrow(predictorData) * nSim, sd = sd)
    dim(ySim) <- c(nrow(predictorData), nSim)
    ySim <- ySim + c(design %*% c(b0, b1))
    ySim <- t(ySim)

    ### Fitting
    fitAll <- limma::lmFit(ySim, design)

    ### Inference
    varUnscaled <- c(t(L) %*% fitAll$cov.coefficients %*% L)
    contrasts <- fitAll$coefficients %*% L
    seContrasts <- varUnscaled^.5 * fitAll$sigma
    tstats <- contrasts / seContrasts
    pvals <- pt(abs(tstats), fitAll$df.residual, lower.tail = FALSE) * 2

    i <- i + 1
    powerFast[i, ] <- c(b1, n, mean(pvals < alpha))
  }
}
powerFast
ABCDEFGHIJ0123456789
b1
<dbl>
n
<dbl>
power
<dbl>
1.20285730.24675
1.20285770.64355
2 rows

Because we have a simple 2 group comparison we can also calculate the power using the power.t.test function.

power.t.test(n = 3, delta = lmRCB$coefficients["celltypeTreg"], sd = sqrt(varBetweenPlusWithin))
## 
##      Two-sample t test power calculation 
## 
##               n = 3
##           delta = 1.202857
##              sd = 0.8906339
##       sig.level = 0.05
##           power = 0.2477638
##     alternative = two.sided
## 
## NOTE: n is number in *each* group
power.t.test(n = 7, delta = lmRCB$coefficients["celltypeTreg"], sd = sqrt(varBetweenPlusWithin))
## 
##      Two-sample t test power calculation 
## 
##               n = 7
##           delta = 1.202857
##              sd = 0.8906339
##       sig.level = 0.05
##           power = 0.6411438
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

4.2 Power for randomized complete block design

alpha <- 0.05
nSim <- 20000
b0 <- 0
sd <- sigma(lmRCB)
sdMouse <- sqrt(car::Anova(lmRCB)["mouse", "Sum Sq"] / car::Anova(lmRCB)["mouse", "Df"])
ns <- c(3, 7)
deltas <- lmRCB$coefficients["celltypeTreg"]


powerFastBlocking <- matrix(NA, nrow = length(ns) * length(deltas), ncol = 3) %>% as.data.frame()
names(powerFastBlocking) <- c("b1", "n", "power")

i <- 0
for (n in ns)
{

  ### Simulation
  predictorData <- data.frame(celltype = rep(c("Tcon", "Treg"), each = n) %>% as.factor(), mouse = paste0("m", rep(1:n, 2)))
  design <- model.matrix(~ celltype + mouse, predictorData)
  L <- limma::makeContrasts("celltypeTreg", levels = colnames(design))

  for (b1 in deltas)
  {
    ySim <- rnorm(nrow(predictorData) * nSim, sd = sd)
    dim(ySim) <- c(nrow(predictorData), nSim)
    mouseEffect <- rnorm(n, sd = sdMouse)
    betasMouse <- mouseEffect[-1] - mouseEffect[1]
    ySim <- ySim + c(design %*% c(b0, b1, betasMouse))
    ySim <- t(ySim)

    ### Fitting
    fitAll <- limma::lmFit(ySim, design)

    ### Inference
    varUnscaled <- c(t(L) %*% fitAll$cov.coefficients %*% L)
    contrasts <- fitAll$coefficients %*% L
    seContrasts <- varUnscaled^.5 * fitAll$sigma
    tstats <- contrasts / seContrasts
    pvals <- pt(abs(tstats), fitAll$df.residual, lower.tail = FALSE) * 2

    i <- i + 1
    powerFastBlocking[i, ] <- c(b1, n, mean(pvals < alpha))
  }
}
## Warning in limma::makeContrasts("celltypeTreg", levels = colnames(design)):
## Renaming (Intercept) to Intercept
## Warning in limma::makeContrasts("celltypeTreg", levels = colnames(design)):
## Renaming (Intercept) to Intercept
powerFastBlocking
ABCDEFGHIJ0123456789
b1
<dbl>
n
<dbl>
power
<dbl>
1.20285730.79505
1.20285771.00000
2 rows

Note, that the power is indeed much larger for the randomized complete block design. Both for the designs with 6 and 14 mass spectrometer runs.

Because we have an RCB with a block size of 2 (paired design) we can also calculate the power using the power.t.test function with type = "one.sample" and sd equal to the standard deviation of the difference.

power.t.test(n = 3, delta = mean(mouseWide$delta), sd = sd(mouseWide$delta))
## 
##      Two-sample t test power calculation 
## 
##               n = 3
##           delta = 1.202857
##              sd = 0.3706672
##       sig.level = 0.05
##           power = 0.8389961
##     alternative = two.sided
## 
## NOTE: n is number in *each* group
power.t.test(n = 7, delta = mean(mouseWide$delta), sd = sd(mouseWide$delta))
## 
##      Two-sample t test power calculation 
## 
##               n = 7
##           delta = 1.202857
##              sd = 0.3706672
##       sig.level = 0.05
##           power = 0.999826
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Note, that the power is slightly different because for the power.t.test function we conditioned on the mice from our study. While in the simulation study we generated data for new mice by simulating the mouse effect from a normal distribution.

4.3 Impact of the amount of variability that the blocking factor explains on the power?

We will vary the block effect explains σ2betweenσ2between+σ2within=1−σ2withinσ2between+σ2within So in our example that is the ratio between the variability between the mice and the sum of the variability between and within the mice. Note, that the within mouse variability was the variance of the errors of the RCB. The ratio for our experiment equals

varBetweenPlusWithin <- sum(car::Anova(lmRCB, type = "III")[c("mouse", "Residuals"), "Sum Sq"]) / sum(car::Anova(lmRCB, type = "III")[c("mouse", "Residuals"), "Df"])
varWithin <- car::Anova(lmRCB)["Residuals", "Sum Sq"] / car::Anova(lmRCB)["Residuals", "Df"]
varBetweenPlusWithin
## [1] 0.7932287
varWithin
## [1] 0.06869707
1 - varWithin / varBetweenPlusWithin
## [1] 0.9133956
alpha <- 0.05
nSim <- 20000
b0 <- 0
varBetweenPlusWithin <- sum(car::Anova(lmRCB, type = "III")[c("mouse", "Residuals"), "Sum Sq"]) / sum(car::Anova(lmRCB, type = "III")[c("mouse", "Residuals"), "Df"])


ns <- c(3, 7)
deltas <- lmRCB$coefficients["celltypeTreg"]

fracVars <- seq(0, .95, .05)

powerFastBlockingLow <- matrix(NA, nrow = length(ns) * length(fracVars), ncol = 3) %>% as.data.frame()
names(powerFastBlockingLow) <- c("fracVars", "n", "power")

i <- 0


for (n in ns)
{

  ### Simulation
  predictorData <- data.frame(celltype = rep(c("Tcon", "Treg"), each = n) %>% as.factor(), mouse = paste0("m", rep(1:n, 2)))
  design <- model.matrix(~ celltype + mouse, predictorData)
  L <- limma::makeContrasts("celltypeTreg", levels = colnames(design))
  for (fracVar in fracVars)
  {
    sd <- sqrt(varBetweenPlusWithin * (1 - fracVar))
    sdMouse <- sqrt(varBetweenPlusWithin * fracVar)
    for (b1 in deltas)
    {
      ySim <- rnorm(nrow(predictorData) * nSim, sd = sd)
      dim(ySim) <- c(nrow(predictorData), nSim)
      mouseEffect <- rnorm(n, sd = sdMouse)
      betasMouse <- mouseEffect[-1] - mouseEffect[1]
      ySim <- ySim + c(design %*% c(b0, b1, betasMouse))
      ySim <- t(ySim)

      ### Fitting
      fitAll <- limma::lmFit(ySim, design)

      ### Inference
      varUnscaled <- c(t(L) %*% fitAll$cov.coefficients %*% L)
      contrasts <- fitAll$coefficients %*% L
      seContrasts <- varUnscaled^.5 * fitAll$sigma
      tstats <- contrasts / seContrasts
      pvals <- pt(abs(tstats), fitAll$df.residual, lower.tail = FALSE) * 2

      i <- i + 1
      powerFastBlockingLow[i, ] <- c(fracVar, n, mean(pvals < alpha))
    }
  }
}
## Warning in limma::makeContrasts("celltypeTreg", levels = colnames(design)):
## Renaming (Intercept) to Intercept
## Warning in limma::makeContrasts("celltypeTreg", levels = colnames(design)):
## Renaming (Intercept) to Intercept
powerFastBlockingLow
ABCDEFGHIJ0123456789
fracVars
<dbl>
n
<dbl>
power
<dbl>
0.0030.16935
0.0530.17575
0.1030.18705
0.1530.19050
0.2030.19445
0.2530.20330
0.3030.20745
0.3530.22805
0.4030.24110
0.4530.26075
Next
1234
Previous
1-10 of 40 rows
gg_color_hue <- function(n) {
  hues <- seq(15, 375, length = n + 1)
  hcl(h = hues, l = 65, c = 100)[1:n]
}
cols <- gg_color_hue(2)

powerFastBlockingLow %>%
  as.data.frame() %>%
  mutate(n = as.factor(n)) %>%
  ggplot(aes(fracVars, power, group = n, color = n)) +
  geom_line() +
  geom_hline(yintercept = powerFast %>% filter(n == 3) %>% pull(power), color = cols[1]) +
  annotate("text",
    label = "CRD (n=3)",
    x = 0.05, y = powerFast %>% filter(n == 3) %>% pull(power) + .02, size = 3, colour = cols[1]
  ) +
  geom_hline(yintercept = powerFast %>% filter(n == 7) %>% pull(power), color = cols[2]) +
  annotate("text",
    label = "CRD (n=7)",
    x = 0.05, y = powerFast %>% filter(n == 7) %>% pull(power) + .02, size = 3, colour = cols[2]
  ) +
  xlab(expression(~ sigma[between]^2 / (sigma[between]^2 + sigma[within]^2))) +
  geom_vline(xintercept = 1 - varWithin / varBetweenPlusWithin) +
  xlim(0, 1)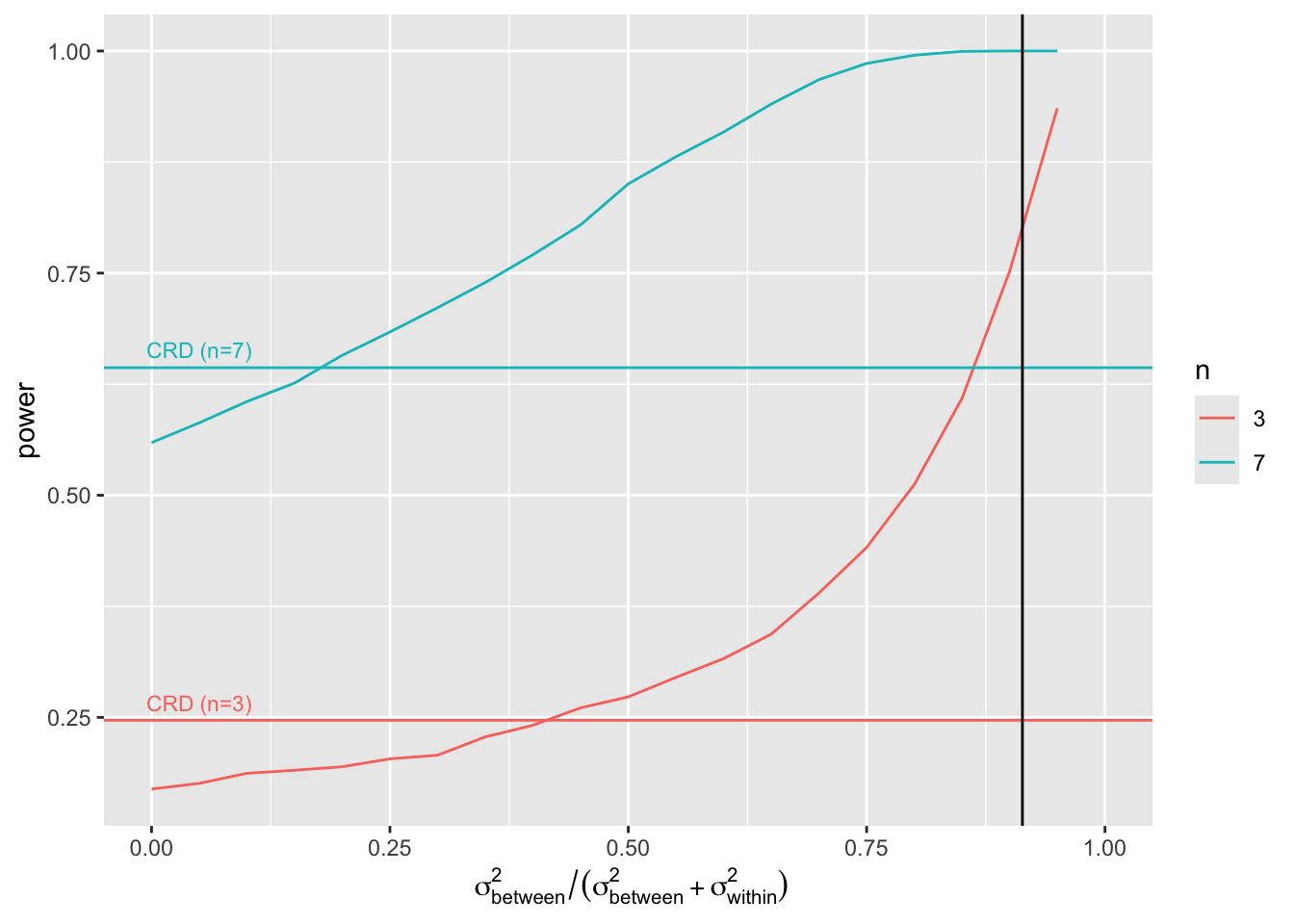

  • So if the variance that is explained by the block effect is small you will loose power as compared to the analysis with a CRD design. Indeed, then

    • SSE does not reduce much and
    • nblocks-1 degrees of freedom have been sacrificed.

  • As soon as the block effect explains a large part of the variability it is very beneficial to use a randomized complete block design!

  • Note, that the same number of mass spectrometry runs have to be done for both the RCB and CRD design. However, for the RCB we only need half of the mice.

5 Penicillin example

The production of penicillin corn steep liquor is used. Corn steep liquor is produced in blends and there is a considerable variability between the blends. Suppose that

  • four competing methods have to be evaluated to produce penicillin (A-D),
  • one blends is sufficient for four runs of a penicillin batch reactor and
  • the 20 runs can be scheduled for the experiment.

How would you assign the methods to the blends.

data(penicillin, package = "faraway")
table(penicillin$blend, penicillin$treat)
##         
##          A B C D
##   Blend1 1 1 1 1
##   Blend2 1 1 1 1
##   Blend3 1 1 1 1
##   Blend4 1 1 1 1
##   Blend5 1 1 1 1

5.1 Data

head(penicillin)
ABCDEFGHIJ0123456789
 
 
treat
<fct>
blend
<fct>
yield
<dbl>
1ABlend189
2BBlend188
3CBlend197
4DBlend194
5ABlend284
6BBlend277
6 rows
matrix(penicillin$yield, nrow = 5, ncol = 4, byrow = TRUE, dimnames = list(levels(penicillin$blend), levels(penicillin$treat)))
##         A  B  C  D
## Blend1 89 88 97 94
## Blend2 84 77 92 79
## Blend3 81 87 87 85
## Blend4 87 92 89 84
## Blend5 79 81 80 88
penicillin %>%
  ggplot(aes(x = blend, y = yield, group = treat, color = treat)) +
  geom_line() +
  geom_point()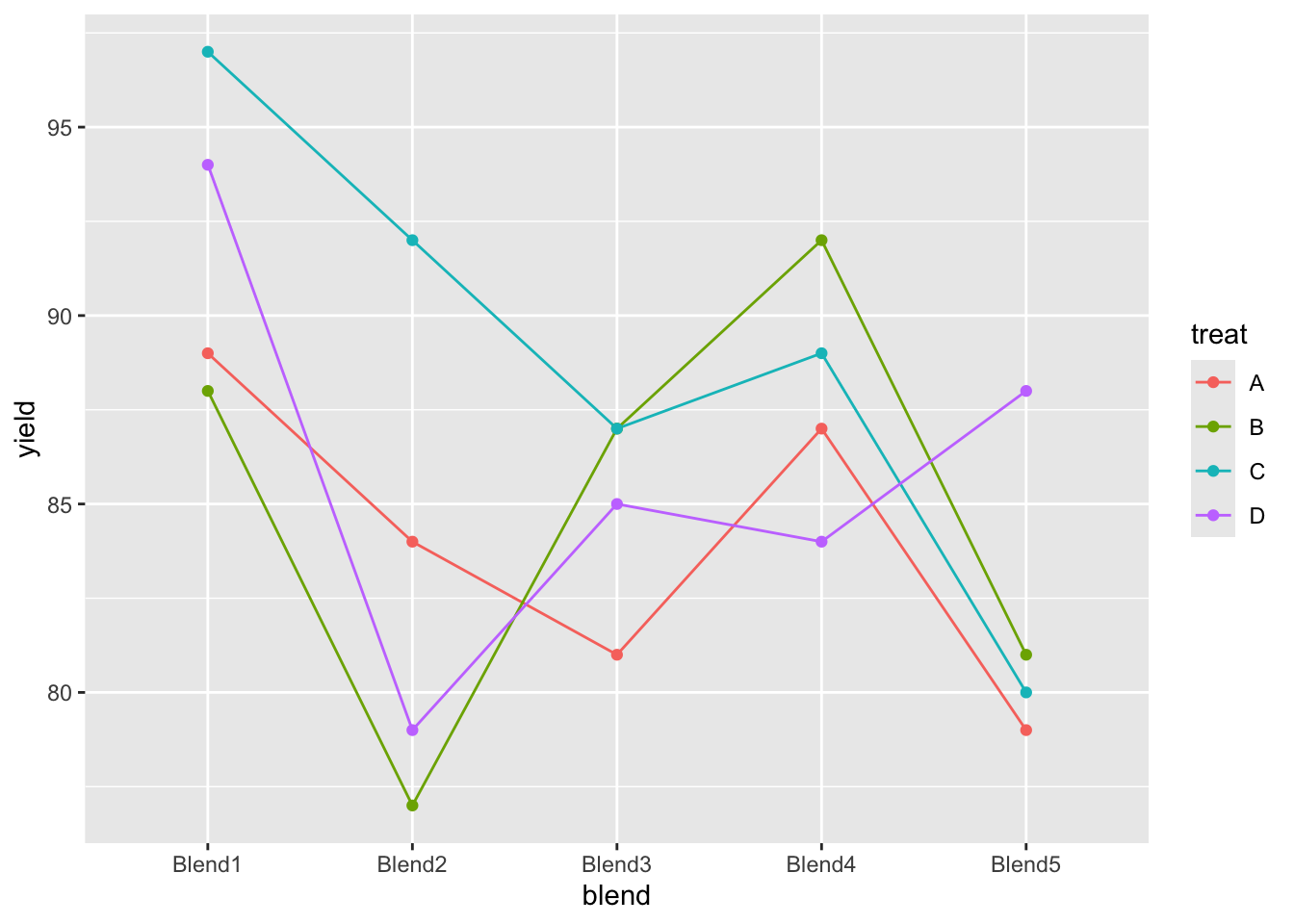

penicillin %>%
  ggplot(aes(x = treat, y = yield, group = blend, color = blend)) +
  geom_line() +
  geom_point()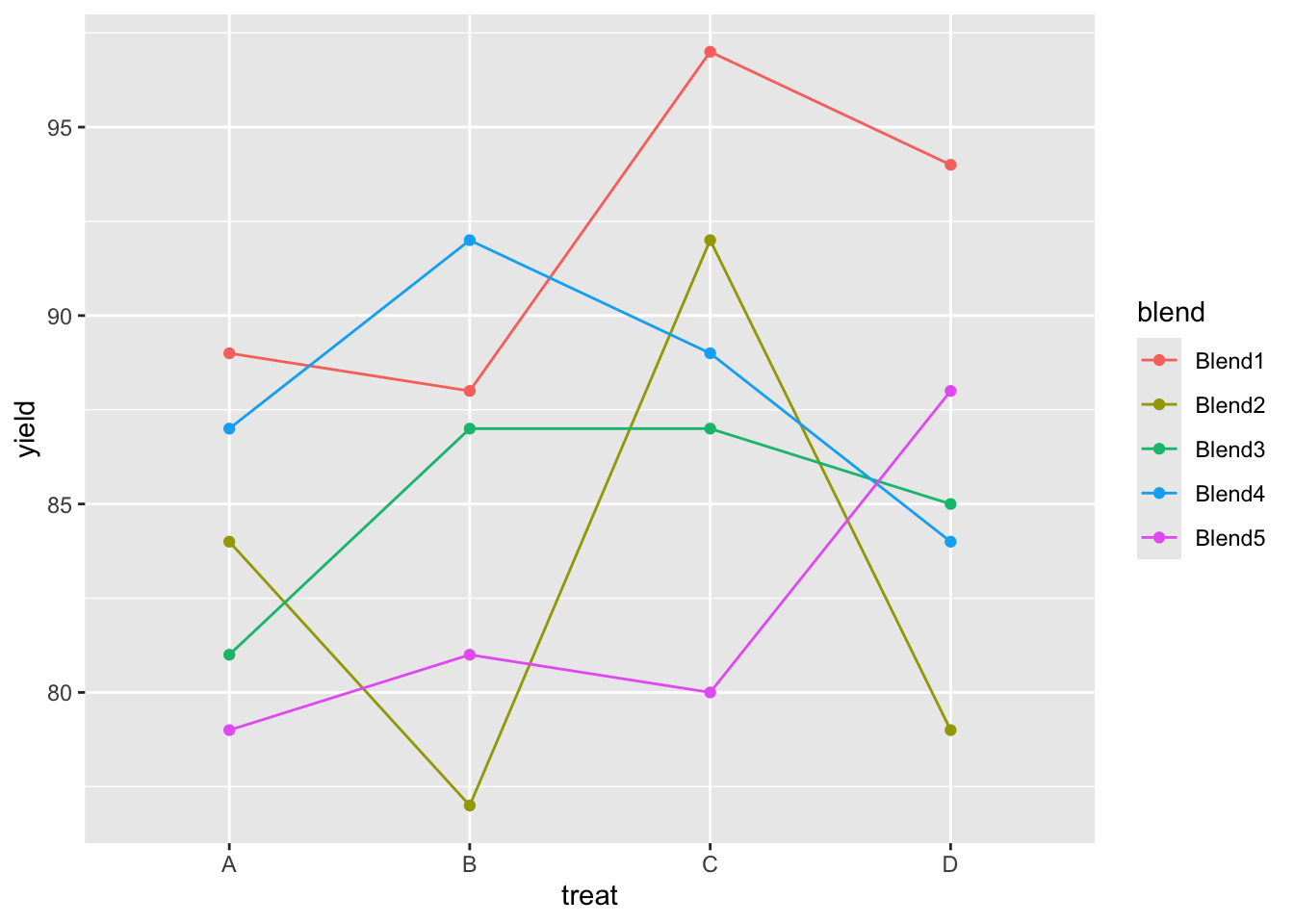

5.2 Analysis

We analyse the yield using

  • a factor for blend and
  • a factor for treatment.
lmPen <- lm(yield ~ treat + blend, data = penicillin)
plot(lmPen)

car::Anova(lmPen, type = "III")
ABCDEFGHIJ0123456789
 
 
Sum Sq
<dbl>
Df
<dbl>
F value
<dbl>
Pr(>F)
<dbl>
(Intercept)2025011075.2212394.097853e-13
treat7031.2389383.386581e-01
blend26443.5044254.074617e-02
Residuals22612NANA
4 rows

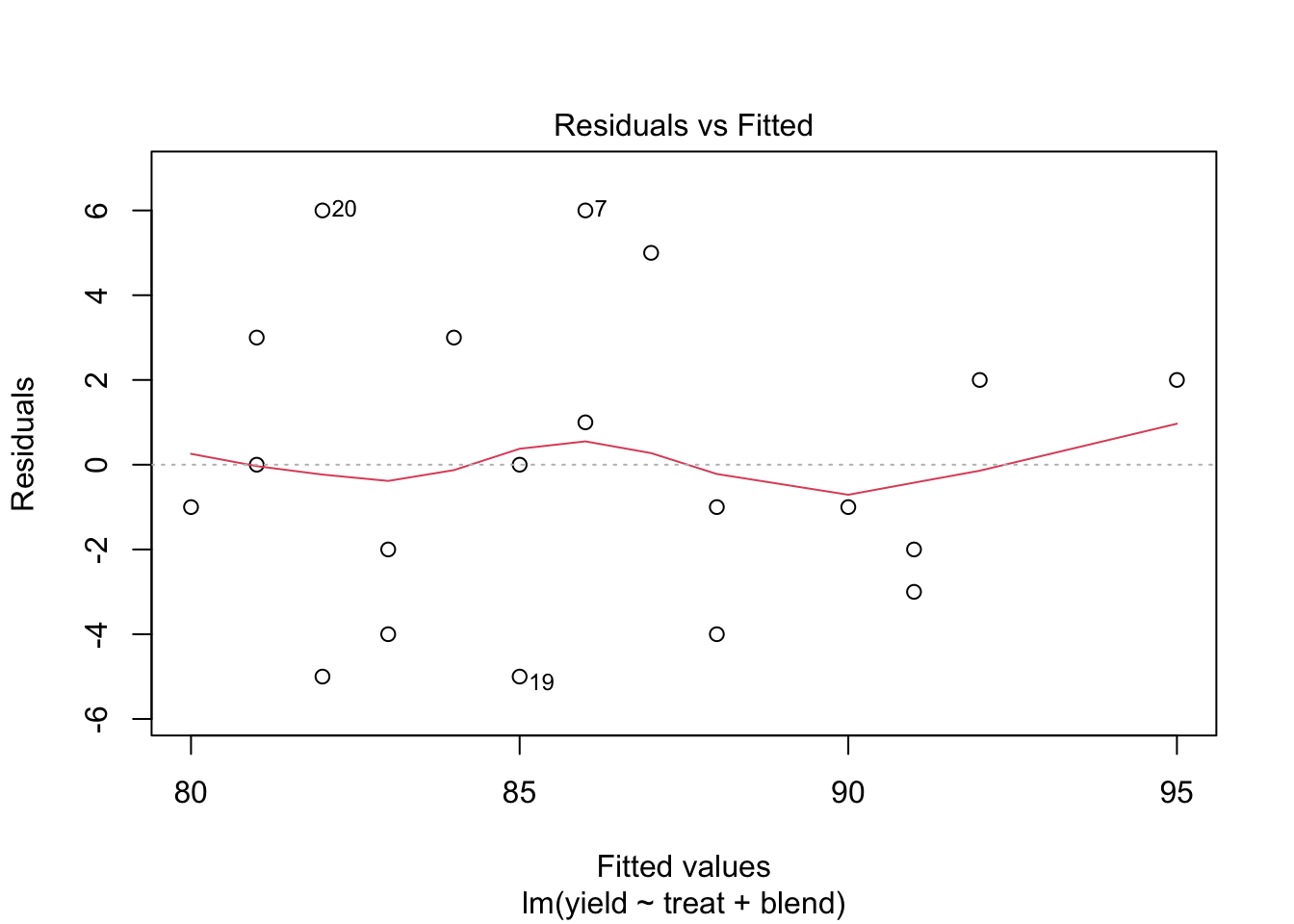
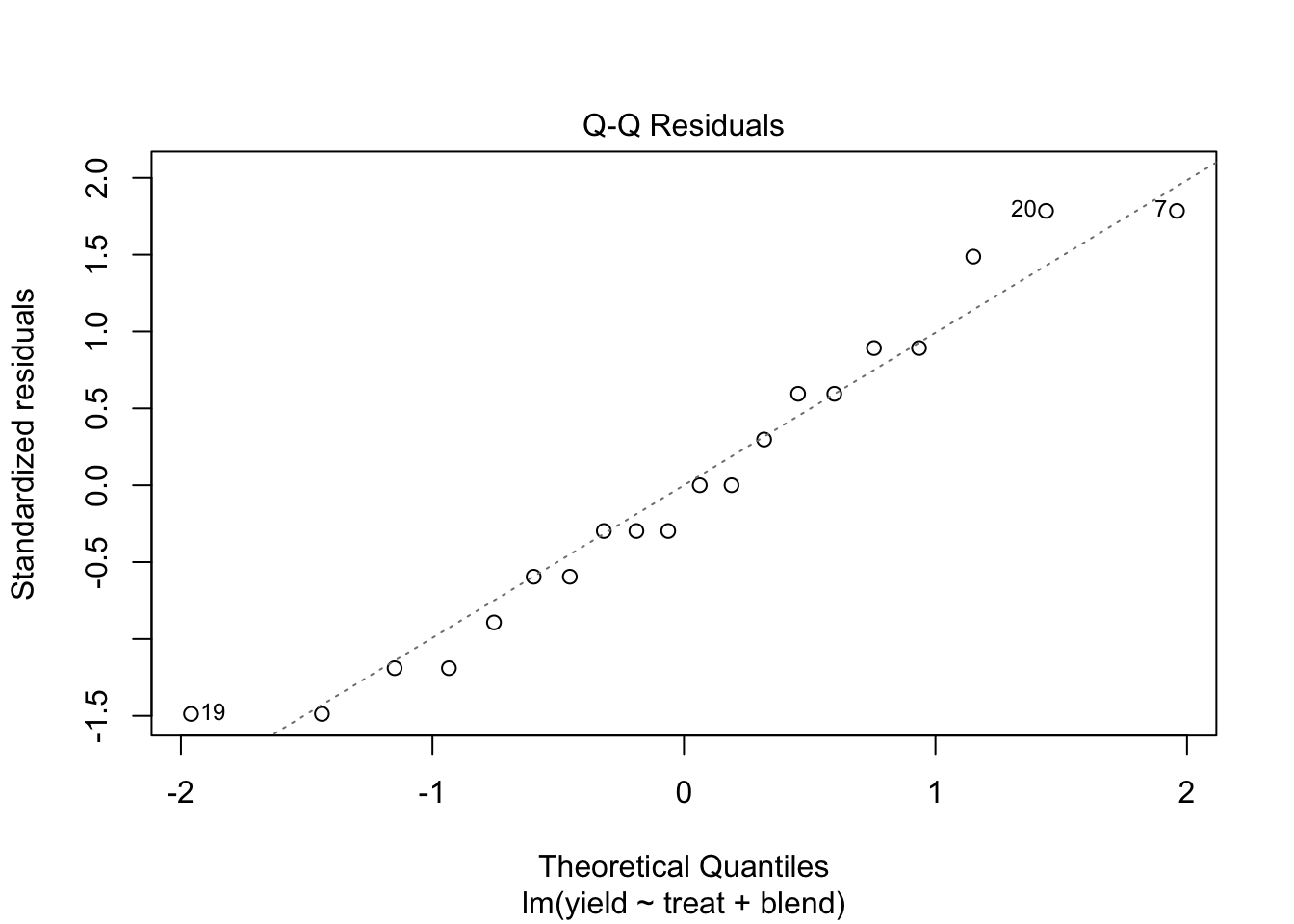
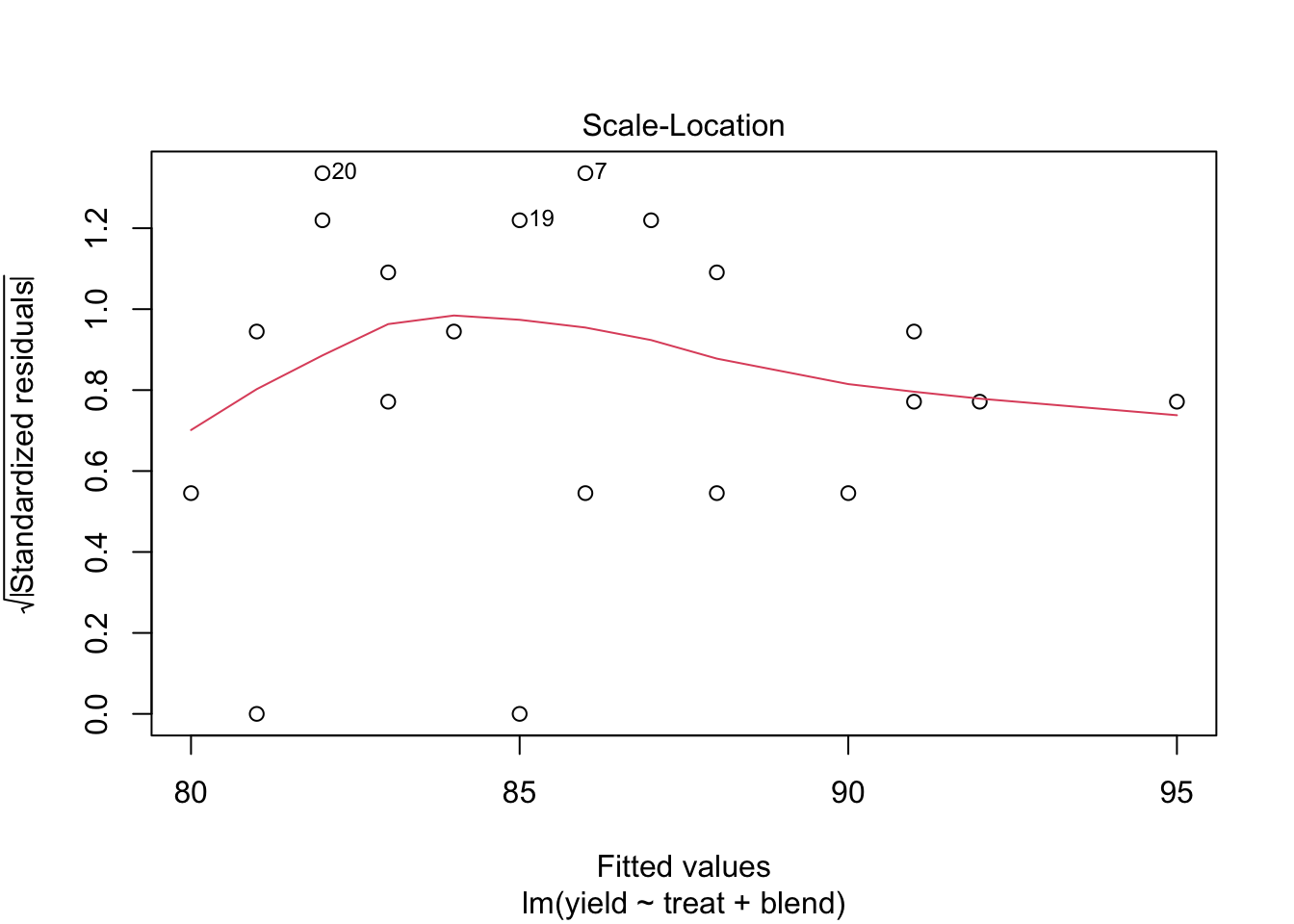
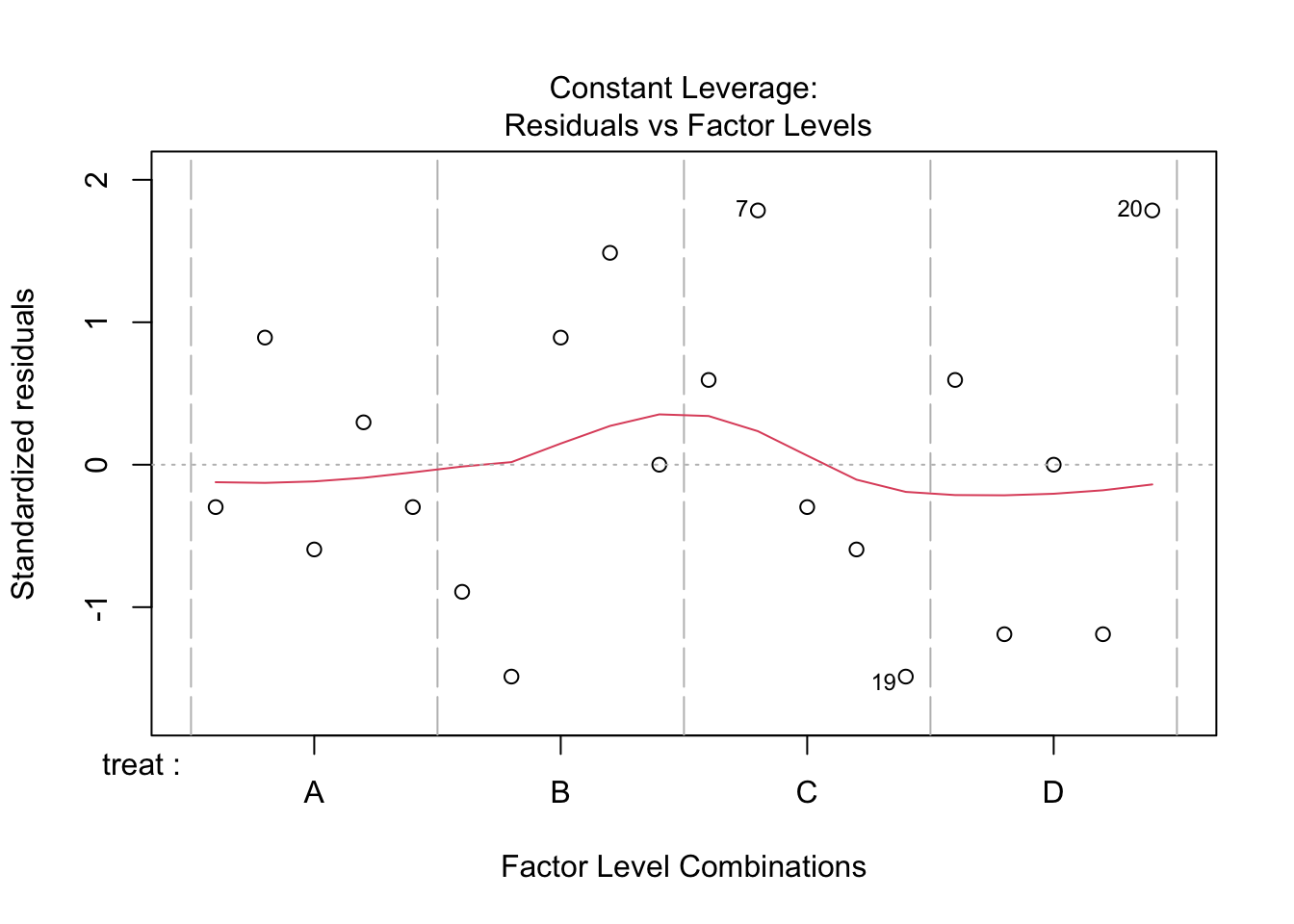
We conclude that the effect of the treatment on the penicillin yield is not significant at the 5% level of significance (p = 0.34.

We also observe that there is a large effect of the blend on the yield. Blend explains about 47.1% of the variability in the penicillin yield.

6 Pseudo-replication

A study on the facultative pathogen Francisella tularensis was conceived by Ramond et al. (2015) [12].

  • F. tularensis enters the cells of its host by phagocytosis.

  • The authors showed that F. tularensis is arginine deficient and imports arginine from the host cell via an arginine transporter, ArgP, in order to efficiently escape from the phagosome and reach the cytosolic compartment, where it can actively multiply.

  • In their study, they compared the proteome of wild type F. tularensis (WT) to ArgP-gene deleted F. tularensis (knock-out, D8).

  • The sample for each bio-rep was run in technical triplicate on the mass-spectrometer.

  • We will use data for the protein 50S ribosomal protein L5 A0Q4J5

6.1 Data exploration

franc <- read_tsv("https://raw.githubusercontent.com/statOmics/PSLSData/main/francisellaA0Q4J5.txt")
## Rows: 18 Columns: 3
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: "\t"
## chr (2): genotype, biorep
## dbl (1): intensityLog2
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.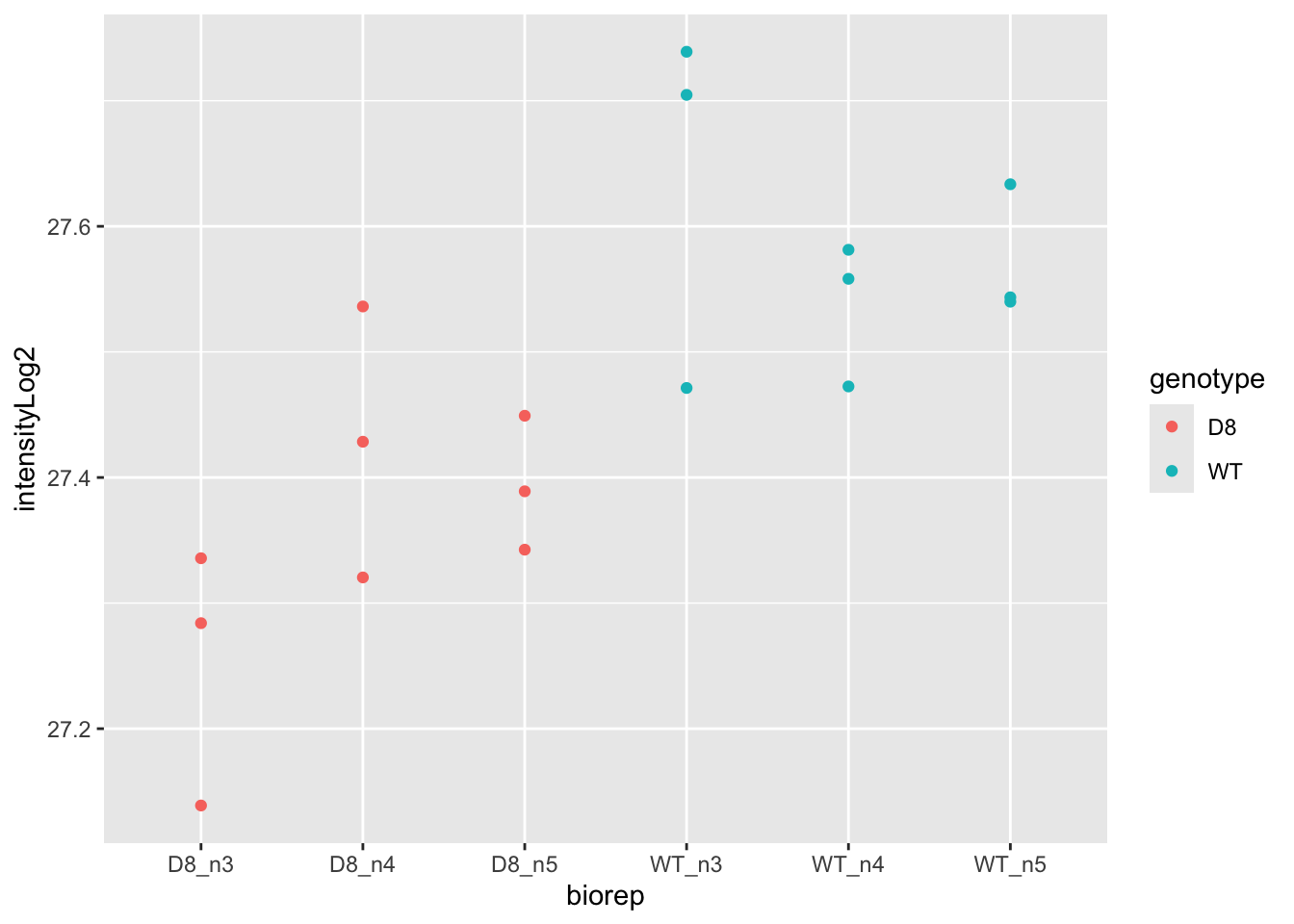
franc
ABCDEFGHIJ0123456789
genotype
<chr>
biorep
<chr>
intensityLog2
<dbl>
WTWT_n327.73900
WTWT_n327.47128
WTWT_n327.70466
WTWT_n427.47251
WTWT_n427.58132
WTWT_n427.55821
WTWT_n527.54348
WTWT_n527.53997
WTWT_n527.63349
D8D8_n327.13884
Next
12
Previous
1-10 of 18 rows
franc %>%
  ggplot(aes(biorep, intensityLog2, color = genotype)) +
  geom_point()

  • Response?
  • Experimental unit?
  • Observational unit?
  • Factors?

→ Pseudo-replication, randomisation to bio-repeat and each bio-repeat measured in technical triplicate. → If we would analyse the data using a linear model based on each measured intensity, we would act as if we had sampled 18 bio-repeats. → Effect of interest has to be assessed between bio-repeats. So block analysis not possible!

If the same number of pseudo-replicates/technical replicates are available for each bio-repeat:

  • average first over bio-repeats to obtain independent measurements
  • averages will then have the same precision
  • assess effect of treatment using averages
  • Caution: never summarize over bio-repeats/experimental units
lmBiorep <- lm(intensityLog2 ~ -1 + biorep, franc)
lmBiorep
## 
## Call:
## lm(formula = intensityLog2 ~ -1 + biorep, data = franc)
## 
## Coefficients:
## biorepD8_n3  biorepD8_n4  biorepD8_n5  biorepWT_n3  biorepWT_n4  biorepWT_n5  
##       27.25        27.43        27.39        27.64        27.54        27.57
francSum <- data.frame(genotype = rep(c("D8", "WT"), each = 3) %>% as.factor() %>% relevel("WT"), intensityLog2 = lmBiorep$coef)
francSum
ABCDEFGHIJ0123456789
 
 
genotype
<fct>
intensityLog2
<dbl>
biorepD8_n3D827.25286
biorepD8_n4D827.42836
biorepD8_n5D827.39357
biorepWT_n3WT27.63831
biorepWT_n4WT27.53734
biorepWT_n5WT27.57232
6 rows
lmSum <- lm(intensityLog2 ~ genotype, francSum)
summary(lmSum)
## 
## Call:
## lm(formula = intensityLog2 ~ genotype, data = francSum)
## 
## Residuals:
## biorepD8_n3 biorepD8_n4 biorepD8_n5 biorepWT_n3 biorepWT_n4 biorepWT_n5 
##    -0.10541     0.07010     0.03531     0.05566    -0.04531    -0.01034 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 27.58266    0.04333 636.581 3.65e-11 ***
## genotypeD8  -0.22439    0.06128  -3.662   0.0215 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.07505 on 4 degrees of freedom
## Multiple R-squared:  0.7702, Adjusted R-squared:  0.7128 
## F-statistic: 13.41 on 1 and 4 DF,  p-value: 0.02154

6.2 Wrong analysis

lmWrong <- lm(intensityLog2 ~ genotype, franc)
summary(lmWrong)
## 
## Call:
## lm(formula = intensityLog2 ~ genotype, data = franc)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.21943 -0.04181 -0.01914  0.06537  0.17792 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 27.35826    0.03457  791.48  < 2e-16 ***
## genotypeWT   0.22439    0.04888    4.59 0.000302 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1037 on 16 degrees of freedom
## Multiple R-squared:  0.5684, Adjusted R-squared:  0.5414 
## F-statistic: 21.07 on 1 and 16 DF,  p-value: 0.0003017

Note, that the analysis where we ignore that we have multiple technical repeats for each bio-repeat returns results that are much more significant because we act as if we have much more independent observations.

6.2.1 No Type I error control!

sigmaWithin <- sigma(lmBiorep)
sigmaBetween <- sigma(lmSum)
xBiorep <- model.matrix(~ -1 + biorep, franc)
xWrong <- model.matrix(~genotype, franc)


set.seed(2523)
nSim <- 1000
resWrong <- matrix(NA, nSim, 4) %>% as.data.frame()
names(resWrong) <- c("Estimate", "Std. Error", "t value", "pvalue")
resCorrect <- resWrong
genotype <- franc$genotype
genotypeSum <- francSum$genotype
biorep <- franc$biorep

for (i in 1:nSim)
{
  biorepSim <- rnorm(ncol(xBiorep), sd = sigmaBetween)
  ySim <- xBiorep %*% biorepSim + rnorm(nrow(xBiorep), sd = sigmaWithin)
  ySum <- lm(ySim ~ biorep)$coefficient
  resWrong[i, ] <- summary(lm(ySim ~ genotype))$coefficient[2, ]
  resCorrect[i, ] <- summary(lm(ySum ~ genotypeSum))$coefficient[2, ]
}
mean(resCorrect$pvalue < 0.05)
## [1] 0.042
mean(resWrong$pvalue < 0.05)
## [1] 0.143
qplot(resCorrect$pvalue, geom = "histogram", boundary = c(0, 1)) +
  stat_bin(breaks = seq(0, 1, .1)) +
  xlab("pvalue") +
  ggtitle("Correct analysis")
## Warning: `qplot()` was deprecated in ggplot2 3.4.0.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Computation failed in `stat_bin()`.
## Caused by error in `seq.default()`:
## ! 'from' must be of length 1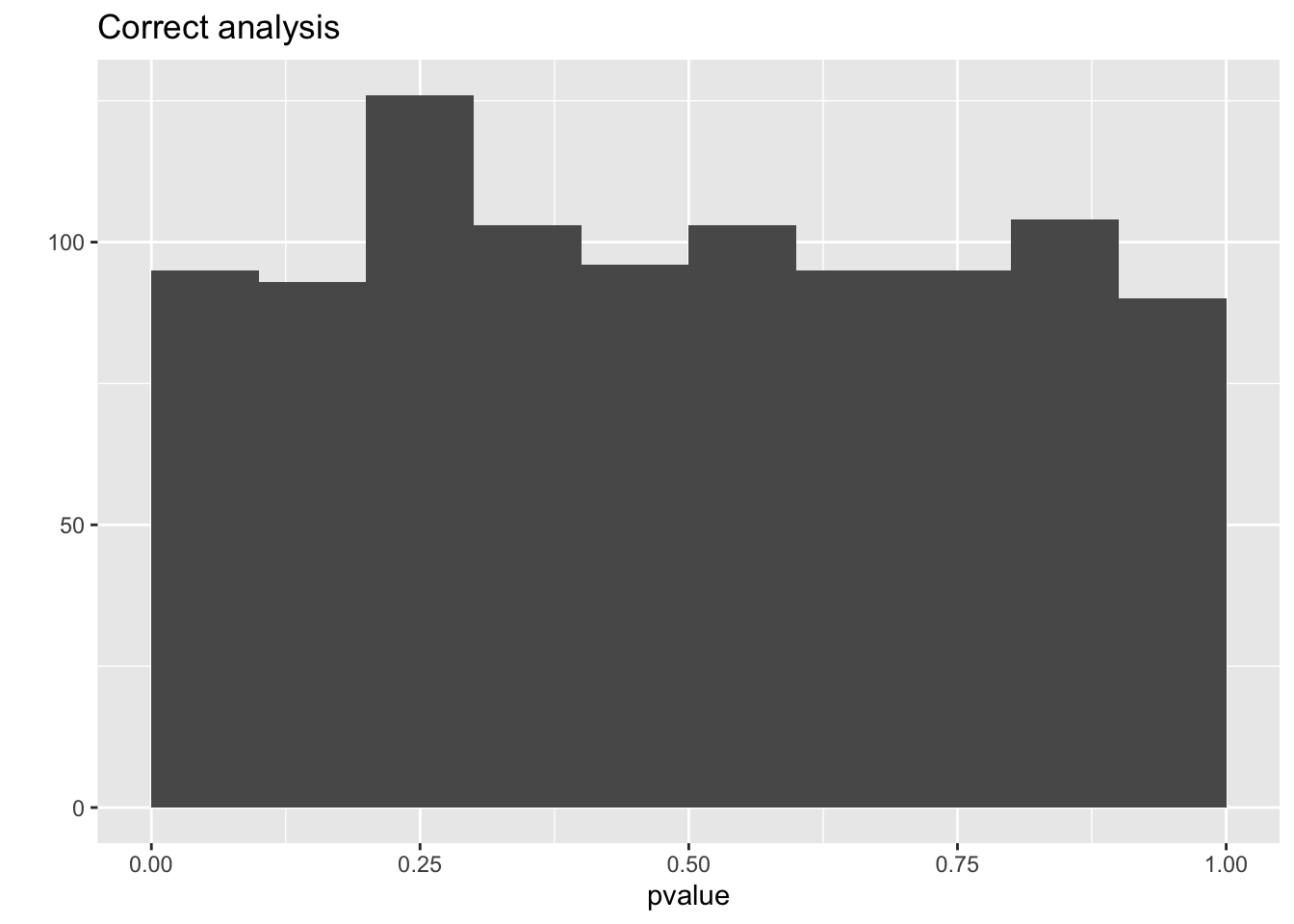

qplot(resWrong$pvalue, geom = "histogram", boundary = c(0, 1)) +
  stat_bin(breaks = seq(0, 1, .1)) +
  xlab("pvalue") +
  ggtitle("Wrong analysis")
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Computation failed in `stat_bin()`.
## Caused by error in `seq.default()`:
## ! 'from' must be of length 1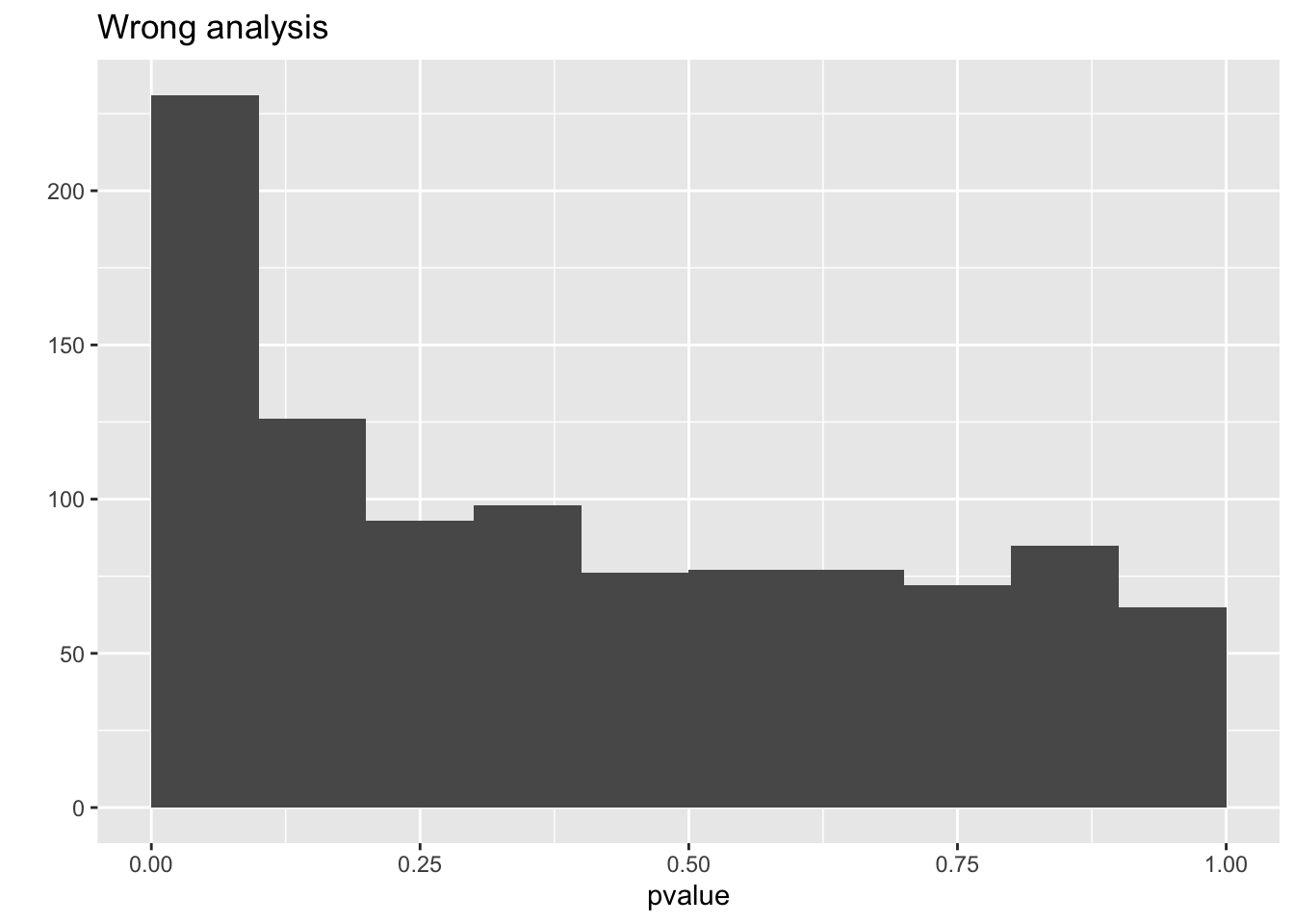

  • So we observe that the analysis that does not account for pseudo-replication is too liberal!

  • The analysis that first summarizes over the technical repeats leads to correct p-values and correct type I error control!

  • What to do when you have an unequal number of technical repeats: more advanced methods are required

    • e.g. mixed models
    • The mixed model framework can model the correlation structure in the data

  • Mixed models can also be used when inference between and within blocks is needed, e.g. split-plot designs.

  • But, mixed models are beyond the scope of the lecture series.

LS0tCnRpdGxlOiAiOC4zIEV4cGVyaW1lbnRhbCBEZXNpZ24gSUk6IFJhbmRvbWl6ZWQgQ29tcGxldGUgQmxvY2sgRGVzaWducyBhbmQgUHNldWRvLXJlcGxpY2F0aW9uIgphdXRob3I6ICJMaWV2ZW4gQ2xlbWVudCIKZGF0ZTogInN0YXRPbWljcywgR2hlbnQgVW5pdmVyc2l0eSAoaHR0cHM6Ly9zdGF0b21pY3MuZ2l0aHViLmlvKSIKb3V0cHV0OgogIGJvb2tkb3duOjpwZGZfZG9jdW1lbnQyOgogICAgdG9jOiB0cnVlCiAgICBudW1iZXJfc2VjdGlvbnM6IHRydWUKICAgIGxhdGV4X2VuZ2luZTogeGVsYXRleAphbHdheXNfYWxsb3dfaHRtbDogdHJ1ZQotLS0KCgo8YSByZWw9ImxpY2Vuc2UiIGhyZWY9Imh0dHBzOi8vY3JlYXRpdmVjb21tb25zLm9yZy9saWNlbnNlcy9ieS1uYy1zYS80LjAiPjxpbWcgYWx0PSJDcmVhdGl2ZSBDb21tb25zIExpY2Vuc2UiIHN0eWxlPSJib3JkZXItd2lkdGg6MCIgc3JjPSJodHRwczovL2kuY3JlYXRpdmVjb21tb25zLm9yZy9sL2J5LW5jLXNhLzQuMC84OHgzMS5wbmciIC8+PC9hPgoKYGBge3J9CmxpYnJhcnkodGlkeXZlcnNlKQpgYGAKCiMgUmFuZG9taXplZCBjb21wbGV0ZSBibG9jayBkZXNpZ25zCgpcW1xzaWdtYV4yPSBcc2lnbWFeMl97YmlvfStcc2lnbWFeMl9cdGV4dHtsYWJ9ICtcc2lnbWFeMl9cdGV4dHtleHRyYWN0aW9ufSArIFxzaWdtYV4yX1x0ZXh0e3J1bn0gKyBcbGRvdHNcXQoKLSBCaW9sb2dpY2FsOiBmbHVjdHVhdGlvbnMgaW4gcHJvdGVpbiBsZXZlbCBiZXR3ZWVuIG1pY2UsIGZsdWN0YXRpb25zIGluIHByb3RlaW4gbGV2ZWwgYmV0d2VlbiBjZWxscywgLi4uCi0gVGVjaG5pY2FsOiBjYWdlIGVmZmVjdCwgbGFiIGVmZmVjdCwgd2VlayBlZmZlY3QsIHBsYXNtYSBleHRyYWN0aW9uLCBNUy1ydW4sIC4uLgoKIyBOYXR1cmUgbWV0aG9kczogUG9pbnRzIG9mIHNpZ25pZmljYW5jZSAtIEJsb2NraW5nCltodHRwczovL3d3dy5uYXR1cmUuY29tL2FydGljbGVzL25tZXRoLjMwMDUucGRmXShodHRwczovL3d3dy5uYXR1cmUuY29tL2FydGljbGVzL25tZXRoLjMwMDUucGRmKQoKLSBPbmV3YXkgYW5vdmEgaXMgYSBzcGVjaWFsIGNhc2Ugb2YgYSBjb21wbGV0ZWx5IHJhbmRvbWl6ZWQgZGVzaWduOgoKICAgIC0gdGhlIGV4cGVyaW1lbnRhbCB1bml0cyBhcmUgc2FtcGxlZCBhdCByYW5kb20gZnJvbSB0aGUgcG9wdWxhdGlvbgogICAgLSB0aGUgdHJlYXRtZW50cyBhcmUgcmFuZG9taXplZCB0byB0aGUgZXhwZXJpbWVudGFsIHVuaXRzCiAgICAtIEV2ZXJ5IGV4cGVyaW1lbnRhbCB1bml0IHJlY2VpdmVzIG9uZSB0cmVhdG1lbnQgYW5kIGl0cyByZXNwb25zZSB2YXJpYWJsZSBpcyBtZWFzdXJlZCBvbmNlLgoKLSBJbiBhIGJsb2NrIGRlc2lnbiB0aGUgZXhwZXJpbWVudGFsIHVuaXRzIGFyZSBibG9ja3Mgd2hpY2ggYXJlIHNhbXBsZWQgYXQgcmFuZG9tIG9mIHRoZSBwb3B1bGF0aW9uIG9mIGFsbCBwb3NzaWJsZSBibG9ja3MuCgogICAgLSBUaGUgUkNCIHJlc3RyaWN0cyByYW5kb21pemF0aW9uOiB0aGUgdHJlYXRtZW50cyBhcmUgcmFuZG9taXplZCB3aXRoaW4gdGhlIGJsb2Nrcy4KICAgIC0gaXQgY2Fubm90IGJlIGFuYWx5c2VkIHVzaW5nIG9uZXdheSBhbm92YS4KICAgIC0gVGhlIHBhaXJlZCBkZXNpZ24gaXMgYSBzcGVjaWFsIGNhc2Ugb2YgYW4gUkNCOiBibG9jayBzaXplIGVxdWFscyAyLgogICAgLSBXaXRoaW4gYmxvY2sgZWZmZWN0cyBjYW4gYmUgYXNzZXNzZWQgdXNpbmcgdGhlIGxtIGZ1bmN0aW9uIGluIFIuCgojIE1vdXNlIGV4YW1wbGUKCiMjIEJhY2tncm91bmQKCmBgYHtyIGVjaG89RkFMU0UsIG91dC53aWR0aD0iNTAlIn0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoIi4vZmlndXJlcy9tb3VzZVRjZWxsX1JDQl9kZXNpZ24ucG5nIikKYGBgCgpEdWd1ZXQgZXQgYWwuICgyMDE3KSBNQ1AgMTYoOCk6MTQxNi0xNDMyLiBkb2k6IDEwLjEwNzQvbWNwLm0xMTYuMDYyNzQ1CgotIEFsbCB0cmVhdG1lbnRzIG9mIGludGVyZXN0IGFyZSBwcmVzZW50IHdpdGhpbiBibG9jayEKLSBXZSBjYW4gZXN0aW1hdGUgdGhlIGVmZmVjdCBvZiB0aGUgdHJlYXRtZW50IHdpdGhpbiBibG9jayEKCldlIGZvY3VzIG9uIG9uZSBwcm90ZWluCgogIC0gVGhlIG1lYXN1cmVkIGludGVuc2l0aWVzIGFyZSBhbHJlYWR5IG9uIHRoZSBsb2cyLXNjYWxlLiBEaWZmZXJlbmNlcyBiZXR3ZWVuIHRoZSBpbnRlbnNpdGllcyBjYW4gdGh1cyBiZSBpbnRlcnByZXRlZCBhcyBsb2cyIEZDLgogIC0gUDE2MDQ1IG9yIEdhbGVjdGluLTEuCiAgLSBGdW5jdGlvbjogIkxlY3RpbiB0aGF0IGJpbmRzIGJldGEtZ2FsYWN0b3NpZGUgYW5kIGEgd2lkZSBhcnJheSBvZiBjb21wbGV4IGNhcmJvaHlkcmF0ZXMuIFBsYXlzIGEgcm9sZSBpbiByZWd1bGF0aW5nIGFwb3B0b3NpcywgY2VsbCBwcm9saWZlcmF0aW9uIGFuZCBjZWxsIGRpZmZlcmVudGlhdGlvbi4gSW5oaWJpdHMgQ0Q0NSBwcm90ZWluIHBob3NwaGF0YXNlIGFjdGl2aXR5IGFuZCB0aGVyZWZvcmUgdGhlIGRlcGhvc3Bob3J5bGF0aW9uIG9mIEx5biBraW5hc2UuIFN0cm9uZyBpbmR1Y2VyIG9mIFQtY2VsbCBhcG9wdG9zaXMuIiAoc291cmNlOiBbdW5pcHJvdF0oaHR0cHM6Ly93d3cudW5pcHJvdC5vcmcvdW5pcHJvdC9QMTYwNDUpKQoKIyMgRGF0YSBFeHBsb3JhdGlvbgoKYGBge3J9Cm1vdXNlIDwtIHJlYWRfdHN2KCJodHRwczovL3Jhdy5naXRodWJ1c2VyY29udGVudC5jb20vc3RhdE9taWNzL1BTTFNEYXRhL21haW4vbW91c2VQMTYwNDUudHh0IikKbW91c2UKYGBgCgoKYGBge3J9Cm1vdXNlICU+JQogIGdncGxvdChhZXMoeCA9IG1vdXNlLCB5ID0gaW50ZW5zaXR5LCBjb2wgPSBjZWxsdHlwZSkpICsKICBnZW9tX3BvaW50KCkKYGBgCgpgYGB7cn0KbW91c2UgJT4lCiAgZ2dwbG90KGFlcyh4ID0gY2VsbHR5cGUsIHkgPSBpbnRlbnNpdHkpKSArCiAgZ2VvbV9wb2ludCgpICsKICBnZW9tX2xpbmUoYWVzKGdyb3VwID0gbW91c2UpKSArCiAgZ2VvbV9wb2ludChhZXMoY29sID0gY2VsbHR5cGUpKQpgYGAKCgpUaGUgcGxvdHMgc2hvdyBldmlkZW5jZSBmb3IKLSBhbiB1cHJlZ3VsYXRpb24gb2YgdGhlIHByb3RlaW4gZXhwcmVzc2lvbiBpbiByZWd1bGF0b3J5IFQtY2VsbHMgYW5kCi0gYSBjb25zaWRlcmFibGUgdmFyaWFiaWxpdHkgaW4gZXhwcmVzc2lvbiBmcm9tIGFuaW1hbCB0byBhbmltYWwhCgojIyBQYWlyZWQgQW5hbHlzaXMKClRoaXMgaXMgYSBwYWlyZWQgZGVzaWduLCB3aGljaCBpcyB0aGUgbW9zdCBzaW1wbGUgZm9ybSBvZiByYW5kb21pemVkIGNvbXBsZXRlIGJsb2NrIGRlc2lnbi4KCkluIHRoZSBpbnRyb2R1Y3Rpb24gdG8gc3RhdGlzdGljYWwgaW5mZXJlbmNlIHdlIHdvdWxkIGhhdmUgYW5hbHl6ZWQgdGhlIGRhdGEgYnkgZGlmZmVyZW5jaW5nLgoKYGBge3J9Cm1vdXNlV2lkZSA8LSBtb3VzZSAlPiUKICBzcHJlYWQoY2VsbHR5cGUsIGludGVuc2l0eSkgJT4lCiAgbXV0YXRlKGRlbHRhID0gVHJlZyAtIFRjb24pCm1vdXNlV2lkZQpgYGAKCiMjIyBEYXRhIGV4cGxvcmF0aW9uCgotIEJveHBsb3Qgb2YgZGlmZmVyZW5jZQoKYGBge3J9Cm1vdXNlV2lkZSAlPiUKICBnZ3Bsb3QoYWVzKHggPSAiIiwgeSA9IGRlbHRhKSkgKwogIGdlb21fYm94cGxvdChvdXRsaWVyLnNoYXBlID0gTkEpICsKICBnZW9tX2ppdHRlcigpCmBgYAoKLSBTdW1tYXJ5IHN0YXRpc3RpY3MKYGBge3J9CmRlbHRhU3VtIDwtIG1vdXNlV2lkZSAlPiUKICBzdW1tYXJpemUoCiAgICAgIG1lYW4gPSBtZWFuKGRlbHRhLCBuYS5ybSA9IFRSVUUpLAogICAgICBzZCA9IHNkKGRlbHRhLCBuYS5ybSA9IFRSVUUpLAogICAgICBuID0gbigpCiAgKSAlPiUKICBtdXRhdGUoc2UgPSBzZCAvIHNxcnQobikpCmRlbHRhU3VtCmBgYAoKCk5vdGUsIHRoYXQgdGhlIGludGVuc2l0eSBkYXRhIGFyZSBub3QgaW5kZXBlbmRlbnQgYmVjYXVzZSB3ZSBtZWFzdXJlZCB0aGUgZXhwcmVzc2lvbiBpbiByZWd1bGF0b3J5IGFuZCBvcmRpbmFyeSBULWNlbGxzIGZvciBldmVyeSBhbmltYWwKCi0gQ292YXJpYW5jZSBhbmQgY29ycmVsYXRpb24gYmV0d2VlbiBleHByZXNzaW9uIGluIGJvdGggY2VsbHR5cGVzCgpgYGB7cn0KY29yKG1vdXNlV2lkZVssIGMoIlRjb24iLCAiVHJlZyIpXSkKdmFyKG1vdXNlV2lkZVssIGMoIlRjb24iLCAiVHJlZyIpXSkKdmFyKG1vdXNlV2lkZVssIGMoIlRjb24iLCAiVHJlZyIpXSkgJT4lCiAgZGlhZygpICU+JQogIHNxcnQoKQpgYGAKCi0gVGhlcmUgaXMgaW5kZWVkIGEgbGFyZ2UgY29ycmVsYXRpb24gYmV0d2VlbiB0aGUgZXhwcmVzc2lvbiBvZiB0aGUgcHJvdGVpbiBpbiBjb252ZW50aW9uYWwgYW5kIHJlZ3VsYXRvcnkgVC1jZWxscy4KCi0gU3RhbmRhcmQgZGV2aWF0aW9uIG9mIGRpZmZlcmVuY2U/CgokJApcYmVnaW57YXJyYXl9e2xjbH0KXHRleHR7c2R9X3t4X3IgLSB4X2N9ICY9JiBcc3FydHsxXjJcaGF0IFxzaWdtYV9yXjIgKyAoLTEpXjIgXGhhdCBcc2lnbWFfY14yICsgMiBcdGltZXMgMQpcdGltZXMgLTEKXHRpbWVzIFxoYXRcc2lnbWFfe3IsY319XFwKJj0mXHNxcnR7XGhhdCBcc2lnbWFfcl4yICsgXGhhdCBcc2lnbWFfY14yIC0gMiBcdGltZXMgXGhhdFxzaWdtYV97cixjfX0KXGVuZHthcnJheX0KJCQKCmBgYHtyfQpzZERlbHRhMiA8LSAoYygtMSwgMSkgJSolIHZhcihtb3VzZVdpZGVbLCBjKCJUY29uIiwgIlRyZWciKV0pICUqJSBjKC0xLCAxKSkgJT4lCiAgc3FydCgpCnNkRGVsdGEyCgpzZURlbHRhQmFyIDwtIHNkRGVsdGEyIC8gc3FydChkZWx0YVN1bSRuKQpzZURlbHRhQmFyCgpkZWx0YVN1bQpgYGAKCi0gVGhlIHN0YW5kYXJkIGRldmlhdGlvbiBvbiB0aGUgZGlmZmVyZW5jZSBpcyBtdWNoIGxvd2VyIGJlY2F1c2Ugb2YgdGhlIHN0cm9uZyBjb3JyZWxhdGlvbiEKLSBOb3RlLCB0aGF0IHRoZSBwYWlyZWQgZGVzaWduIGVuYWJsZWQgdXMgdG8gZXN0aW1hdGUgdGhlIGRpZmZlcmVuY2UgaW4gbG9nMi1leHByZXNzaW9uIGJldHdlZW4gdGhlIHR3byBjZWxsIHR5cGVzIGluIGV2ZXJ5IGFuaW1hbCAobG9nMiBGQykuCgoKYGBge3J9CnQudGVzdChkZWx0YX4xLCBtb3VzZVdpZGUpCmBgYAoKIyMgUmFuZG9taXplZCBjb21wbGV0ZSBibG9jayBhbmFseXNpcwoKV2UgY2FuIGFsc28gYW5hbHlzZSB0aGUgZGVzaWduIHVzaW5nIGEgbGluZWFyIG1vZGVsLCBpLmUuIHdpdGgKCi0gYSBtYWluIGVmZmVjdCBmb3IgY2VsbCB0eXBlIGFuZAotIGEgbWFpbiBlZmZlY3QgZm9yIHRoZSBibG9jayBmYWN0b3IgbW91c2UKCkJlY2F1c2Ugd2UgaGF2ZSBtZWFzdXJlZCB0aGUgdHdvIGNlbGwgdHlwZXMgaW4gZXZlcnkgbW91c2UsIHdlIGNhbiB0aHVzIGVzdGltYXRlIHRoZSBhdmVyYWdlIGxvZzItaW50ZW5zaXR5IG9mIHRoZSBwcm90ZWluIGluIHRoZSBULWNlbGxzIGZvciBlYWNoIG1vdXNlLgoKYGBge3J9CmxtUkNCIDwtIGxtKGludGVuc2l0eSB+IGNlbGx0eXBlICsgbW91c2UsIG1vdXNlKQpwbG90KGxtUkNCLCB3aGljaCA9IGMoMSwgMiwgMykpCmBgYAoKSWYgeW91IGhhdmUgZG91YnRzIG9uIHRoYXQgeW91ciBkYXRhIHZpb2xhdGVzIHRoZSBhc3N1bXB0aW9ucyB5b3UgY2FuIGFsd2F5cyBzaW11bGF0ZSBkYXRhIGZyb20gYSBtb2RlbCB3aXRoIHNpbWlsYXIgZWZmZWN0cyBhcyB5b3VycyBidXQgd2hlcmUgYXJlIGRpc3RyaWJ1dGlvbmFsIGFzc3VtcHRpb25zIGhvbGQgYW5kIGNvbXBhcmUgdGhlIHJlc2lkdWFsIHBsb3RzLgoKYGBge3J9CmRlc2lnbiA8LSBtb2RlbC5tYXRyaXgoaW50ZW5zaXR5IH4gY2VsbHR5cGUgKyBtb3VzZSwgbW91c2UpCnNpZ21hTW91c2UgPC0gc3FydChjYXI6OkFub3ZhKGxtUkNCLCB0eXBlID0gIklJSSIpWyJtb3VzZSIsICJTdW0gU3EiXSAvIGNhcjo6QW5vdmEobG1SQ0IsIHR5cGUgPSAiSUlJIilbIm1vdXNlIiwgIkRmIl0pCmJldGFzIDwtIGxtUkNCJGNvZWZmaWNpZW50cwpuTW91c2UgPC0gbW91c2UkbW91c2UgJT4lCiAgdW5pcXVlKCkgJT4lCiAgbGVuZ3RoKCkKCnBhcihtZnJvdyA9IGMoMywgMykpCmZvciAoaSBpbiAxOjkpCnsKICBtb3VzZUVmZmVjdCA8LSBybm9ybShuTW91c2UsIHNkID0gc2lnbWFNb3VzZSkKICBiZXRhc01vdXNlIDwtIG1vdXNlRWZmZWN0Wy0xXSAtIG1vdXNlRWZmZWN0WzFdCiAgYmV0YXNbLWMoMToyKV0gPC0gYmV0YXNNb3VzZQogIHlzaW0gPC0gZGVzaWduICUqJSBiZXRhcyArIHJub3JtKG5yb3coZGVzaWduKSwgc2QgPSBzaWdtYShsbVJDQikpCiAgcGxvdChsbSh5c2ltIH4gLTEgKyBkZXNpZ24pLCB3aGljaCA9IDEpCn0KYGBgCgpUaGUgZGV2aWF0aW9ucyBzZWVuIGluIG91ciBwbG90IGFyZSBpbiBsaW5lIHdpdGggd2hhdCB0aG9zZSBvYnNlcnZlZCBpbiBzaW11bGF0aW9ucyB1bmRlciB0aGUgbW9kZWwgYXNzdW1wdGlvbnMuCkhlbmNlLCB3ZSBjYW4gdXNlIHRoZSBtb2RlbCBmb3Igc3RhdGlzdGljYWwgaW5mZXJlbmNlLgoKYGBge3J9CmFub3ZhUkNCIDwtIGNhcjo6QW5vdmEobG1SQ0IsIHR5cGUgPSAiSUlJIikKc3VtbWFyeShsbVJDQikKdC50ZXN0KGRlbHRhIH4xICwgbW91c2VXaWRlKQphbm92YVJDQgpgYGAKCk5vdGljZSB0aGF0CgoxLiB0aGUgZXN0aW1hdGUsIHNlLCB0LXRlc3Qgc3RhdGlzdGljIGFuZCBwLXZhbHVlIGZvciB0aGUgY2VsbHR5cGUgZWZmZWN0IG9mIGludGVyZXN0IGlzIHRoZSBzYW1lIGFzIGluIHRoZSBwYWlyZWQgdC10ZXN0IQoKMi4gdGhlIGFub3ZhIGFuYWx5c2lzIHNob3dzIHRoYXQgd2UgbW9kZWwgdGhlIHRvdGFsIHZhcmlhYmlsaXR5IGluIHRoZSBwcm90ZWluIGV4cHJlc3Npb24gaW4gVC1jZWxscyB1c2luZyAgdmFyaWFiaWxpdHkgZHVlIHRvIHRoZSBjZWxsIHR5cGUgKENUKSwgdGhlIHZhcmlhYmlsaXR5IGZyb20gbW91c2UgdG8gbW91c2UgKE0pIGFuZCByZXNpZHVhbCB2YXJpYWJpbGl0eSAoUikgd2l0aGluIG1vdXNlIHRoYXQgd2UgY2Fubm90IGV4cGxhaW4uIEluZGVlZCwKCiQkClxiZWdpbnthcnJheX17bGNsfQpcdGV4dHtTU1RvdH0gJj0mIFx0ZXh0e1NTQ1R9ICsgXHRleHR7U1NNfSArIFx0ZXh0e1NTRX1cXApgciByb3VuZChhbm92YVJDQlstMSwiU3VtIFNxIl0gJT4lIHN1bSgpLDEpYCAmPSYgYHIgcm91bmQoYW5vdmFSQ0JbImNlbGx0eXBlIiwiU3VtIFNxIl0sMSlgICsgYHIgcm91bmQoYW5vdmFSQ0JbIm1vdXNlIiwiU3VtIFNxIl0sMSlgICsgYHIgcm91bmQoYW5vdmFSQ0JbIlJlc2lkdWFscyIsIlN1bSBTcSJdLDEpYApcZW5ke2FycmF5fQokJAoKU28gdGhlIGNlbGx0eXBlIGFuZCB0aGUgbW91c2UgZWZmZWN0IGV4cGxhaW4gcmVzcGVjdGl2ZWx5CiQkClxiZWdpbnthcnJheX17bGx9ClxmcmFje1x0ZXh0e1NTQ1R9fXtcdGV4dHtTU1RvdH19XHRpbWVzIDEwMCZcZnJhY3tcdGV4dHtTU019fXtcdGV4dHtTU1RvdH19XHRpbWVzIDEwMFxcXFwKYHIgcm91bmQoYW5vdmFSQ0JbImNlbGx0eXBlIiwiU3VtIFNxIl0vc3VtKGFub3ZhUkNCWy0xLCJTdW0gU3EiXSkqMTAwLDEpYCYKYHIgcm91bmQoYW5vdmFSQ0JbIm1vdXNlIiwiU3VtIFNxIl0vc3VtKGFub3ZhUkNCWy0xLCJTdW0gU3EiXSkqMTAwLDEpYFxcClxlbmR7YXJyYXl9CiQkCgpwZXJjZW50IG9mIHRoZSB2YXJpYWJpbGl0eSBpbiB0aGUgcHJvdGVpbiBleHByZXNzaW9uIHZhbHVlcyBhbmQKJCQKXGZyYWN7XHRleHR7U1NFfX17XHRleHR7U1NUb3R9fSBcdGltZXMgMTAwID0gYHIgcm91bmQoYW5vdmFSQ0JbIlJlc2lkdWFscyIsIlN1bSBTcSJdL3N1bShhbm92YVJDQlstMSwiU3VtIFNxIl0pKjEwMCwxKWAKJCQKcGVyY2VudCBjYW5ub3QgYmUgZXhwbGFpbmVkLgoKTm90ZSwgdGhhdAoKLSB0aGUgdmFyaWFiaWxpdHkgZnJvbSBtb3VzZSB0byBtb3VzZSBpcyB0aGUgbGFyZ2VzdCBzb3VyY2Ugb2YgdmFyaWFiaWxpdHkgaW4gdGhlIG1vZGVsLAotIFRoaXMgdmFyaWFiaWxpdHkgY2FuIGJlIGVzdGltYXRlZCB3aXRoIHRoZSBSQ0IgZGVzaWduIGFuZAotIGNhbiB0aHVzIGJlIGlzb2xhdGVkIGZyb20gdGhlIHJlc2lkdWFsIHZhcmlhYmlsaXR5Ci0gbGVhZGluZyB0byBhIG11Y2ggaGlnaGVyIHByZWNpc2lvbiBvbiB0aGUgZXN0aW1hdGUgb2YgdGhlIGF2ZXJhZ2UgbG9nMiBGQyBiZXR3ZWVuIHJlZ3VsYXRvcnkgYW5kIGNvbnZlbnRpb25hbCBULWNlbGxzIHRoYXQgd2hhdCB3b3VsZCBiZSBvYnRhaW5lZCB3aXRoIGEgQ1JEIQoKTm90ZSwgdGhhdCB0aGUgUkNCIGFsc28gaGFzIHRvIHNhY3JpZmljZSBhIG51bWJlciBvZiBkZWdyZWVzIG9mIGZyZWVkb20gdG8gZXN0aW1hdGUgdGhlIG1vdXNlIGVmZmVjdCwgaGVyZSA2IERGLgoKSGVuY2UsIHRoZSBwb3dlciBnYWluIG9mIHRoZSBSQ0IgaXMgYSB0cmFkZS1vZmYgYmV0d2VlbiB0aGUgdmFyaWFiaWxpdHkgdGhhdCBjYW4gYmUgZXhwbGFpbmVkIGJ5IHRoZSBibG9jayBlZmZlY3QgYW5kIHRoZSBsb3NzIGluIERGLgoKPCEtLQpJZiB5b3UgcmVtZW1iZXIgdGhlIGVxdWF0aW9uIG9mIHZhcmlhbmNlIGNvdmFyaWFuY2UgbWF0cml4IG9mIHRoZSBwYXJhbWV0ZXIgZXN0aW1hdG9ycwokJApcaGF0e1xib2xkc3ltYm9se1xTaWdtYX19XjJfe1xoYXR7XGJvbGRzeW1ib2x7XGJldGF9fX0KPVxsZWZ0KFxtYXRoYmZ7WH1eVFxtYXRoYmZ7WH1ccmlnaHQpXnstMX1caGF0XHNpZ21hXjIKJCQKCnlvdSBjYW4gc2VlIHRoYXQgdGhlIHJhbmRvbWl6ZWQgY29tcGxldGUgYmxvY2sgd2lsbCBoYXZlIGFuIGltcGFjdCBvbgoKLSAkXGxlZnQoXG1hdGhiZntYfV5UXG1hdGhiZntYfVxyaWdodCleey0xfSQgYXMgd2VsbCBhcwotIG9uICRcc2lnbWFeMiQgb2YgdGhlIHJlc2lkdWFscyEKLS0+CgokXHJpZ2h0YXJyb3ckIFdlIHdlcmUgYWJsZSB0byBpc29sYXRlIHRoZSB2YXJpYW5jZSBpbiBleHByZXNzaW9uIGJldHdlZW4gYW5pbWFscy9ibG9ja3MgZnJvbSBvdXIgYW5hbHlzaXMhCgokXHJpZ2h0YXJyb3ckIFRoaXMgcmVkdWNlcyB0aGUgdmFyaWFuY2Ugb2YgdGhlIHJlc2lkdWFscyBhbmQgbGVhZHMgdG8gYSBwb3dlciBnYWluIGlmIHRoZSB2YXJpYWJpbGl0eSBiZXR3ZWVuIG1pY2UvYmxvY2tzIGlzIGxhcmdlLgoKQWxzbyBub3RlIHRoYXQsCgokJApcaGF0XHNpZ21hXjIgPSBcZnJhY3tcdGV4dHtTU0V9fXtuLXB9ID0gXGZyYWN7U1NUb3QgLSBTU00gLSBTU0NUfXtuLXB9CiQkCgotIEhlbmNlLCBibG9ja2luZyBpcyBiZW5lZmljaWFsIGlmIHRoZSByZWR1Y3Rpb24gaW4gc3VtIG9mIHNxdWFyZXMgb2YgdGhlIHJlc2lkdWFscyBpcyBsYXJnZSBjb21wYXJlZCB0byB0aGUgZGVncmVlcyBvZiBmcmVlZG9tIHRoYXQgYXJlIHNhY3JpZmljZWQuCi0gVGh1cyBpZiBTU00gY2FuIGV4cGxhaW4gYSBsYXJnZSBwYXJ0IG9mIHRoZSB0b3RhbCB2YXJpYWJpbGl0eS4KCkZ1cnRoZXIsIHRoZSBkZWdyZWVzIG9mIGZyZWVkb20gYWZmZWN0IHRoZSB0LWRpc3RyaWJ1dGlvbiB0aGF0IGlzIHVzZWQgZm9yIGluZmVyZW5jZSwgd2hpY2ggaGFzIGJyb2FkZXIgdGFpbHMgaWYgdGhlIHJlc2lkdWFsIGRlZ3JlZXMgb2YgZnJlZWRvbSAkbi1wJCBhcmUgZ2V0dGluZyBzbWFsbGVyLgoKIyBQb3dlciBnYWluIG9mIGFuIFJDQiB2cyBDUkQKCkluIHRoaXMgc2VjdGlvbiB3ZSB3aWxsIHN1YnNldCB0aGUgb3JpZ2luYWwgZGF0YSBpbiB0d28gZXhwZXJpbWVudHM6CgotIEEgcmFuZG9taXplZCBjb21wbGV0ZSBibG9jayBkZXNpZ24gd2l0aCB0aHJlZSBtaWNlCi0gQSBjb21wbGV0ZWx5IHJhbmRvbWl6ZWQgZGVzaWduIHdpdGggc2l4IG1pY2UgYnV0IHdoZXJlIHdlIG9ubHkgbWVhc3VyZSBvbmUgY2VsbCB0eXBlIGluIGVhY2ggbW91c2UuCgpgYGB7cn0Kc2V0LnNlZWQoODU5KQptUmNiIDwtIG1vdXNlICU+JQogIHB1bGwobW91c2UpICU+JQogIHVuaXF1ZSgpICU+JQogIHNhbXBsZShzaXplID0gMykKCnJjYlNtYWxsIDwtIG1vdXNlICU+JSBmaWx0ZXIobW91c2UgJWluJSBtUmNiKQpyY2JTbWFsbApgYGAKCmBgYHtyfQptQ3JkIDwtIG1vdXNlICU+JQogIHB1bGwobW91c2UpICU+JQogIHVuaXF1ZSgpICU+JQogIHNhbXBsZShzaXplID0gNikKCgpjcmRTbWFsbCA8LQogIGJpbmRfcm93cygKICAgIG1vdXNlICU+JQogICAgICBmaWx0ZXIobW91c2UgJWluJSBtQ3JkWzE6M10pICU+JQogICAgICBmaWx0ZXIoY2VsbHR5cGUgPT0gIlRjb24iKSwKICAgIG1vdXNlICU+JQogICAgICBmaWx0ZXIobW91c2UgJWluJSBtQ3JkWy0oMTozKV0pICU+JQogICAgICBmaWx0ZXIoY2VsbHR5cGUgPT0gIlRyZWciKQogICkKY3JkU21hbGwKYGBgCgpTbyBpbiBib3RoIGV4cGVyaW1lbnRzIHdlIG5lZWQgdG8gZG8gc2l4IG1hc3Mgc3BlY3Ryb21ldHJ5IHJ1bnMuCgoKYGBge3J9CmxtQ1JEU21hbGwgPC0gbG0oaW50ZW5zaXR5IH4gY2VsbHR5cGUsIGNyZFNtYWxsKQpzdW1tYXJ5KGxtQ1JEU21hbGwpCmFub3ZhKGxtQ1JEU21hbGwpCmBgYAoKYGBge3J9CmxtUkNCU21hbGwgPC0gbG0oaW50ZW5zaXR5IH4gY2VsbHR5cGUgKyBtb3VzZSwgcmNiU21hbGwpCmFub3ZhKGxtUkNCU21hbGwpCnN1bW1hcnkobG1SQ0JTbWFsbCkKYGBgCgoKTm90ZSwgdGhhdAoKLSB3ZSBhcmUgYWJsZSB0byBwaWNrIHVwIHRoZSB1cHJlZ3VsYXRpb24gYmV0d2VlbiByZWd1bGF0b3J5IFQtY2VsbHMgYW5kIG9yZGluYXJ5IFQtY2VsbHMgd2l0aCB0aGUgUkNCIGJ1dCBub3Qgd2l0aCB0aGUgQ1JELgotIHRoZSBzdGFuZGFyZCBlcnJvciBvZiB0aGUgJFxsb2dfMlx0ZXh0e0ZDfV9cdGV4dHtUcmVnLVRjb259JCBlc3RpbWF0ZSBpcyBhIGZhY3RvciBgciByb3VuZChzdW1tYXJ5KGxtQ1JEU21hbGwpJGNvZWZbImNlbGx0eXBlVHJlZyIsIlN0ZC4gRXJyb3IiXS9zdW1tYXJ5KGxtUkNCU21hbGwpJGNvZWZbImNlbGx0eXBlVHJlZyIsIlN0ZC4gRXJyb3IiXSwxKWAgc21hbGxlciBmb3IgdGhlIFJDQiBkZXNpZ24hCgpBIHBvb3IgZGF0YSBhbmFseXNpcyB3aG8gZm9yZ2V0cyBhYm91dCB0aGUgYmxvY2tpbmcgd2lsbCBiZSBiYWNrIGF0IHNxdWFyZSBvbmU6CgpgYGB7cn0Kd3JvbmdSYmMgPC0gbG0oaW50ZW5zaXR5IH4gY2VsbHR5cGUsIHJjYlNtYWxsKQphbm92YSh3cm9uZ1JiYykKc3VtbWFyeSh3cm9uZ1JiYykKYGBgCgpTbywgdGhlIGJsb2NrIHRvIGJsb2NrIHZhcmlhYmlsaXR5IGlzIHRoZW4gYWJzb3JiZWQgaW4gdGhlIHZhcmlhbmNlIGVzdGltYXRvciBvZiB0aGUgcmVzaWR1YWwuCgpPZiBjb3Vyc2UsIHdlIGFyZSBuZXZlciBhbGxvd2VkIHRvIGFuYWx5c2UgYW4gUkNCIHdpdGggYSBtb2RlbCBmb3IgYSBDUkQgKHdpdGhvdXQgYmxvY2sgZmFjdG9yKSBiZWNhdXNlIGJsb2NraW5nIGltcG9zZXMgYSByYW5kb21pemF0aW9uIHJlc3RyaWN0aW9uOiB3ZSByYW5kb21pemUgdGhlIHRyZWF0bWVudCB3aXRoaW4gYmxvY2suCgojIyBQb3dlciBnYWluIG9mIGJsb2NraW5nPwoKIyMjIFBvd2VyIGZvciBjb21wbGV0ZWx5IHJhbmRvbWl6ZWQgZGVzaWduCgpgYGB7cn0KdmFyQmV0d2VlblBsdXNXaXRoaW4gPC0gc3VtKGNhcjo6QW5vdmEobG1SQ0IsIHR5cGUgPSAiSUlJIilbYygibW91c2UiLCAiUmVzaWR1YWxzIiksICJTdW0gU3EiXSkgLyBzdW0oY2FyOjpBbm92YShsbVJDQiwgdHlwZSA9ICJJSUkiKVtjKCJtb3VzZSIsICJSZXNpZHVhbHMiKSwgIkRmIl0pCgphbHBoYSA8LSAwLjA1Cm5TaW0gPC0gMjAwMDAKYjAgPC0gMApzZCA8LSBzcXJ0KHZhckJldHdlZW5QbHVzV2l0aGluKQpucyA8LSBjKDMsIDcpCmRlbHRhcyA8LSBsbVJDQiRjb2VmZmljaWVudHNbImNlbGx0eXBlVHJlZyJdCgpMIDwtIGxpbW1hOjptYWtlQ29udHJhc3RzKCJjZWxsdHlwZVRyZWciLCBsZXZlbHMgPSBjKCIoSW50ZXJjZXB0KSIsICJjZWxsdHlwZVRyZWciKSkKCnBvd2VyRmFzdCA8LSBtYXRyaXgoTkEsIG5yb3cgPSBsZW5ndGgobnMpICogbGVuZ3RoKGRlbHRhcyksIG5jb2wgPSAzKSAlPiUgYXMuZGF0YS5mcmFtZSgpCm5hbWVzKHBvd2VyRmFzdCkgPC0gYygiYjEiLCAibiIsICJwb3dlciIpCgppIDwtIDAKZm9yIChuIGluIG5zKQp7CiAgbjEgPC0gbjIgPC0gbgoKICAjIyMgU2ltdWxhdGlvbgogIHByZWRpY3RvckRhdGEgPC0gZGF0YS5mcmFtZShjZWxsdHlwZSA9IHJlcChjKCJUY29uIiwgIlRyZWciKSwgYyhuMSwgbjIpKSAlPiUgYXMuZmFjdG9yKCkpCiAgZGVzaWduIDwtIG1vZGVsLm1hdHJpeCh+Y2VsbHR5cGUsIHByZWRpY3RvckRhdGEpCgogIGZvciAoYjEgaW4gZGVsdGFzKQogIHsKICAgIHlTaW0gPC0gcm5vcm0obnJvdyhwcmVkaWN0b3JEYXRhKSAqIG5TaW0sIHNkID0gc2QpCiAgICBkaW0oeVNpbSkgPC0gYyhucm93KHByZWRpY3RvckRhdGEpLCBuU2ltKQogICAgeVNpbSA8LSB5U2ltICsgYyhkZXNpZ24gJSolIGMoYjAsIGIxKSkKICAgIHlTaW0gPC0gdCh5U2ltKQoKICAgICMjIyBGaXR0aW5nCiAgICBmaXRBbGwgPC0gbGltbWE6OmxtRml0KHlTaW0sIGRlc2lnbikKCiAgICAjIyMgSW5mZXJlbmNlCiAgICB2YXJVbnNjYWxlZCA8LSBjKHQoTCkgJSolIGZpdEFsbCRjb3YuY29lZmZpY2llbnRzICUqJSBMKQogICAgY29udHJhc3RzIDwtIGZpdEFsbCRjb2VmZmljaWVudHMgJSolIEwKICAgIHNlQ29udHJhc3RzIDwtIHZhclVuc2NhbGVkXi41ICogZml0QWxsJHNpZ21hCiAgICB0c3RhdHMgPC0gY29udHJhc3RzIC8gc2VDb250cmFzdHMKICAgIHB2YWxzIDwtIHB0KGFicyh0c3RhdHMpLCBmaXRBbGwkZGYucmVzaWR1YWwsIGxvd2VyLnRhaWwgPSBGQUxTRSkgKiAyCgogICAgaSA8LSBpICsgMQogICAgcG93ZXJGYXN0W2ksIF0gPC0gYyhiMSwgbiwgbWVhbihwdmFscyA8IGFscGhhKSkKICB9Cn0KcG93ZXJGYXN0CmBgYAoKQmVjYXVzZSB3ZSBoYXZlIGEgc2ltcGxlIDIgZ3JvdXAgY29tcGFyaXNvbiB3ZSBjYW4gYWxzbyBjYWxjdWxhdGUgdGhlIHBvd2VyIHVzaW5nIHRoZSAgYHBvd2VyLnQudGVzdGAgZnVuY3Rpb24uCgpgYGB7cn0KcG93ZXIudC50ZXN0KG4gPSAzLCBkZWx0YSA9IGxtUkNCJGNvZWZmaWNpZW50c1siY2VsbHR5cGVUcmVnIl0sIHNkID0gc3FydCh2YXJCZXR3ZWVuUGx1c1dpdGhpbikpCnBvd2VyLnQudGVzdChuID0gNywgZGVsdGEgPSBsbVJDQiRjb2VmZmljaWVudHNbImNlbGx0eXBlVHJlZyJdLCBzZCA9IHNxcnQodmFyQmV0d2VlblBsdXNXaXRoaW4pKQpgYGAKCiMjIFBvd2VyIGZvciByYW5kb21pemVkIGNvbXBsZXRlIGJsb2NrIGRlc2lnbgoKCgoKYGBge3J9CmFscGhhIDwtIDAuMDUKblNpbSA8LSAyMDAwMApiMCA8LSAwCnNkIDwtIHNpZ21hKGxtUkNCKQpzZE1vdXNlIDwtIHNxcnQoY2FyOjpBbm92YShsbVJDQilbIm1vdXNlIiwgIlN1bSBTcSJdIC8gY2FyOjpBbm92YShsbVJDQilbIm1vdXNlIiwgIkRmIl0pCm5zIDwtIGMoMywgNykKZGVsdGFzIDwtIGxtUkNCJGNvZWZmaWNpZW50c1siY2VsbHR5cGVUcmVnIl0KCgpwb3dlckZhc3RCbG9ja2luZyA8LSBtYXRyaXgoTkEsIG5yb3cgPSBsZW5ndGgobnMpICogbGVuZ3RoKGRlbHRhcyksIG5jb2wgPSAzKSAlPiUgYXMuZGF0YS5mcmFtZSgpCm5hbWVzKHBvd2VyRmFzdEJsb2NraW5nKSA8LSBjKCJiMSIsICJuIiwgInBvd2VyIikKCmkgPC0gMApmb3IgKG4gaW4gbnMpCnsKCiAgIyMjIFNpbXVsYXRpb24KICBwcmVkaWN0b3JEYXRhIDwtIGRhdGEuZnJhbWUoY2VsbHR5cGUgPSByZXAoYygiVGNvbiIsICJUcmVnIiksIGVhY2ggPSBuKSAlPiUgYXMuZmFjdG9yKCksIG1vdXNlID0gcGFzdGUwKCJtIiwgcmVwKDE6biwgMikpKQogIGRlc2lnbiA8LSBtb2RlbC5tYXRyaXgofiBjZWxsdHlwZSArIG1vdXNlLCBwcmVkaWN0b3JEYXRhKQogIEwgPC0gbGltbWE6Om1ha2VDb250cmFzdHMoImNlbGx0eXBlVHJlZyIsIGxldmVscyA9IGNvbG5hbWVzKGRlc2lnbikpCgogIGZvciAoYjEgaW4gZGVsdGFzKQogIHsKICAgIHlTaW0gPC0gcm5vcm0obnJvdyhwcmVkaWN0b3JEYXRhKSAqIG5TaW0sIHNkID0gc2QpCiAgICBkaW0oeVNpbSkgPC0gYyhucm93KHByZWRpY3RvckRhdGEpLCBuU2ltKQogICAgbW91c2VFZmZlY3QgPC0gcm5vcm0obiwgc2QgPSBzZE1vdXNlKQogICAgYmV0YXNNb3VzZSA8LSBtb3VzZUVmZmVjdFstMV0gLSBtb3VzZUVmZmVjdFsxXQogICAgeVNpbSA8LSB5U2ltICsgYyhkZXNpZ24gJSolIGMoYjAsIGIxLCBiZXRhc01vdXNlKSkKICAgIHlTaW0gPC0gdCh5U2ltKQoKICAgICMjIyBGaXR0aW5nCiAgICBmaXRBbGwgPC0gbGltbWE6OmxtRml0KHlTaW0sIGRlc2lnbikKCiAgICAjIyMgSW5mZXJlbmNlCiAgICB2YXJVbnNjYWxlZCA8LSBjKHQoTCkgJSolIGZpdEFsbCRjb3YuY29lZmZpY2llbnRzICUqJSBMKQogICAgY29udHJhc3RzIDwtIGZpdEFsbCRjb2VmZmljaWVudHMgJSolIEwKICAgIHNlQ29udHJhc3RzIDwtIHZhclVuc2NhbGVkXi41ICogZml0QWxsJHNpZ21hCiAgICB0c3RhdHMgPC0gY29udHJhc3RzIC8gc2VDb250cmFzdHMKICAgIHB2YWxzIDwtIHB0KGFicyh0c3RhdHMpLCBmaXRBbGwkZGYucmVzaWR1YWwsIGxvd2VyLnRhaWwgPSBGQUxTRSkgKiAyCgogICAgaSA8LSBpICsgMQogICAgcG93ZXJGYXN0QmxvY2tpbmdbaSwgXSA8LSBjKGIxLCBuLCBtZWFuKHB2YWxzIDwgYWxwaGEpKQogIH0KfQpwb3dlckZhc3RCbG9ja2luZwpgYGAKCk5vdGUsIHRoYXQgdGhlIHBvd2VyIGlzIGluZGVlZCBtdWNoIGxhcmdlciBmb3IgdGhlIHJhbmRvbWl6ZWQgY29tcGxldGUgYmxvY2sgZGVzaWduLgpCb3RoIGZvciB0aGUgZGVzaWducyB3aXRoIDYgYW5kIDE0IG1hc3Mgc3BlY3Ryb21ldGVyIHJ1bnMuCgpCZWNhdXNlIHdlIGhhdmUgYW4gUkNCIHdpdGggYSBibG9jayBzaXplIG9mIDIgKHBhaXJlZCBkZXNpZ24pIHdlIGNhbiBhbHNvIGNhbGN1bGF0ZSB0aGUgcG93ZXIgdXNpbmcgdGhlIGBwb3dlci50LnRlc3QgZnVuY3Rpb25gIHdpdGggYHR5cGUgPSAib25lLnNhbXBsZSJgIGFuZCBgc2RgIGVxdWFsIHRvIHRoZSBzdGFuZGFyZCBkZXZpYXRpb24gb2YgdGhlIGRpZmZlcmVuY2UuCgoKYGBge3J9CnBvd2VyLnQudGVzdChuID0gMywgZGVsdGEgPSBtZWFuKG1vdXNlV2lkZSRkZWx0YSksIHNkID0gc2QobW91c2VXaWRlJGRlbHRhKSkKcG93ZXIudC50ZXN0KG4gPSA3LCBkZWx0YSA9IG1lYW4obW91c2VXaWRlJGRlbHRhKSwgc2QgPSBzZChtb3VzZVdpZGUkZGVsdGEpKQpgYGAKCk5vdGUsIHRoYXQgdGhlIHBvd2VyIGlzIHNsaWdodGx5IGRpZmZlcmVudCBiZWNhdXNlIGZvciB0aGUgcG93ZXIudC50ZXN0IGZ1bmN0aW9uIHdlIGNvbmRpdGlvbmVkIG9uIHRoZSBtaWNlIGZyb20gb3VyIHN0dWR5LiBXaGlsZSBpbiB0aGUgc2ltdWxhdGlvbiBzdHVkeSB3ZSBnZW5lcmF0ZWQgZGF0YSBmb3IgbmV3IG1pY2UgYnkgc2ltdWxhdGluZyB0aGUgbW91c2UgZWZmZWN0IGZyb20gYSBub3JtYWwgZGlzdHJpYnV0aW9uLgoKIyMgSW1wYWN0IG9mIHRoZSBhbW91bnQgb2YgdmFyaWFiaWxpdHkgdGhhdCB0aGUgYmxvY2tpbmcgZmFjdG9yIGV4cGxhaW5zIG9uIHRoZSBwb3dlcj8KCldlIHdpbGwgdmFyeSB0aGUgYmxvY2sgZWZmZWN0IGV4cGxhaW5zCiQkClxmcmFje1xzaWdtYV4yX1x0ZXh0e2JldHdlZW59fXtcc2lnbWFeMl9cdGV4dHtiZXR3ZWVufStcc2lnbWFeMl9cdGV4dHt3aXRoaW59fT0xLVxmcmFje1xzaWdtYV4yX1x0ZXh0e3dpdGhpbn19e1xzaWdtYV4yX1x0ZXh0e2JldHdlZW59K1xzaWdtYV4yX1x0ZXh0e3dpdGhpbn19CiQkClNvIGluIG91ciBleGFtcGxlIHRoYXQgaXMgdGhlIHJhdGlvIGJldHdlZW4gdGhlIHZhcmlhYmlsaXR5IGJldHdlZW4gdGhlIG1pY2UgYW5kIHRoZSBzdW0gb2YgdGhlIHZhcmlhYmlsaXR5IGJldHdlZW4gYW5kIHdpdGhpbiB0aGUgbWljZS4gTm90ZSwgdGhhdCB0aGUgd2l0aGluIG1vdXNlIHZhcmlhYmlsaXR5IHdhcyB0aGUgdmFyaWFuY2Ugb2YgdGhlIGVycm9ycyBvZiB0aGUgUkNCLiBUaGUgcmF0aW8gZm9yIG91ciBleHBlcmltZW50IGVxdWFscwoKYGBge3J9CnZhckJldHdlZW5QbHVzV2l0aGluIDwtIHN1bShjYXI6OkFub3ZhKGxtUkNCLCB0eXBlID0gIklJSSIpW2MoIm1vdXNlIiwgIlJlc2lkdWFscyIpLCAiU3VtIFNxIl0pIC8gc3VtKGNhcjo6QW5vdmEobG1SQ0IsIHR5cGUgPSAiSUlJIilbYygibW91c2UiLCAiUmVzaWR1YWxzIiksICJEZiJdKQp2YXJXaXRoaW4gPC0gY2FyOjpBbm92YShsbVJDQilbIlJlc2lkdWFscyIsICJTdW0gU3EiXSAvIGNhcjo6QW5vdmEobG1SQ0IpWyJSZXNpZHVhbHMiLCAiRGYiXQp2YXJCZXR3ZWVuUGx1c1dpdGhpbgp2YXJXaXRoaW4KMSAtIHZhcldpdGhpbiAvIHZhckJldHdlZW5QbHVzV2l0aGluCmBgYAoKCmBgYHtyfQphbHBoYSA8LSAwLjA1Cm5TaW0gPC0gMjAwMDAKYjAgPC0gMAp2YXJCZXR3ZWVuUGx1c1dpdGhpbiA8LSBzdW0oY2FyOjpBbm92YShsbVJDQiwgdHlwZSA9ICJJSUkiKVtjKCJtb3VzZSIsICJSZXNpZHVhbHMiKSwgIlN1bSBTcSJdKSAvIHN1bShjYXI6OkFub3ZhKGxtUkNCLCB0eXBlID0gIklJSSIpW2MoIm1vdXNlIiwgIlJlc2lkdWFscyIpLCAiRGYiXSkKCgpucyA8LSBjKDMsIDcpCmRlbHRhcyA8LSBsbVJDQiRjb2VmZmljaWVudHNbImNlbGx0eXBlVHJlZyJdCgpmcmFjVmFycyA8LSBzZXEoMCwgLjk1LCAuMDUpCgpwb3dlckZhc3RCbG9ja2luZ0xvdyA8LSBtYXRyaXgoTkEsIG5yb3cgPSBsZW5ndGgobnMpICogbGVuZ3RoKGZyYWNWYXJzKSwgbmNvbCA9IDMpICU+JSBhcy5kYXRhLmZyYW1lKCkKbmFtZXMocG93ZXJGYXN0QmxvY2tpbmdMb3cpIDwtIGMoImZyYWNWYXJzIiwgIm4iLCAicG93ZXIiKQoKaSA8LSAwCgoKZm9yIChuIGluIG5zKQp7CgogICMjIyBTaW11bGF0aW9uCiAgcHJlZGljdG9yRGF0YSA8LSBkYXRhLmZyYW1lKGNlbGx0eXBlID0gcmVwKGMoIlRjb24iLCAiVHJlZyIpLCBlYWNoID0gbikgJT4lIGFzLmZhY3RvcigpLCBtb3VzZSA9IHBhc3RlMCgibSIsIHJlcCgxOm4sIDIpKSkKICBkZXNpZ24gPC0gbW9kZWwubWF0cml4KH4gY2VsbHR5cGUgKyBtb3VzZSwgcHJlZGljdG9yRGF0YSkKICBMIDwtIGxpbW1hOjptYWtlQ29udHJhc3RzKCJjZWxsdHlwZVRyZWciLCBsZXZlbHMgPSBjb2xuYW1lcyhkZXNpZ24pKQogIGZvciAoZnJhY1ZhciBpbiBmcmFjVmFycykKICB7CiAgICBzZCA8LSBzcXJ0KHZhckJldHdlZW5QbHVzV2l0aGluICogKDEgLSBmcmFjVmFyKSkKICAgIHNkTW91c2UgPC0gc3FydCh2YXJCZXR3ZWVuUGx1c1dpdGhpbiAqIGZyYWNWYXIpCiAgICBmb3IgKGIxIGluIGRlbHRhcykKICAgIHsKICAgICAgeVNpbSA8LSBybm9ybShucm93KHByZWRpY3RvckRhdGEpICogblNpbSwgc2QgPSBzZCkKICAgICAgZGltKHlTaW0pIDwtIGMobnJvdyhwcmVkaWN0b3JEYXRhKSwgblNpbSkKICAgICAgbW91c2VFZmZlY3QgPC0gcm5vcm0obiwgc2QgPSBzZE1vdXNlKQogICAgICBiZXRhc01vdXNlIDwtIG1vdXNlRWZmZWN0Wy0xXSAtIG1vdXNlRWZmZWN0WzFdCiAgICAgIHlTaW0gPC0geVNpbSArIGMoZGVzaWduICUqJSBjKGIwLCBiMSwgYmV0YXNNb3VzZSkpCiAgICAgIHlTaW0gPC0gdCh5U2ltKQoKICAgICAgIyMjIEZpdHRpbmcKICAgICAgZml0QWxsIDwtIGxpbW1hOjpsbUZpdCh5U2ltLCBkZXNpZ24pCgogICAgICAjIyMgSW5mZXJlbmNlCiAgICAgIHZhclVuc2NhbGVkIDwtIGModChMKSAlKiUgZml0QWxsJGNvdi5jb2VmZmljaWVudHMgJSolIEwpCiAgICAgIGNvbnRyYXN0cyA8LSBmaXRBbGwkY29lZmZpY2llbnRzICUqJSBMCiAgICAgIHNlQ29udHJhc3RzIDwtIHZhclVuc2NhbGVkXi41ICogZml0QWxsJHNpZ21hCiAgICAgIHRzdGF0cyA8LSBjb250cmFzdHMgLyBzZUNvbnRyYXN0cwogICAgICBwdmFscyA8LSBwdChhYnModHN0YXRzKSwgZml0QWxsJGRmLnJlc2lkdWFsLCBsb3dlci50YWlsID0gRkFMU0UpICogMgoKICAgICAgaSA8LSBpICsgMQogICAgICBwb3dlckZhc3RCbG9ja2luZ0xvd1tpLCBdIDwtIGMoZnJhY1ZhciwgbiwgbWVhbihwdmFscyA8IGFscGhhKSkKICAgIH0KICB9Cn0KcG93ZXJGYXN0QmxvY2tpbmdMb3cKYGBgCgpgYGB7cn0KZ2dfY29sb3JfaHVlIDwtIGZ1bmN0aW9uKG4pIHsKICBodWVzIDwtIHNlcSgxNSwgMzc1LCBsZW5ndGggPSBuICsgMSkKICBoY2woaCA9IGh1ZXMsIGwgPSA2NSwgYyA9IDEwMClbMTpuXQp9CmNvbHMgPC0gZ2dfY29sb3JfaHVlKDIpCgpwb3dlckZhc3RCbG9ja2luZ0xvdyAlPiUKICBhcy5kYXRhLmZyYW1lKCkgJT4lCiAgbXV0YXRlKG4gPSBhcy5mYWN0b3IobikpICU+JQogIGdncGxvdChhZXMoZnJhY1ZhcnMsIHBvd2VyLCBncm91cCA9IG4sIGNvbG9yID0gbikpICsKICBnZW9tX2xpbmUoKSArCiAgZ2VvbV9obGluZSh5aW50ZXJjZXB0ID0gcG93ZXJGYXN0ICU+JSBmaWx0ZXIobiA9PSAzKSAlPiUgcHVsbChwb3dlciksIGNvbG9yID0gY29sc1sxXSkgKwogIGFubm90YXRlKCJ0ZXh0IiwKICAgIGxhYmVsID0gIkNSRCAobj0zKSIsCiAgICB4ID0gMC4wNSwgeSA9IHBvd2VyRmFzdCAlPiUgZmlsdGVyKG4gPT0gMykgJT4lIHB1bGwocG93ZXIpICsgLjAyLCBzaXplID0gMywgY29sb3VyID0gY29sc1sxXQogICkgKwogIGdlb21faGxpbmUoeWludGVyY2VwdCA9IHBvd2VyRmFzdCAlPiUgZmlsdGVyKG4gPT0gNykgJT4lIHB1bGwocG93ZXIpLCBjb2xvciA9IGNvbHNbMl0pICsKICBhbm5vdGF0ZSgidGV4dCIsCiAgICBsYWJlbCA9ICJDUkQgKG49NykiLAogICAgeCA9IDAuMDUsIHkgPSBwb3dlckZhc3QgJT4lIGZpbHRlcihuID09IDcpICU+JSBwdWxsKHBvd2VyKSArIC4wMiwgc2l6ZSA9IDMsIGNvbG91ciA9IGNvbHNbMl0KICApICsKICB4bGFiKGV4cHJlc3Npb24ofiBzaWdtYVtiZXR3ZWVuXV4yIC8gKHNpZ21hW2JldHdlZW5dXjIgKyBzaWdtYVt3aXRoaW5dXjIpKSkgKwogIGdlb21fdmxpbmUoeGludGVyY2VwdCA9IDEgLSB2YXJXaXRoaW4gLyB2YXJCZXR3ZWVuUGx1c1dpdGhpbikgKwogIHhsaW0oMCwgMSkKYGBgCgotIFNvIGlmIHRoZSB2YXJpYW5jZSB0aGF0IGlzIGV4cGxhaW5lZCBieSB0aGUgYmxvY2sgZWZmZWN0IGlzIHNtYWxsIHlvdSB3aWxsIGxvb3NlIHBvd2VyIGFzIGNvbXBhcmVkIHRvIHRoZSBhbmFseXNpcyB3aXRoIGEgQ1JEIGRlc2lnbi4gSW5kZWVkLCB0aGVuCgogICAgLSBTU0UgZG9lcyBub3QgcmVkdWNlIG11Y2ggYW5kCiAgICAtIG4kX1x0ZXh0e2Jsb2Nrc30kLTEgZGVncmVlcyBvZiBmcmVlZG9tIGhhdmUgYmVlbiBzYWNyaWZpY2VkLgoKLSBBcyBzb29uIGFzIHRoZSBibG9jayBlZmZlY3QgZXhwbGFpbnMgYSBsYXJnZSBwYXJ0IG9mIHRoZSB2YXJpYWJpbGl0eSBpdCBpcyB2ZXJ5IGJlbmVmaWNpYWwgdG8gdXNlIGEgcmFuZG9taXplZCBjb21wbGV0ZSBibG9jayBkZXNpZ24hCgotIE5vdGUsIHRoYXQgdGhlIHNhbWUgbnVtYmVyIG9mIG1hc3Mgc3BlY3Ryb21ldHJ5IHJ1bnMgaGF2ZSB0byBiZSBkb25lIGZvciBib3RoIHRoZSBSQ0IgYW5kIENSRCBkZXNpZ24uIEhvd2V2ZXIsIGZvciB0aGUgUkNCIHdlIG9ubHkgbmVlZCBoYWxmIG9mIHRoZSBtaWNlLgoKIyBQZW5pY2lsbGluIGV4YW1wbGUKClRoZSBwcm9kdWN0aW9uIG9mIHBlbmljaWxsaW4gY29ybiBzdGVlcCBsaXF1b3IgaXMgdXNlZC4gQ29ybiBzdGVlcCBsaXF1b3IgaXMgcHJvZHVjZWQgaW4gYmxlbmRzIGFuZCB0aGVyZSBpcyBhIGNvbnNpZGVyYWJsZSB2YXJpYWJpbGl0eSBiZXR3ZWVuIHRoZSBibGVuZHMuIFN1cHBvc2UgdGhhdAoKLSBmb3VyIGNvbXBldGluZyBtZXRob2RzIGhhdmUgdG8gYmUgZXZhbHVhdGVkIHRvIHByb2R1Y2UgcGVuaWNpbGxpbiAoQS1EKSwKLSBvbmUgYmxlbmRzIGlzIHN1ZmZpY2llbnQgZm9yIGZvdXIgcnVucyBvZiBhIHBlbmljaWxsaW4gYmF0Y2ggcmVhY3RvciBhbmQKLSB0aGUgMjAgcnVucyBjYW4gYmUgc2NoZWR1bGVkIGZvciB0aGUgZXhwZXJpbWVudC4KCkhvdyB3b3VsZCB5b3UgYXNzaWduIHRoZSBtZXRob2RzIHRvIHRoZSBibGVuZHMuCgpgYGB7cn0KZGF0YShwZW5pY2lsbGluLCBwYWNrYWdlID0gImZhcmF3YXkiKQp0YWJsZShwZW5pY2lsbGluJGJsZW5kLCBwZW5pY2lsbGluJHRyZWF0KQpgYGAKCiMjIERhdGEKCmBgYHtyfQpoZWFkKHBlbmljaWxsaW4pCm1hdHJpeChwZW5pY2lsbGluJHlpZWxkLCBucm93ID0gNSwgbmNvbCA9IDQsIGJ5cm93ID0gVFJVRSwgZGltbmFtZXMgPSBsaXN0KGxldmVscyhwZW5pY2lsbGluJGJsZW5kKSwgbGV2ZWxzKHBlbmljaWxsaW4kdHJlYXQpKSkKYGBgCgpgYGB7cn0KcGVuaWNpbGxpbiAlPiUKICBnZ3Bsb3QoYWVzKHggPSBibGVuZCwgeSA9IHlpZWxkLCBncm91cCA9IHRyZWF0LCBjb2xvciA9IHRyZWF0KSkgKwogIGdlb21fbGluZSgpICsKICBnZW9tX3BvaW50KCkKYGBgCgpgYGB7cn0KcGVuaWNpbGxpbiAlPiUKICBnZ3Bsb3QoYWVzKHggPSB0cmVhdCwgeSA9IHlpZWxkLCBncm91cCA9IGJsZW5kLCBjb2xvciA9IGJsZW5kKSkgKwogIGdlb21fbGluZSgpICsKICBnZW9tX3BvaW50KCkKYGBgCgojIyBBbmFseXNpcwoKV2UgYW5hbHlzZSB0aGUgeWllbGQgdXNpbmcKCi0gYSBmYWN0b3IgZm9yIGJsZW5kIGFuZAotIGEgZmFjdG9yIGZvciB0cmVhdG1lbnQuCgpgYGB7cn0KbG1QZW4gPC0gbG0oeWllbGQgfiB0cmVhdCArIGJsZW5kLCBkYXRhID0gcGVuaWNpbGxpbikKcGxvdChsbVBlbikKY2FyOjpBbm92YShsbVBlbiwgdHlwZSA9ICJJSUkiKQpgYGAKCldlIGNvbmNsdWRlIHRoYXQgdGhlIGVmZmVjdCBvZiB0aGUgdHJlYXRtZW50IG9uIHRoZSBwZW5pY2lsbGluIHlpZWxkIGlzIG5vdCBzaWduaWZpY2FudCBhdCB0aGUgNSUgbGV2ZWwgb2Ygc2lnbmlmaWNhbmNlIChwID0gYHIgY2FyOjpBbm92YShsbVBlbix0eXBlPSJJSUkiKVsidHJlYXQiLCJQcig+RikiXSAlPiUgcm91bmQoLiwyKWAuCgpXZSBhbHNvIG9ic2VydmUgdGhhdCB0aGVyZSBpcyBhIGxhcmdlIGVmZmVjdCBvZiB0aGUgYmxlbmQgb24gdGhlIHlpZWxkLgpCbGVuZCBleHBsYWlucyBhYm91dCBgciByb3VuZChjYXI6OkFub3ZhKGxtUGVuLHR5cGU9IklJSSIpWyJibGVuZCIsIlN1bSBTcSJdL3N1bShjYXI6OkFub3ZhKGxtUGVuLHR5cGU9IklJSSIpWy0xLCJTdW0gU3EiXSkqMTAwLDEpYCUgb2YgdGhlIHZhcmlhYmlsaXR5IGluIHRoZSBwZW5pY2lsbGluIHlpZWxkLgoKCiMgUHNldWRvLXJlcGxpY2F0aW9uCgpBIHN0dWR5IG9uIHRoZSBmYWN1bHRhdGl2ZSBwYXRob2dlbiBGcmFuY2lzZWxsYSB0dWxhcmVuc2lzIHdhcyBjb25jZWl2ZWQgYnkgUmFtb25kIGV0IGFsLiAoMjAxNSkgWzEyXS4KCi0gRi4gdHVsYXJlbnNpcyBlbnRlcnMgdGhlIGNlbGxzIG9mIGl0cyBob3N0IGJ5IHBoYWdvY3l0b3Npcy4KLSBUaGUgYXV0aG9ycyBzaG93ZWQgdGhhdCBGLiB0dWxhcmVuc2lzIGlzIGFyZ2luaW5lIGRlZmljaWVudCBhbmQgaW1wb3J0cyBhcmdpbmluZSBmcm9tIHRoZSBob3N0IGNlbGwgdmlhIGFuIGFyZ2luaW5lIHRyYW5zcG9ydGVyLCBBcmdQLCBpbiBvcmRlciB0byBlZmZpY2llbnRseSBlc2NhcGUgZnJvbSB0aGUgcGhhZ29zb21lIGFuZCByZWFjaCB0aGUgY3l0b3NvbGljIGNvbXBhcnRtZW50LCB3aGVyZSBpdCBjYW4gYWN0aXZlbHkgbXVsdGlwbHkuCi0gSW4gdGhlaXIgc3R1ZHksIHRoZXkgY29tcGFyZWQgdGhlIHByb3Rlb21lIG9mIHdpbGQgdHlwZSBGLiB0dWxhcmVuc2lzIChXVCkgdG8gQXJnUC1nZW5lIGRlbGV0ZWQgRi4gdHVsYXJlbnNpcyAoa25vY2stb3V0LCBEOCkuCgotIFRoZSBzYW1wbGUgZm9yIGVhY2ggYmlvLXJlcCB3YXMgcnVuIGluIHRlY2huaWNhbCB0cmlwbGljYXRlIG9uIHRoZSBtYXNzLXNwZWN0cm9tZXRlci4KCi0gV2Ugd2lsbCB1c2UgZGF0YSBmb3IgdGhlIHByb3RlaW4gNTBTIHJpYm9zb21hbCBwcm90ZWluIEw1IFtBMFE0SjVdKGh0dHBzOi8vd3d3LnVuaXByb3Qub3JnL3VuaXByb3QvQTBRNEo1KQoKIyMgRGF0YSBleHBsb3JhdGlvbgoKYGBge3J9CmZyYW5jIDwtIHJlYWRfdHN2KCJodHRwczovL3Jhdy5naXRodWJ1c2VyY29udGVudC5jb20vc3RhdE9taWNzL1BTTFNEYXRhL21haW4vZnJhbmNpc2VsbGFBMFE0SjUudHh0IikKZnJhbmMKYGBgCgpgYGB7cn0KZnJhbmMgJT4lCiAgZ2dwbG90KGFlcyhiaW9yZXAsIGludGVuc2l0eUxvZzIsIGNvbG9yID0gZ2Vub3R5cGUpKSArCiAgZ2VvbV9wb2ludCgpCmBgYAoKLSBSZXNwb25zZT8KLSBFeHBlcmltZW50YWwgdW5pdD8KLSBPYnNlcnZhdGlvbmFsIHVuaXQ/Ci0gRmFjdG9ycz8KCiRccmlnaHRhcnJvdyQgUHNldWRvLXJlcGxpY2F0aW9uLCByYW5kb21pc2F0aW9uIHRvIGJpby1yZXBlYXQgYW5kIGVhY2ggYmlvLXJlcGVhdCBtZWFzdXJlZCBpbiB0ZWNobmljYWwgdHJpcGxpY2F0ZS4KJFxyaWdodGFycm93JCBJZiB3ZSB3b3VsZCBhbmFseXNlIHRoZSBkYXRhIHVzaW5nIGEgbGluZWFyIG1vZGVsIGJhc2VkIG9uIGVhY2ggbWVhc3VyZWQgaW50ZW5zaXR5LCB3ZSB3b3VsZCBhY3QgYXMgaWYgd2UgaGFkIHNhbXBsZWQgMTggYmlvLXJlcGVhdHMuCiRccmlnaHRhcnJvdyQgRWZmZWN0IG9mIGludGVyZXN0IGhhcyB0byBiZSBhc3Nlc3NlZCBiZXR3ZWVuIGJpby1yZXBlYXRzLiBTbyBibG9jayBhbmFseXNpcyBub3QgcG9zc2libGUhCgpJZiB0aGUgc2FtZSBudW1iZXIgb2YgcHNldWRvLXJlcGxpY2F0ZXMvdGVjaG5pY2FsIHJlcGxpY2F0ZXMgYXJlIGF2YWlsYWJsZSBmb3IgZWFjaCBiaW8tcmVwZWF0OgoKLSBhdmVyYWdlIGZpcnN0IG92ZXIgYmlvLXJlcGVhdHMgdG8gb2J0YWluIGluZGVwZW5kZW50IG1lYXN1cmVtZW50cwotIGF2ZXJhZ2VzIHdpbGwgdGhlbiBoYXZlIHRoZSBzYW1lIHByZWNpc2lvbgotIGFzc2VzcyBlZmZlY3Qgb2YgdHJlYXRtZW50IHVzaW5nIGF2ZXJhZ2VzCi0gKipDYXV0aW9uOiBuZXZlciBzdW1tYXJpemUgb3ZlciBiaW8tcmVwZWF0cy9leHBlcmltZW50YWwgdW5pdHMqKgoKCmBgYHtyfQpsbUJpb3JlcCA8LSBsbShpbnRlbnNpdHlMb2cyIH4gLTEgKyBiaW9yZXAsIGZyYW5jKQpsbUJpb3JlcApgYGAKCmBgYHtyfQpmcmFuY1N1bSA8LSBkYXRhLmZyYW1lKGdlbm90eXBlID0gcmVwKGMoIkQ4IiwgIldUIiksIGVhY2ggPSAzKSAlPiUgYXMuZmFjdG9yKCkgJT4lIHJlbGV2ZWwoIldUIiksIGludGVuc2l0eUxvZzIgPSBsbUJpb3JlcCRjb2VmKQpmcmFuY1N1bQpgYGAKCmBgYHtyfQpsbVN1bSA8LSBsbShpbnRlbnNpdHlMb2cyIH4gZ2Vub3R5cGUsIGZyYW5jU3VtKQpzdW1tYXJ5KGxtU3VtKQpgYGAKCiMjIFdyb25nIGFuYWx5c2lzCgpgYGB7cn0KbG1Xcm9uZyA8LSBsbShpbnRlbnNpdHlMb2cyIH4gZ2Vub3R5cGUsIGZyYW5jKQpzdW1tYXJ5KGxtV3JvbmcpCmBgYAoKTm90ZSwgdGhhdCB0aGUgYW5hbHlzaXMgd2hlcmUgd2UgaWdub3JlIHRoYXQgd2UgaGF2ZSBtdWx0aXBsZSB0ZWNobmljYWwgcmVwZWF0cyBmb3IgZWFjaCBiaW8tcmVwZWF0IHJldHVybnMgcmVzdWx0cyB0aGF0IGFyZSBtdWNoIG1vcmUgc2lnbmlmaWNhbnQgYmVjYXVzZSB3ZSBhY3QgYXMgaWYgd2UgaGF2ZSBtdWNoIG1vcmUgaW5kZXBlbmRlbnQgb2JzZXJ2YXRpb25zLgoKIyMjIE5vIFR5cGUgSSBlcnJvciBjb250cm9sIQoKYGBge3J9CnNpZ21hV2l0aGluIDwtIHNpZ21hKGxtQmlvcmVwKQpzaWdtYUJldHdlZW4gPC0gc2lnbWEobG1TdW0pCnhCaW9yZXAgPC0gbW9kZWwubWF0cml4KH4gLTEgKyBiaW9yZXAsIGZyYW5jKQp4V3JvbmcgPC0gbW9kZWwubWF0cml4KH5nZW5vdHlwZSwgZnJhbmMpCgoKc2V0LnNlZWQoMjUyMykKblNpbSA8LSAxMDAwCnJlc1dyb25nIDwtIG1hdHJpeChOQSwgblNpbSwgNCkgJT4lIGFzLmRhdGEuZnJhbWUoKQpuYW1lcyhyZXNXcm9uZykgPC0gYygiRXN0aW1hdGUiLCAiU3RkLiBFcnJvciIsICJ0IHZhbHVlIiwgInB2YWx1ZSIpCnJlc0NvcnJlY3QgPC0gcmVzV3JvbmcKZ2Vub3R5cGUgPC0gZnJhbmMkZ2Vub3R5cGUKZ2Vub3R5cGVTdW0gPC0gZnJhbmNTdW0kZ2Vub3R5cGUKYmlvcmVwIDwtIGZyYW5jJGJpb3JlcAoKZm9yIChpIGluIDE6blNpbSkKewogIGJpb3JlcFNpbSA8LSBybm9ybShuY29sKHhCaW9yZXApLCBzZCA9IHNpZ21hQmV0d2VlbikKICB5U2ltIDwtIHhCaW9yZXAgJSolIGJpb3JlcFNpbSArIHJub3JtKG5yb3coeEJpb3JlcCksIHNkID0gc2lnbWFXaXRoaW4pCiAgeVN1bSA8LSBsbSh5U2ltIH4gYmlvcmVwKSRjb2VmZmljaWVudAogIHJlc1dyb25nW2ksIF0gPC0gc3VtbWFyeShsbSh5U2ltIH4gZ2Vub3R5cGUpKSRjb2VmZmljaWVudFsyLCBdCiAgcmVzQ29ycmVjdFtpLCBdIDwtIHN1bW1hcnkobG0oeVN1bSB+IGdlbm90eXBlU3VtKSkkY29lZmZpY2llbnRbMiwgXQp9Cm1lYW4ocmVzQ29ycmVjdCRwdmFsdWUgPCAwLjA1KQptZWFuKHJlc1dyb25nJHB2YWx1ZSA8IDAuMDUpCmBgYAoKYGBge3J9CnFwbG90KHJlc0NvcnJlY3QkcHZhbHVlLCBnZW9tID0gImhpc3RvZ3JhbSIsIGJvdW5kYXJ5ID0gYygwLCAxKSkgKwogIHN0YXRfYmluKGJyZWFrcyA9IHNlcSgwLCAxLCAuMSkpICsKICB4bGFiKCJwdmFsdWUiKSArCiAgZ2d0aXRsZSgiQ29ycmVjdCBhbmFseXNpcyIpCgpxcGxvdChyZXNXcm9uZyRwdmFsdWUsIGdlb20gPSAiaGlzdG9ncmFtIiwgYm91bmRhcnkgPSBjKDAsIDEpKSArCiAgc3RhdF9iaW4oYnJlYWtzID0gc2VxKDAsIDEsIC4xKSkgKwogIHhsYWIoInB2YWx1ZSIpICsKICBnZ3RpdGxlKCJXcm9uZyBhbmFseXNpcyIpCmBgYAoKLSBTbyB3ZSBvYnNlcnZlIHRoYXQgdGhlIGFuYWx5c2lzIHRoYXQgZG9lcyBub3QgYWNjb3VudCBmb3IgcHNldWRvLXJlcGxpY2F0aW9uIGlzIHRvbyBsaWJlcmFsIQoKLSBUaGUgYW5hbHlzaXMgdGhhdCBmaXJzdCBzdW1tYXJpemVzIG92ZXIgdGhlIHRlY2huaWNhbCByZXBlYXRzIGxlYWRzIHRvIGNvcnJlY3QgcC12YWx1ZXMgYW5kIGNvcnJlY3QgdHlwZSBJIGVycm9yIGNvbnRyb2whCgotIFdoYXQgdG8gZG8gd2hlbiB5b3UgaGF2ZSBhbiB1bmVxdWFsIG51bWJlciBvZiB0ZWNobmljYWwgcmVwZWF0czogbW9yZSBhZHZhbmNlZCBtZXRob2RzIGFyZSByZXF1aXJlZAoKICAtIGUuZy4gbWl4ZWQgbW9kZWxzCiAgLSBUaGUgbWl4ZWQgbW9kZWwgZnJhbWV3b3JrIGNhbiBtb2RlbCB0aGUgY29ycmVsYXRpb24gc3RydWN0dXJlIGluIHRoZSBkYXRhCgotIE1peGVkIG1vZGVscyBjYW4gYWxzbyBiZSB1c2VkIHdoZW4gaW5mZXJlbmNlIGJldHdlZW4gYW5kIHdpdGhpbiBibG9ja3MgaXMgbmVlZGVkLCBlLmcuIHNwbGl0LXBsb3QgZGVzaWducy4KCi0gQnV0LCBtaXhlZCBtb2RlbHMgYXJlIGJleW9uZCB0aGUgc2NvcGUgb2YgdGhlIGxlY3R1cmUgc2VyaWVzLgoKIyBOYXR1cmUgbWV0aG9kczogU3BsaXQtcGxvdCBkZXNpZ25zCgpbTmF0dXJlIE1ldGhvZHMgLSBQb2ludCBvZiBTaWduaWZpY2FuY2UgLSBTcGxpdC1wbG90IERlc2lnbnNdKGh0dHBzOi8vd3d3Lm5hdHVyZS5jb20vYXJ0aWNsZXMvbm1ldGguMzI5My5wZGYpCg==
This work is licensed under the CC BY-NC-SA 4.0 licence.