9. Non-parametric statistics - Kruskal Wallis
Lieven Clement
statOmics, Ghent University (https://statomics.github.io)
1 Comparison of \(g\) groups
- Extend \(F\)-test from a one-way ANOVA to non-parametric alternatives.
2 DMH example
Assess genotoxicity of 1,2-dimethylhydrazine dihydrochloride (DMH) (EU directive)
- 24 rats
- four groups with daily DMH dose
- control
- low
- medium
- high
- Genotoxicity in liver using comet assay on 150 liver cells per rat.
- Are there differences in DNA damage due to DMH dose?
2.1 Comet Assay:
- Visualise DNA strand breaks
- Length comet tail is a proxy for strand breaks.

dna <- read_delim("https://raw.githubusercontent.com/GTPB/PSLS20/master/data/dna.txt", delim = " ")
dna$dose <- as.factor(dna$dose)
dnadna %>%
ggplot(aes(x = dose, y = length, fill = dose)) +
geom_boxplot() +
geom_point(position = "jitter")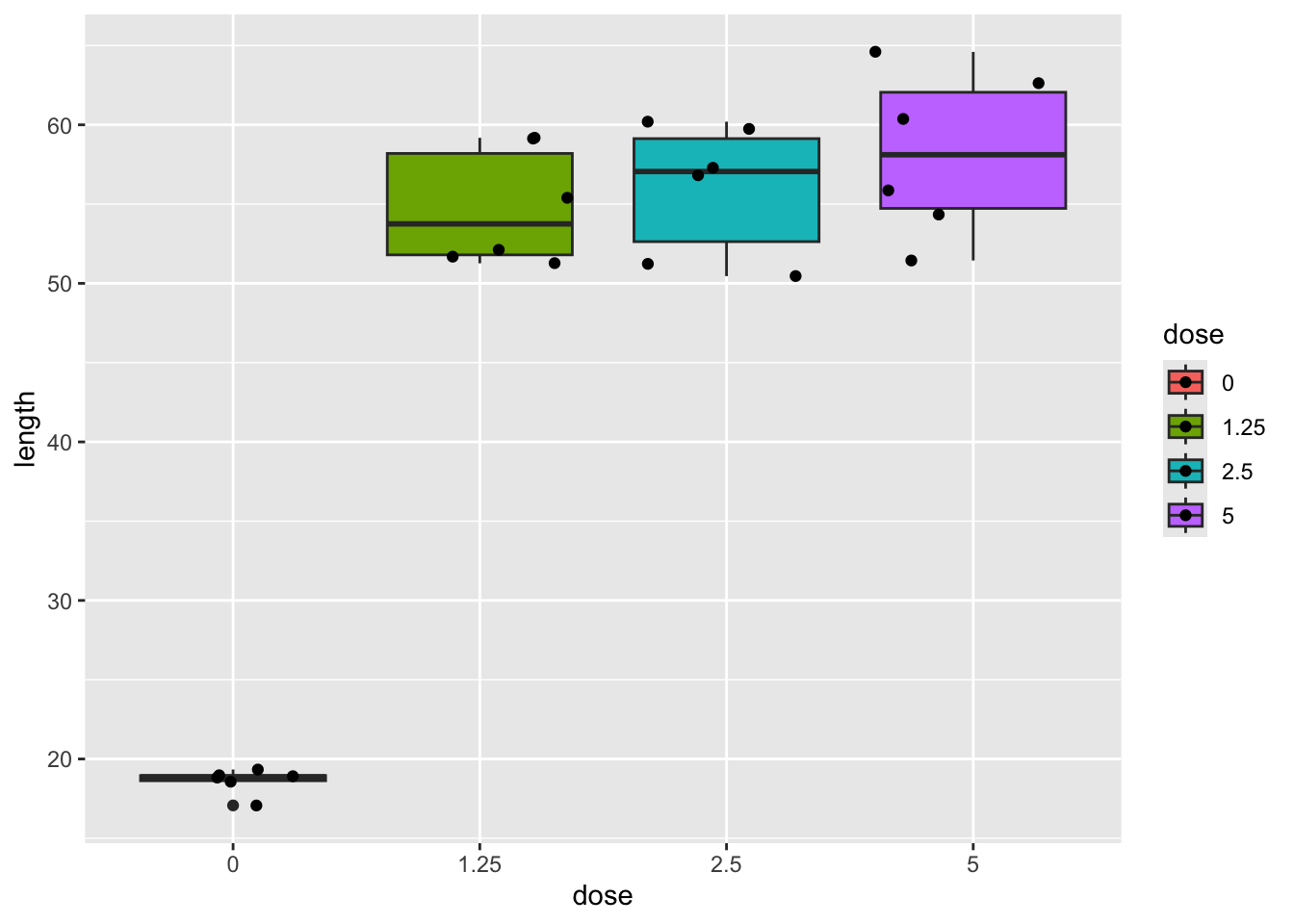
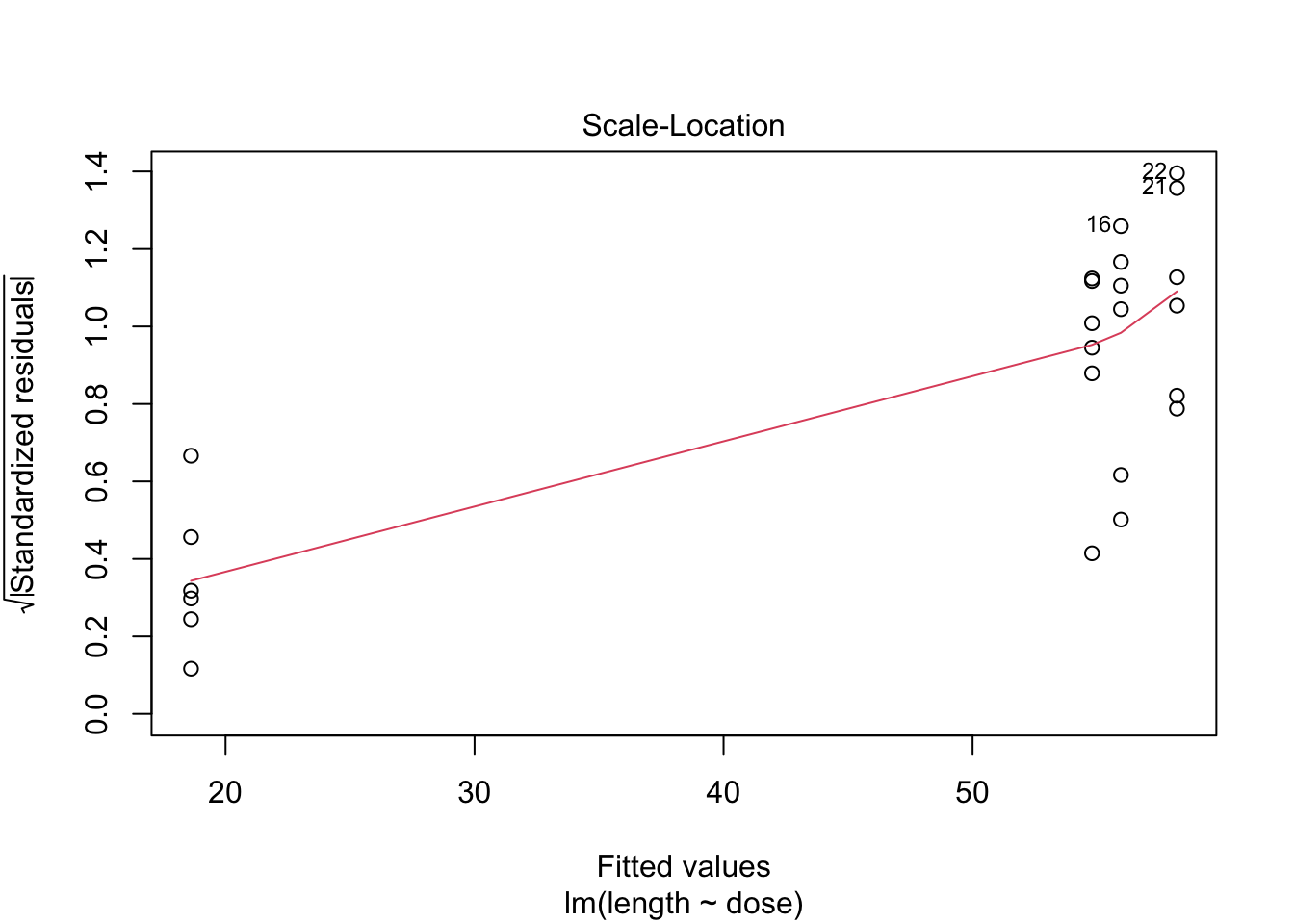
- Strong indication that data in control group has a lower variance.
- 6 observations per group are too few to check the assumptions
3 Kruskal-Wallis Rank Test
The Kruskal-Wallis Rank Test (KW-test) is a non-parameteric alternative for ANOVA F-test.
Classical \(F\)-teststatistic can be written as \[ F = \frac{\text{SST}/(g-1)}{\text{SSE}/(n-g)} = \frac{\text{SST}/(g-1)}{(\text{SSTot}-\text{SST})/(n-g)} , \]
with \(g\) the number of groups.
SSTot depends only on outcomes \(\mathbf{y}\) and will not vary in permutation test.
SST can be used as statistic \[\text{SST}=\sum_{j=1}^t n_j(\bar{Y}_j-\bar{Y})^2\]
The KW test statistic is based on SST on rank-transformed outcomes1, \[ \text{SST} = \sum_{j=1}^g n_j \left(\bar{R}_j - \bar{R}\right)^2 = \sum_{j=1}^t n_j \left(\bar{R}_j - \frac{n+1}{2}\right)^2 , \]
with \(\bar{R}_j\) the mean of the ranks in group \(j\), and \(\bar{R}\) the mean of all ranks, \[ \bar{R} = \frac{1}{n}(1+2+\cdots + n) = \frac{1}{n}\frac{1}{2}n(n+1) = \frac{n+1}{2}. \]
The KW teststatistic is given by \[ KW = \frac{12}{n(n+1)} \sum_{j=1}^g n_j \left(\bar{R}_j - \frac{n+1}{2}\right)^2. \]
The factor \(\frac{12}{n(n+1)}\) is used so that \(KW\) has a simple asymptotic null distribution. In particular under \(H_0\), given thart \(\min(n_1,\ldots, n_g)\rightarrow \infty\), \[ KW \rightarrow \chi^2_{t-1}. \]
The exact KW-test can be executed by calculating the permutation null distribution (that only depends on \(n_1, \ldots, n_g\)) to test \[H_0: f_1=\ldots=f_g \text{ vs } H_1: \text{ at least two means are different}.\]
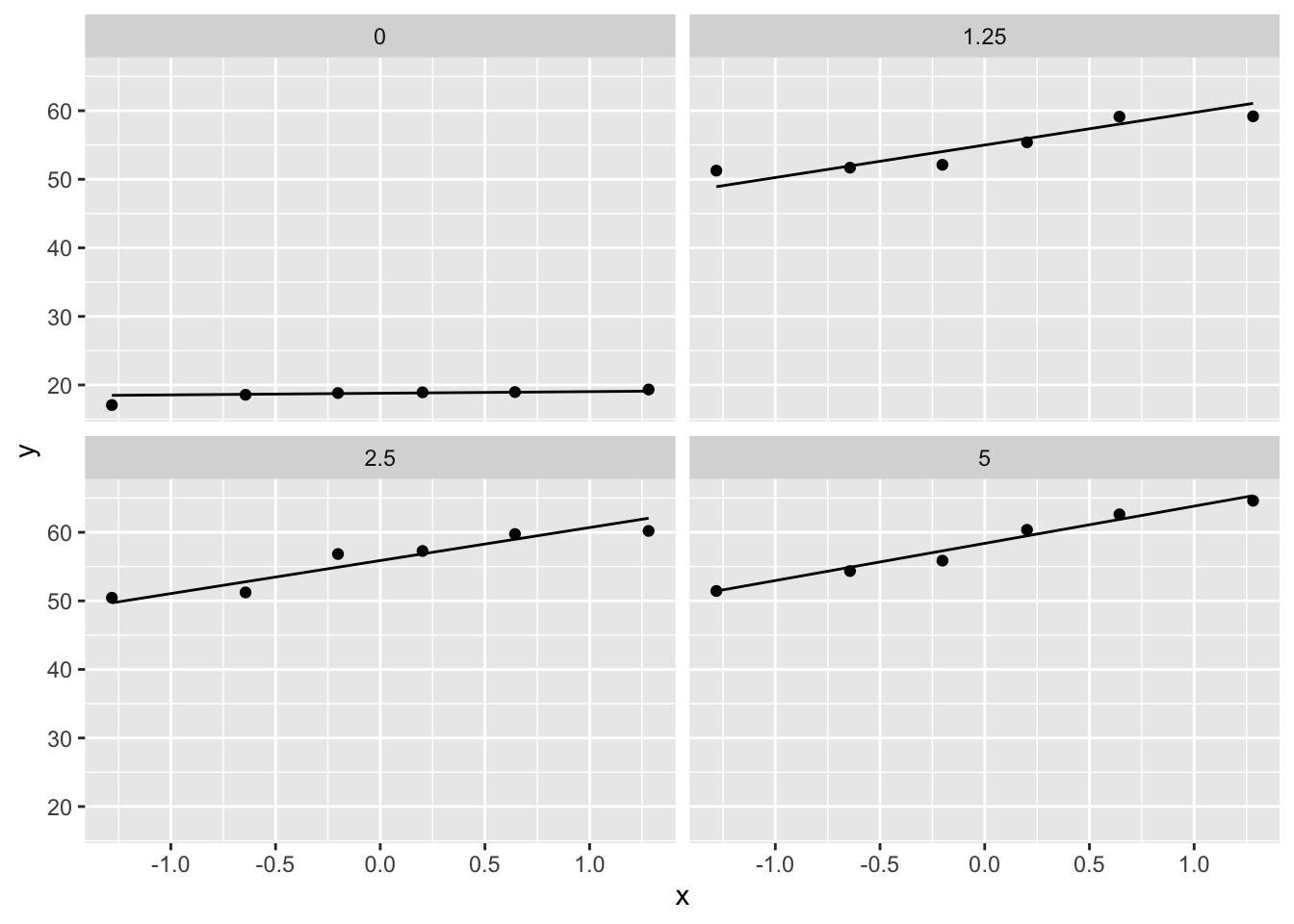
In order to allow \(H_1\) to be formulated in terms of means, the assumption of locations shift should be valid.
For DMH example this is not the case.
If location-shift is invalid, we have to formulate \(H_1\) in terms of probabilistic indices: \[H_0: f_1=\ldots=f_g \text{ vs } H_1: \exists\ j,k \in \{1,\ldots,g\} : \text{P}\left[Y_j\geq Y_k\right]\neq 0.5\]
3.1 DNA Damage Example
Kruskal-Wallis rank sum test
data: length by dose
Kruskal-Wallis chi-squared = 14, df = 3, p-value = 0.002905On the \(5\%\) level of significance we can reject the null hypothesis.
R-functie
kruskal.testonly returns the asymptotic approximation for \(p\)-values.With only 6 observaties per groep, this is not a good approximation of the \(p\)-value
With the
coinR package we can calculate the exacte \(p\)-value
library(coin)
kwPerm <- kruskal_test(length ~ dose,
data = dna,
distribution = approximate(B = 100000)
)
kwPerm
Approximative Kruskal-Wallis Test
data: length by dose (0, 1.25, 2.5, 5)
chi-squared = 14, p-value = 0.00043We conclude that the difference in the distribution of the DNA damages due to the DMH dose is extremely significantly different.
Posthoc analysis with WMW tests.
Pairwise comparisons using Wilcoxon rank sum exact test
data: dna$length and dna$dose
0 1.25 2.5
1.25 0.013 - -
2.5 0.013 0.818 -
5 0.013 0.721 0.788
P value adjustment method: holm - All DMH behandelingen are significantly different from the control.
- The DMH are not significantly different from one another.
- U1 does not occur in the
pairwise.wilcox.testoutput. Point estimate on probability on higher DNA-damage?
nGroup <- table(dna$dose)
probInd <- combn(levels(dna$dose), 2, function(x) {
test <- wilcox.test(length ~ dose, subset(dna, dose %in% x))
return(test$statistic / prod(nGroup[x]))
})
names(probInd) <- combn(levels(dna$dose), 2, paste, collapse = "vs")
probInd 0vs1.25 0vs2.5 0vs5 1.25vs2.5 1.25vs5 2.5vs5
0.0000000 0.0000000 0.0000000 0.4444444 0.2777778 0.3333333 Because there are doubts on the location-shift model we draw our conclusions in terms of the probabilistic index.
3.1.1 Conclusion
- There is an extremely significant difference in in the distribution of the DNA-damage measurements due to the treatment with DMH (\(p<0.001\) KW-test).
- DNA-damage is more likely upon DMH treatment than in the control treatment (all p=0.013, WMW-testen).
- The probability on higher DNA-damage upon exposure to DMH is 100% (Calculation of a CI on the probabilistic index is beyond the scope of the course)
- There are no significant differences in the distributions of the comit-lengths among the treatment with the different DMH concentrations (\(p=\) 0.72-0.82).
- DMH shows already genotoxic effects at low dose.
- (Alle paarswise tests are gecorrected for multiple testing using Holm’s methode).
we assume that no ties are available↩︎
