Practicum 2: Witte bloedcellen

1 Concentratie witte bloedcellen bij ratten

Test 2023-2024

De data die we hier beschouwen zijn afkomstig van een studie waarbij men een behandelde groep van 16 ratten met de pertussis bacteria heeft geïnfecteerd. Men mat vervolgens de concentratie van de witte bloedcellen (WBC) in aantal per kubieke mm. In een controlegroep van 24 ratten werd eveneens de concentratie van witte bloedcellen gemeten.

De data is beschikbaar in het bestand wbcon.dat. Dit bestand bevat twee variabelen, de variabele WBC die de concentratie witte bloedcellen weergeeft en de variabele groep die twee mogelijke waarden kan aannemen:

• 0: de rat behoort tot de controlegroep
• 1: de rat behoort tot de behandelde groep

library(ggplot2)
library(dplyr)

## 
## Attaching package: 'dplyr'

## The following objects are masked from 'package:stats':
## 
##     filter, lag

## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union

#install.packages("tidyr")
library(tidyr)

Lees de dataset wbcon.dat in.

wbcon <- read.table("https://raw.githubusercontent.com/statOmics/statistiekBasisCursusData/master/practicum3/wbcon.dat", header = TRUE)

2 Data-exploratie

2.1 Is de gemiddelde concentratie witte bloedcellen groter in de controlegroep of in de behandelde groep?

wbSum <- wbcon %>%
  group_by(groep) %>%
  summarize_at("WBC", 
               list(mean=~mean(.,na.rm=TRUE),
                    sd=~sd(.,na.rm=TRUE),
                    n=function(x) x%>%is.na%>%`!`%>%sum)
                ) %>%
  mutate(se = sd/sqrt(n))
wbSum

Na pertrussis infectie verdriedubbelt het aantal witte bloedcellen/mm\(^3\). Maar is dit verschil significant?

2.2 Figuur van de ruwe gegevens

wbcon$groep <- as.factor(wbcon$groep) # groep is integer, we willen een factor
boxplot <- ggplot(data=wbcon,aes(x=groep, y=WBC, col=groep)) + 
  geom_boxplot(outlier.shape=NA) + 
  geom_jitter() +
  theme_bw() + 
  ggtitle("Concentratie witte bloedcellen")

boxplot 

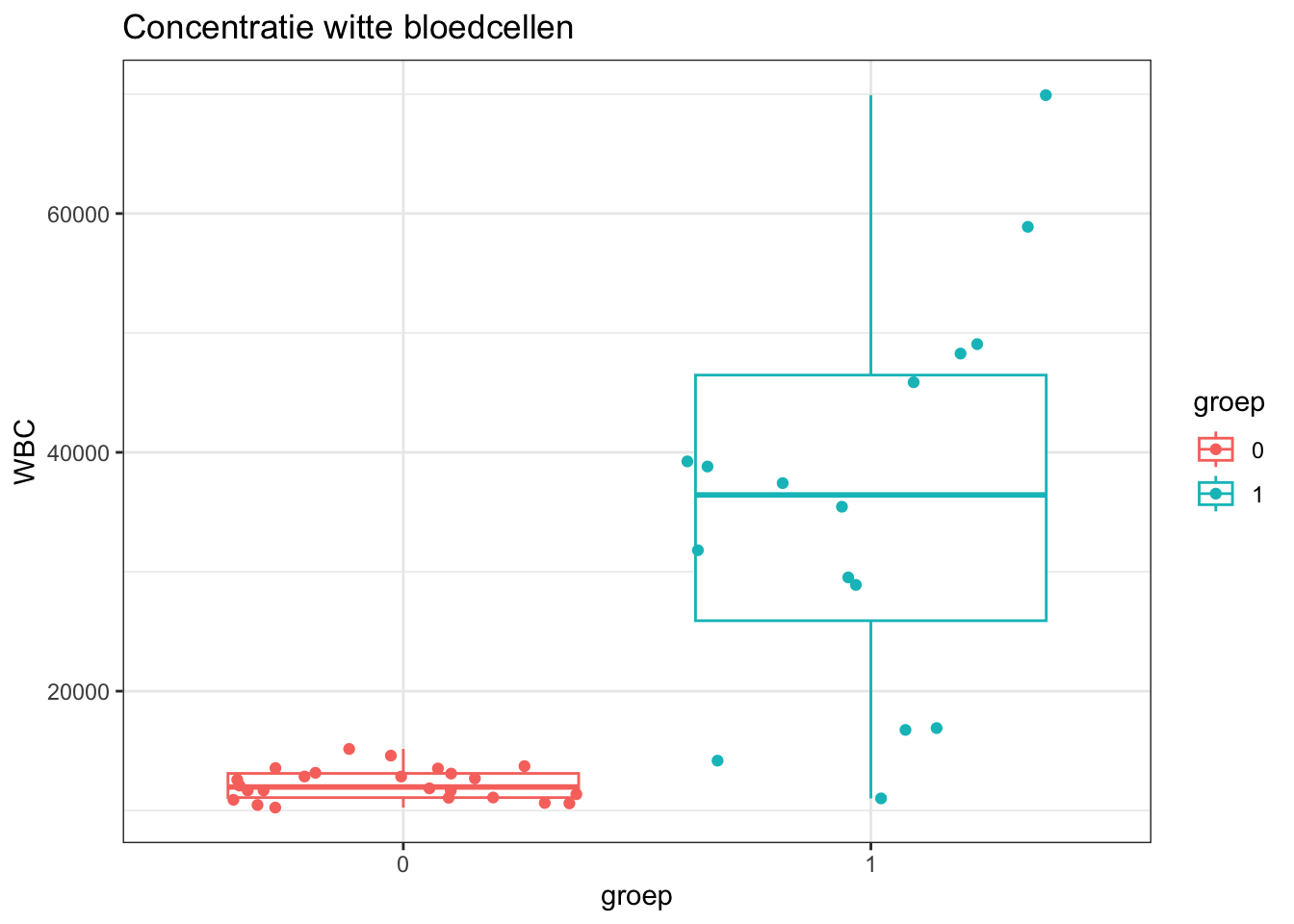
Op de boxplots zien we dat de variantie tussen beide groepen erg verschillend is.

3 Aannames voor de statistische toets

Welke test moeten we uitvoeren om na te gaan of de gemiddelde concentratie witte bloedcellen verschillend is in de controle versus de behandelde groep? Welke voorwaarden moeten we hiervoor nagaan?

Het experiment werd opgezet met 40 ratten. 16 ratten werden at random toegewezen aan de behandelingsgroep en de overige ratten kregen een controle behandeling. Dit betekent dat de data ongepaard zijn en dat we dus een ongepaarde two sample t-test zullen uitvoeren. De voorwaarden voor deze test zijn de volgende:

• onafhankelijke observaties
• concentratie witte bloedcellen in elke groep normaal verdeeld
• gelijkheid van variantie

Onafhankelijkheid kan worden verkregen door studiedesign. We gaan ervan uit dat de ratten die betrokken zijn in de studie onafhankelijk werden getrokken uit de populatie van ratten.

Om na te gaan of de concentratie witte bloedcellen in beide groepen normaal verdeeld zijn, maken we 2 QQ-plots.

qqplot <- wbcon %>% 
  ggplot(aes(sample=WBC)) +
  geom_qq() +
  geom_qq_line() +
  facet_wrap(~groep)
qqplot

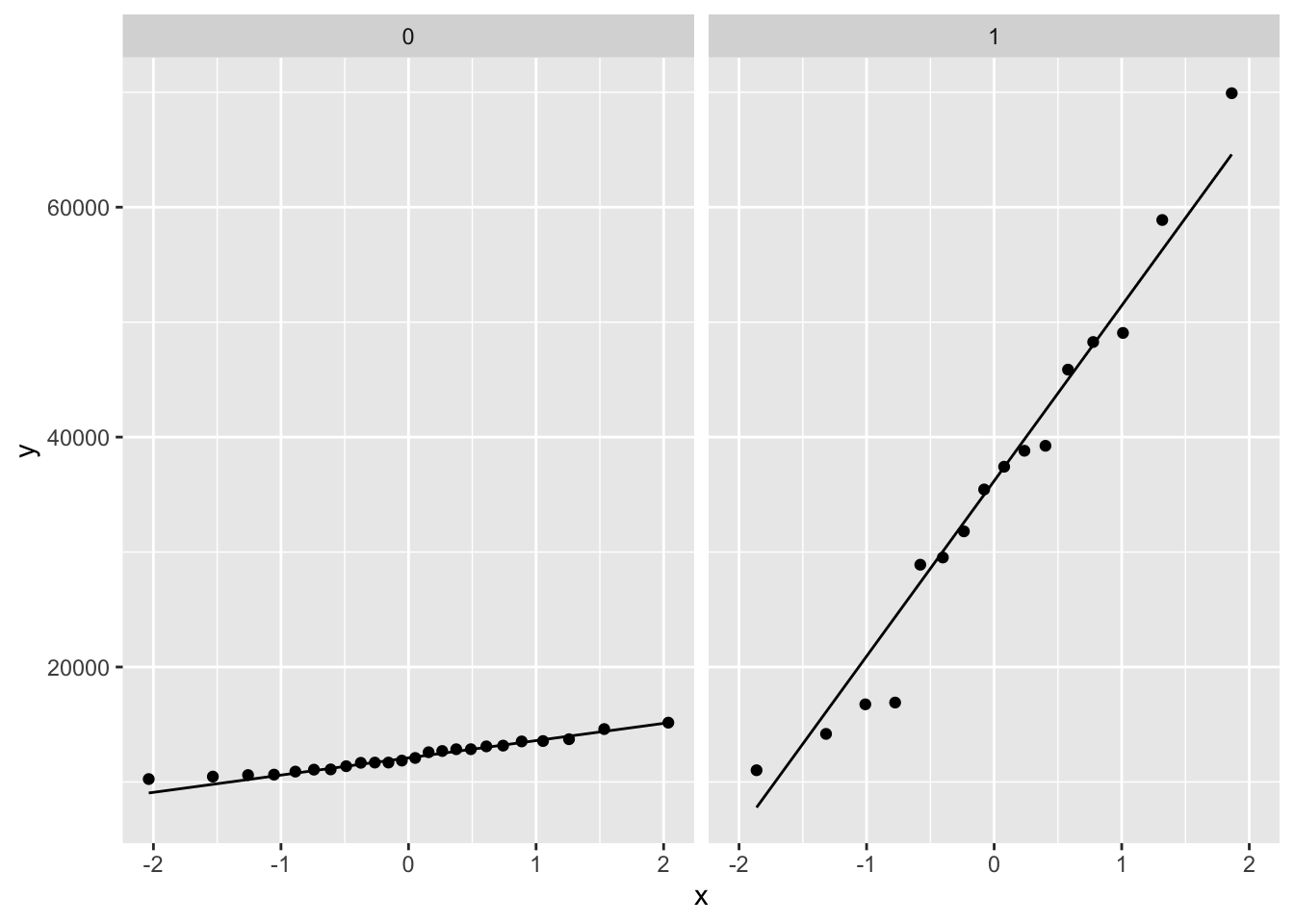
Meer informatie over QQ-plots kan je terugvinden in kennisclip “4.4 De Normale benadering van gegevens” in de statistiekcursus (dodona, html, youtube).

Uit de boxplot bleek dat de variantie van de gegevens niet gelijk was. Daarom kunnen we geen gebruik maken van de gepoolde variantieschatter en voeren we een Welch-modified two sample t-test uit.

4 Hypothesis en statistische toets

Formuleer de nul- en alternatieve hypothese voor een tweezijdige test. Voer deze test uit op het 5% significantieniveau.

4.1 Nul- en alternatieve hypothese

We willen nagaan of de gemiddelde concentratie witte bloedcellen in de controlegroep significant verschilt van de gemiddelde concentratie witte bloedcellen in behandelde groep. De nul- en alternatieve hypothese horende voor het toetsen van deze onderzoeksvraag zijn:

Nulhypothese

• In symbolen: \(H_0: \mu_0 = \mu_1\)
• In woorden: \(H_0:\) de gemiddelde concentratie witte bloedcellen in controlegroep is gelijk aan de gemiddelde concentratie witte bloedcellen in behandelde groep.

Alternatieve hypothese

• In symbolen : \(H_A: \mu_0 \neq \mu_1\)
• In woorden: \(H_A:\) de gemiddelde concentratie witte bloedcellen in controlegroep is verschillend van de gemiddelde concentratie witte bloedcellen in behandelde groep.

met \(\mu_0\): het populatiegemiddelde van de concentratie witte bloedcellen bij ratten na behandeling met de controle en \(\mu_1\): het populatiegemiddelde van de concentratie witte bloedcellen bij ratten na infectie met de pertrussis bacteriën.

4.2 Tweezijdige two sample t-test met ongelijkheid van variantie

Bij de t-test functie is het argument var.equal default var.equal = FALSE zodat de Welch t-test wordt uitgevoerd waarbij wordt gewerkt met een afzonderlijke variantieschatter per groep.

test <- t.test(WBC ~ groep,wbcon)
test

## 
##  Welch Two Sample t-test
## 
## data:  WBC by groep
## t = -5.7114, df = 15.132, p-value = 3.984e-05
## alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
## 95 percent confidence interval:
##  -32311.32 -14758.47
## sample estimates:
## mean in group 0 mean in group 1 
##        12215.92        35750.81

4.3 Interpretatie

De t-test heeft een p-waarde van 4e-05. Deze p-waarde is veel kleiner dan het vooropgestelde significantieniveau \(\alpha=0.05\). Hierdoor kunnen we de nulhypothese kunnen verwerpen op het 5% significantieniveau. Dit betekent dat concentratie witte bloedcellen gemiddeld significant verschillend is tussen ratten die de controle behandeling kregen en ratten die geïnfecteerd werden met pertrussis.

De t-test geeft ook een 95% betrouwbaarheidsinterval weer van -32311 tot -14758.

We hebben dus geschat dat het werkelijke gemiddelde verschil in concentratie witte bloedcellen tussen de controle groep en de behandelde groep met 95% kans tussen -32311 bloedcellen/mm\(^3\) en -14758 ligt.

5 Conclusie

De gemiddelde witte bloedcelconcentratie is extreem significant verschillend tussen ratten die geïnfecteerd worden met pertrussis en ratten die de controle behandeling ondergaan (p << 0.001). De witte bloedcelconcentratie is gemiddeld 23535 bloedcellen/mm\(^3\) hoger bij ratten na infectie met pertrussis dan bij ratten die de controlebehandeling ondergaan (95% BI [14758, 32311]).

---

This work is licensed under the CC BY-NC-SA 4.0 licence.