10. Algemeen Lineair Model - Factoriële Designs

1 Introductie

In deze sectie illustreren we hoe experimenten met een factoriële proefopzet geanalyseerd kunnen worden met het algemeen lineair model.

We focussen hierbij op een two-way anova design waarbij we een continue response modelleren in functie van twee categorische predictor variabelen (factoren).

2 Data

48 ratten werden at random toegewezen aan

• 3 giffen (I,II,III) and
• 4 behandelingen (A,B,C,D),

en,

• de overlevingstijd werd opgemeten (eenheid: 10 h)

We transformeren de data eerst naar uren

library(faraway)
data(rats)

rats <- rats %>% 
  mutate(time=time * 10)

library(GGally)
rats %>% 
  ggpairs()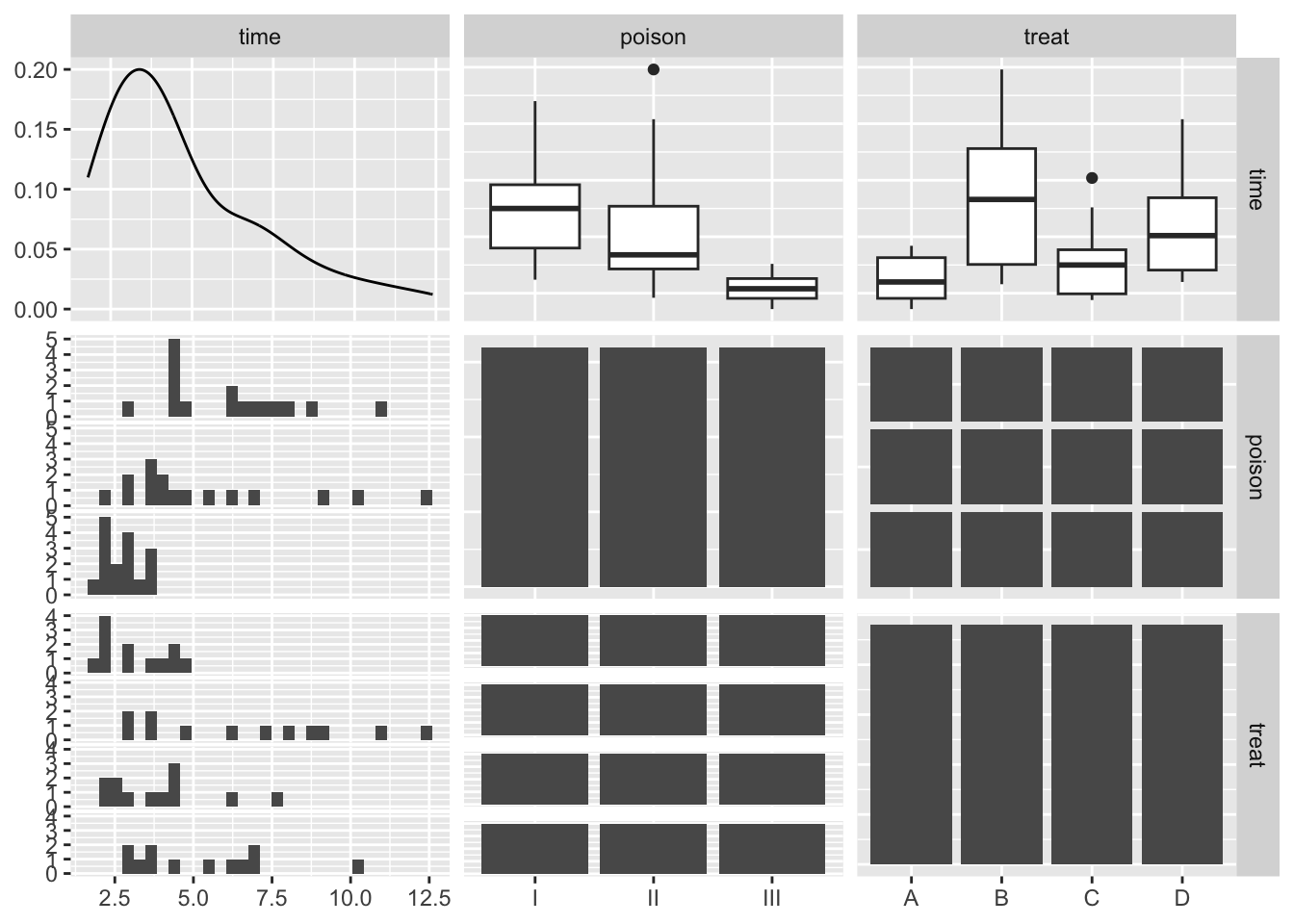

De data exploratie suggereert een effect van beide factoren.

rats %>%
  ggplot(aes(x=treat,y=time)) + 
  geom_boxplot(outlier.shape=NA) + 
  geom_jitter() +
  facet_wrap(~poison) +
  ylab("time (h)")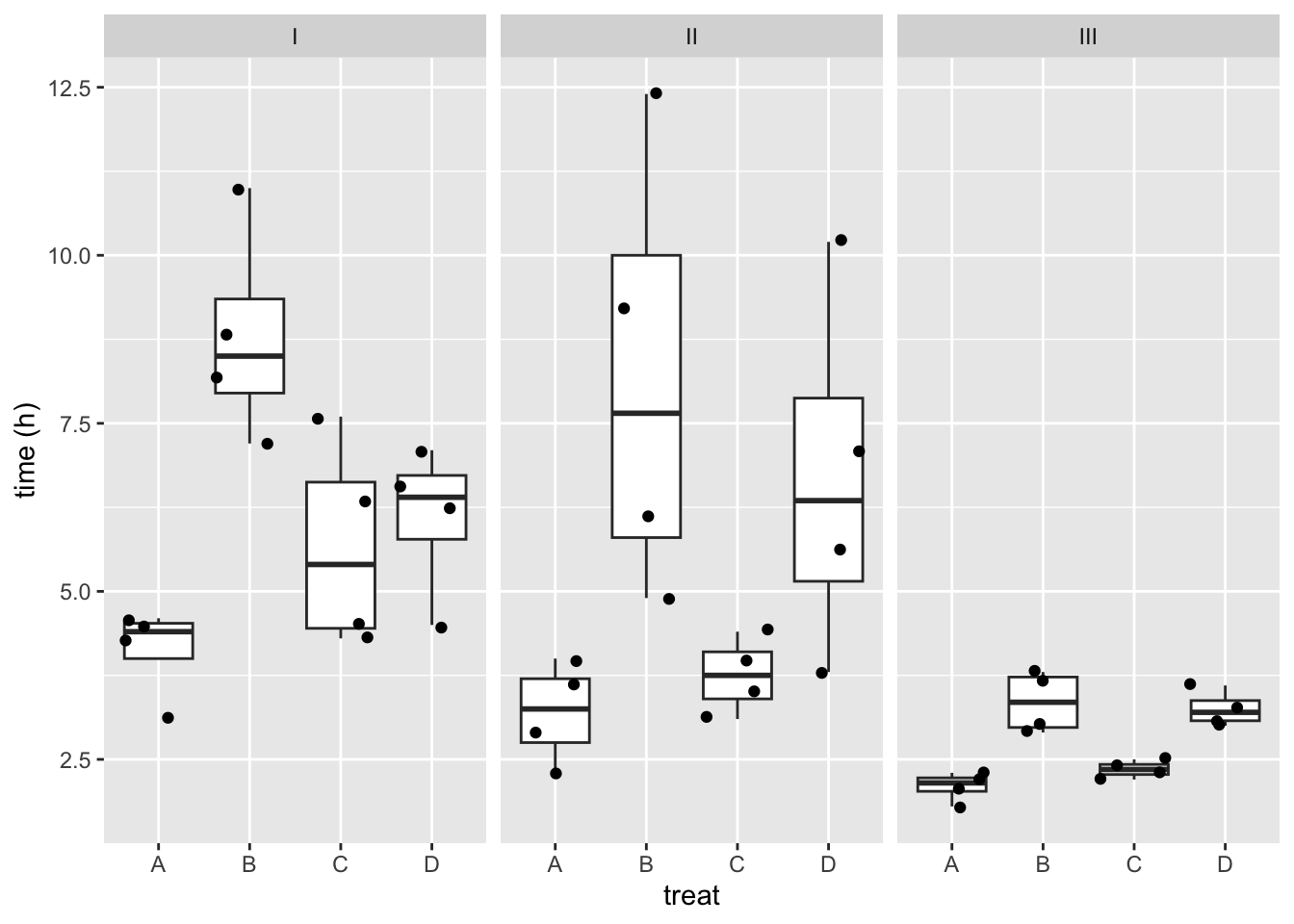

• Er zou een interactie kunnen zijn tussen behandeling en gif, het effect van het gif op de overlevingstijd hangt dan af van de behandeling en vice versa.
• De boxplots geven ook aan dat de data heteroscedastisch zijn.

3 Model

We modelleren de data met een hoofdeffect voor gif en behandeling en een gif \(\times\) behandeling interactie.

\[ \begin{array}{lcl} y_i &=& \beta_0 + \\ &&\beta_{II} x_{iII} + \beta_{III} x_{iIII} + \\ && \beta_{B} x_{iB} + \beta_{C} x_{iC} + \beta_{D} x_{iD} + \\ &&\beta_{II:B}x_{iII}x_{iB} + \beta_{II:C}x_{iII}x_{iC} + \beta_{II:D}x_{iII}x_{iD} + \\ &&\beta_{III:B}x_{iIII}x_{iB} + \beta_{III:C}x_{iIII}x_{iC} + \beta_{III:D}x_{iIII}x_{iD} + \epsilon_i \end{array} \]

met \(i = 1, \ldots, n\), \(n=48\), en, \(x_{iII}\), \(x_{iIII}\), \(x_{iB}\), \(x_{iC}\) en \(x_{iD}\) dummy variabelen voor respectievelijk gif II, III, behandeling B, C, en D.

rats1 <- lm(time~poison*treat, rats)
summary(rats1)

Call:
lm(formula = time ~ poison * treat, data = rats)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.2500 -0.4875  0.0500  0.4312  4.2500 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)        4.1250     0.7457   5.532 2.94e-06 ***
poisonII          -0.9250     1.0546  -0.877   0.3862    
poisonIII         -2.0250     1.0546  -1.920   0.0628 .  
treatB             4.6750     1.0546   4.433 8.37e-05 ***
treatC             1.5500     1.0546   1.470   0.1503    
treatD             1.9750     1.0546   1.873   0.0692 .  
poisonII:treatB    0.2750     1.4914   0.184   0.8547    
poisonIII:treatB  -3.4250     1.4914  -2.297   0.0276 *  
poisonII:treatC   -1.0000     1.4914  -0.671   0.5068    
poisonIII:treatC  -1.3000     1.4914  -0.872   0.3892    
poisonII:treatD    1.5000     1.4914   1.006   0.3212    
poisonIII:treatD  -0.8250     1.4914  -0.553   0.5836    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.491 on 36 degrees of freedom
Multiple R-squared:  0.7335,    Adjusted R-squared:  0.6521 
F-statistic:  9.01 on 11 and 36 DF,  p-value: 1.986e-07

plot(rats1)

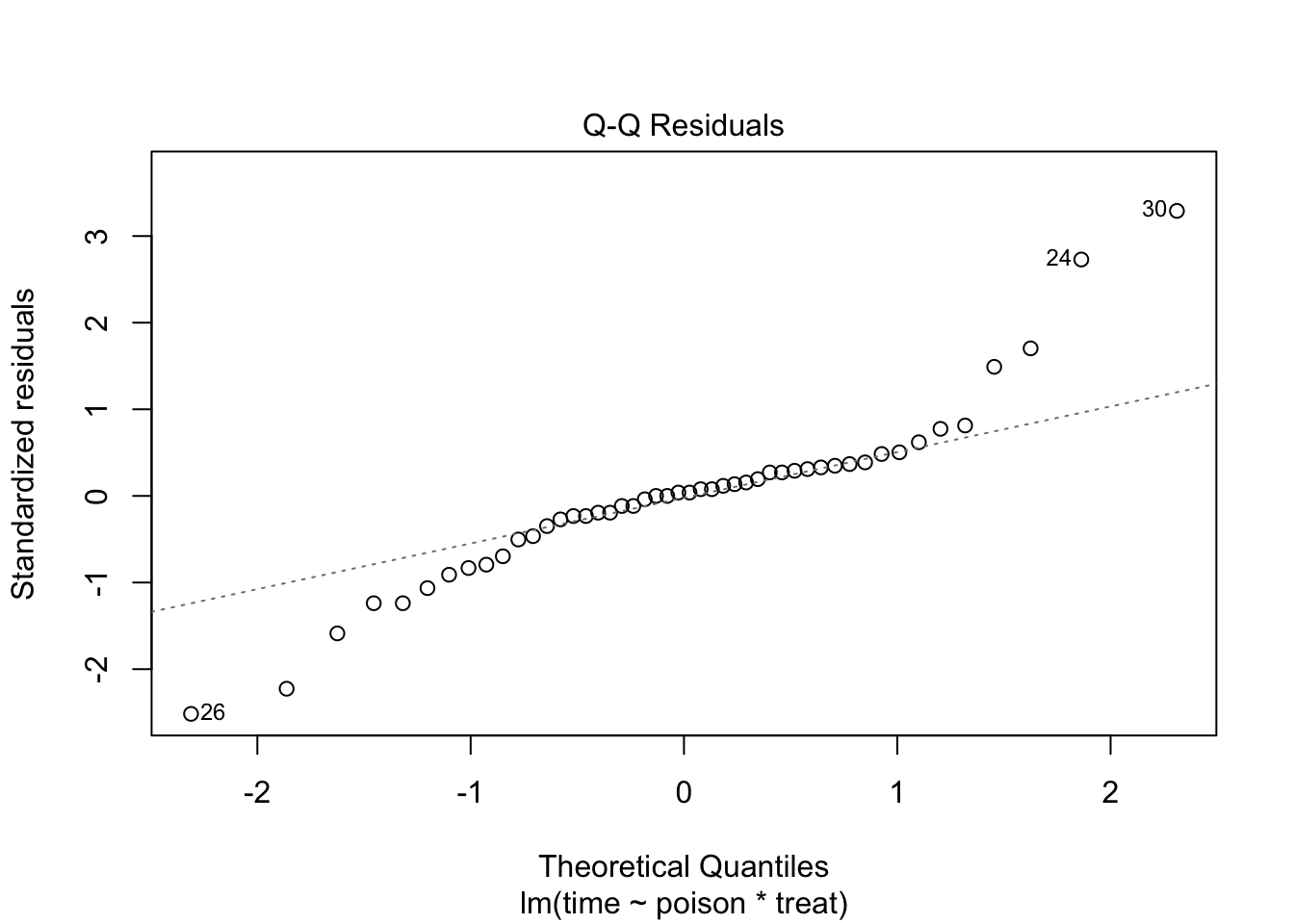
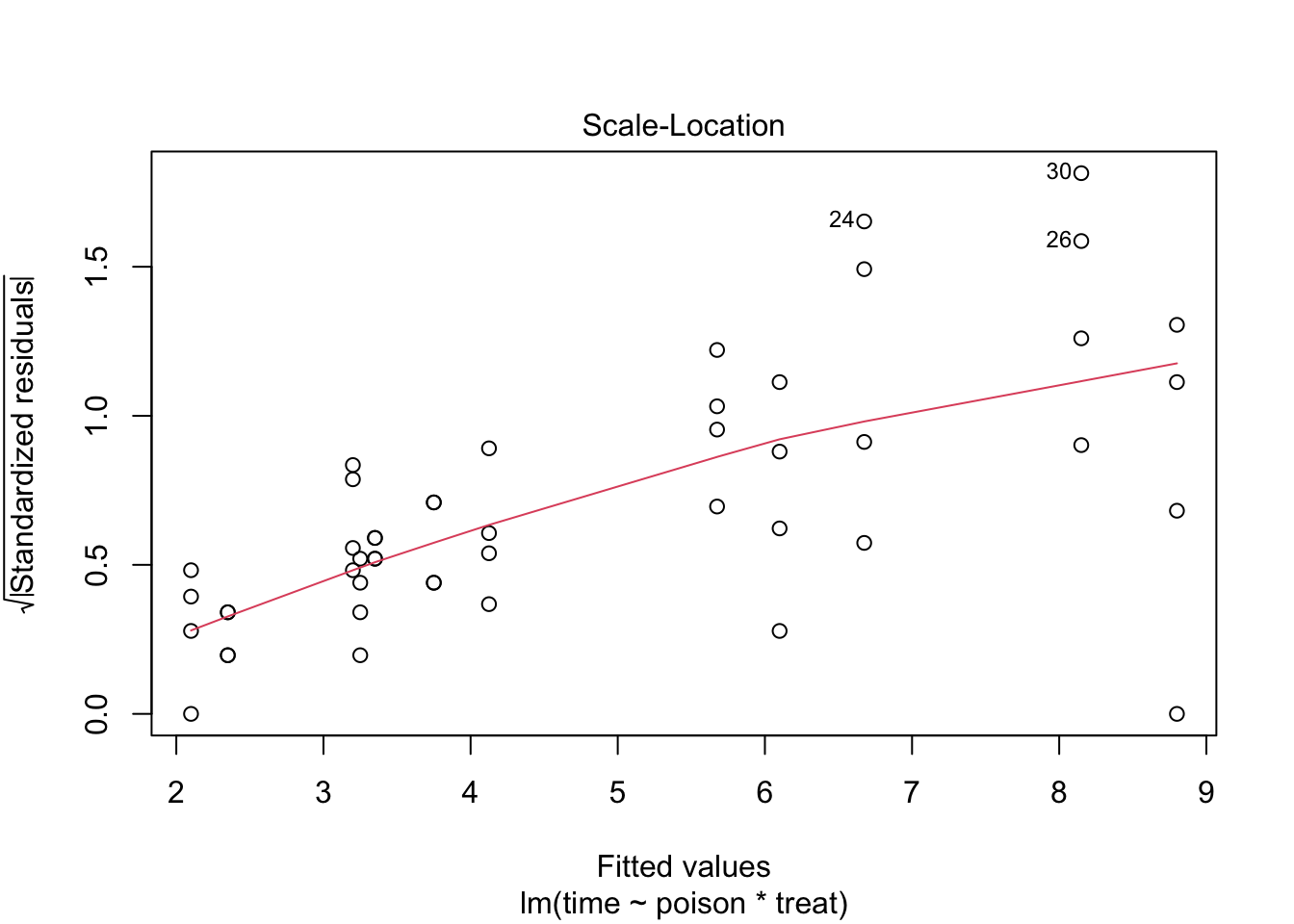
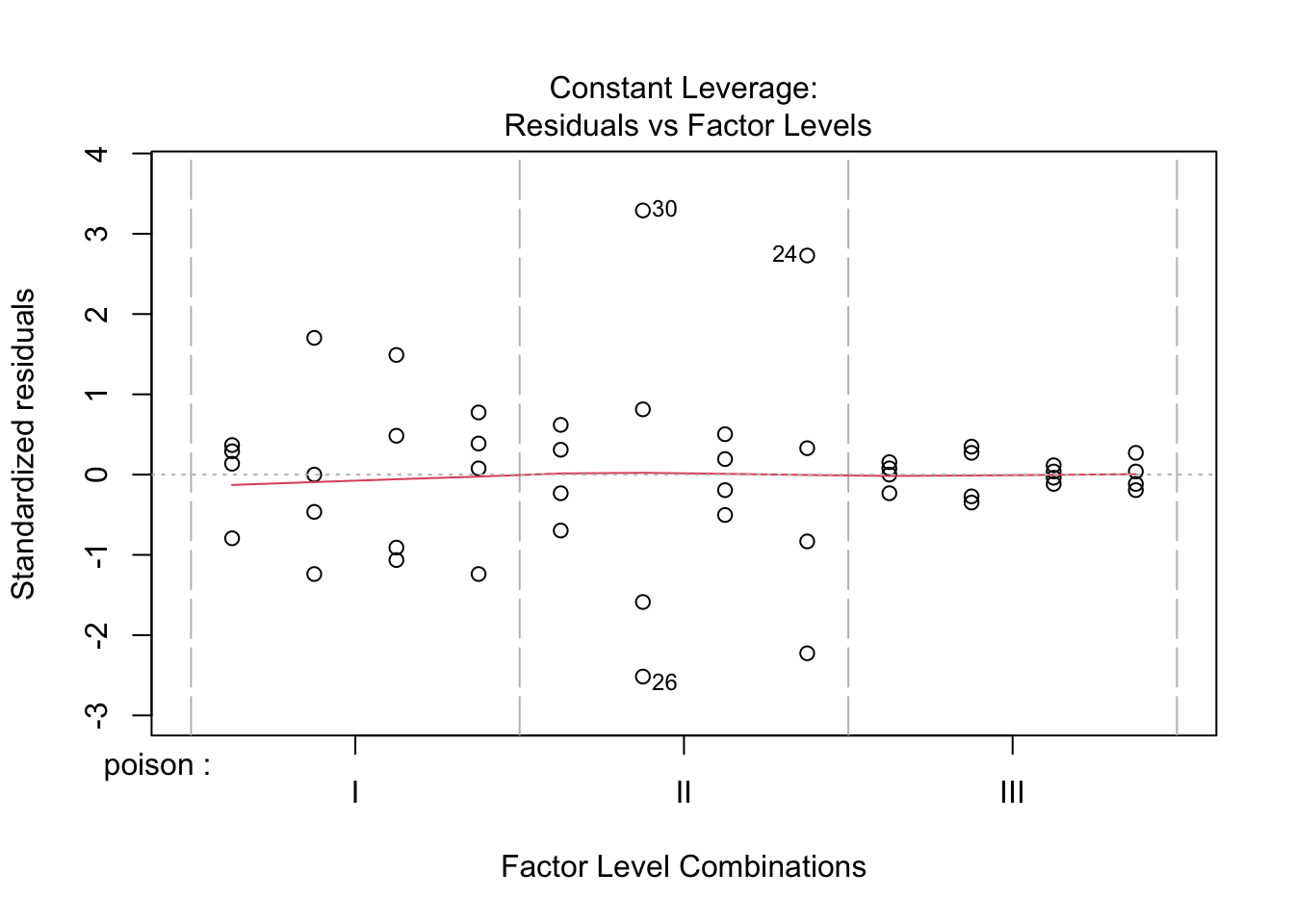
De errors zijn heteroscedastisch. De residu plot suggereert een relatie tussen gemiddelde en variantie. De QQ-plot suggereert dat de verdeling mogelijks bredere staarten heeft dan de normale verdeling.

3.1 Transformaties

3.1.1 Logaritmische transformatie

rats %>%
  ggplot(aes(x=treat,y=log2(time))) + 
  geom_boxplot(outlier.shape=NA) + 
  geom_jitter() +
  facet_wrap(~poison)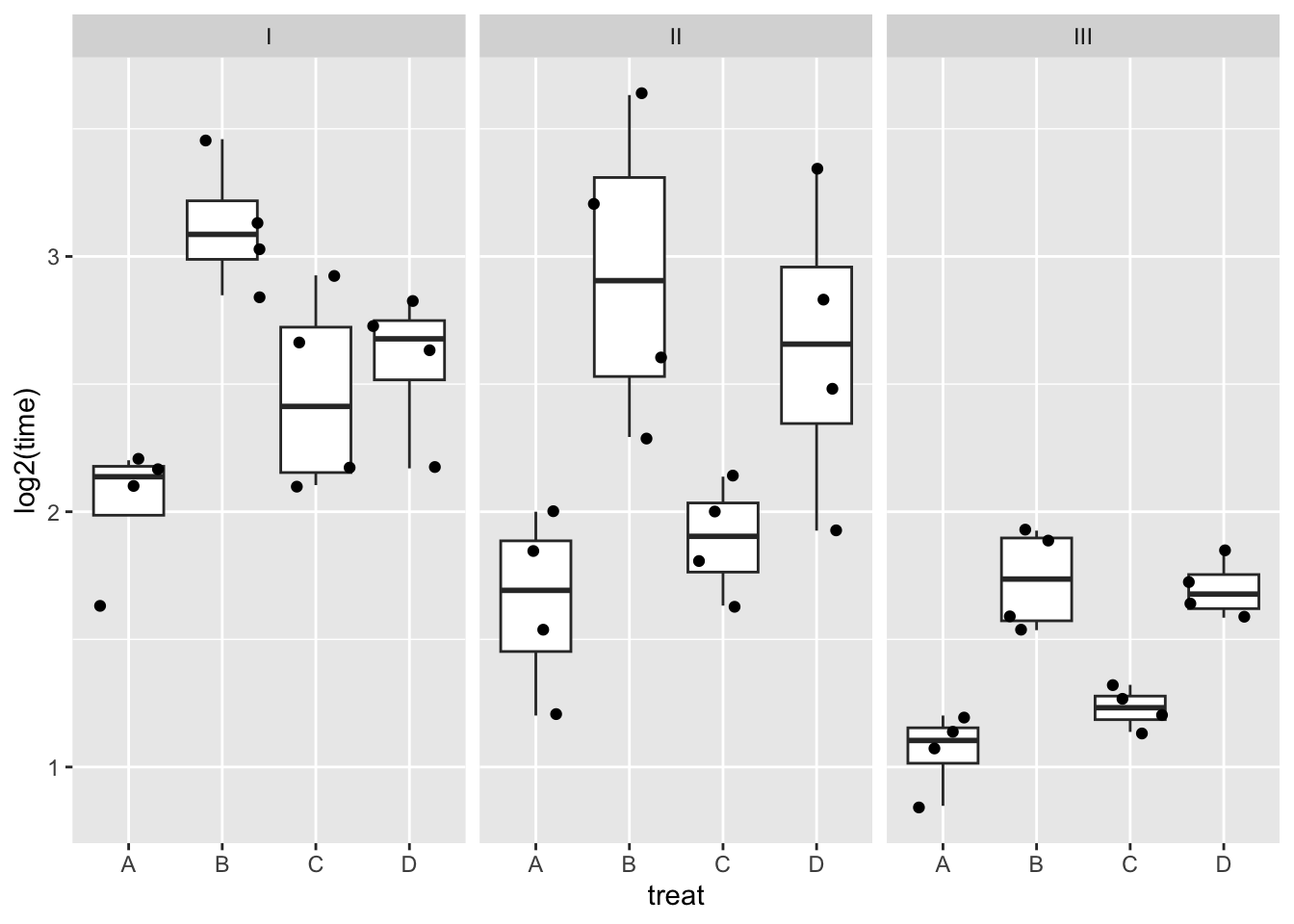

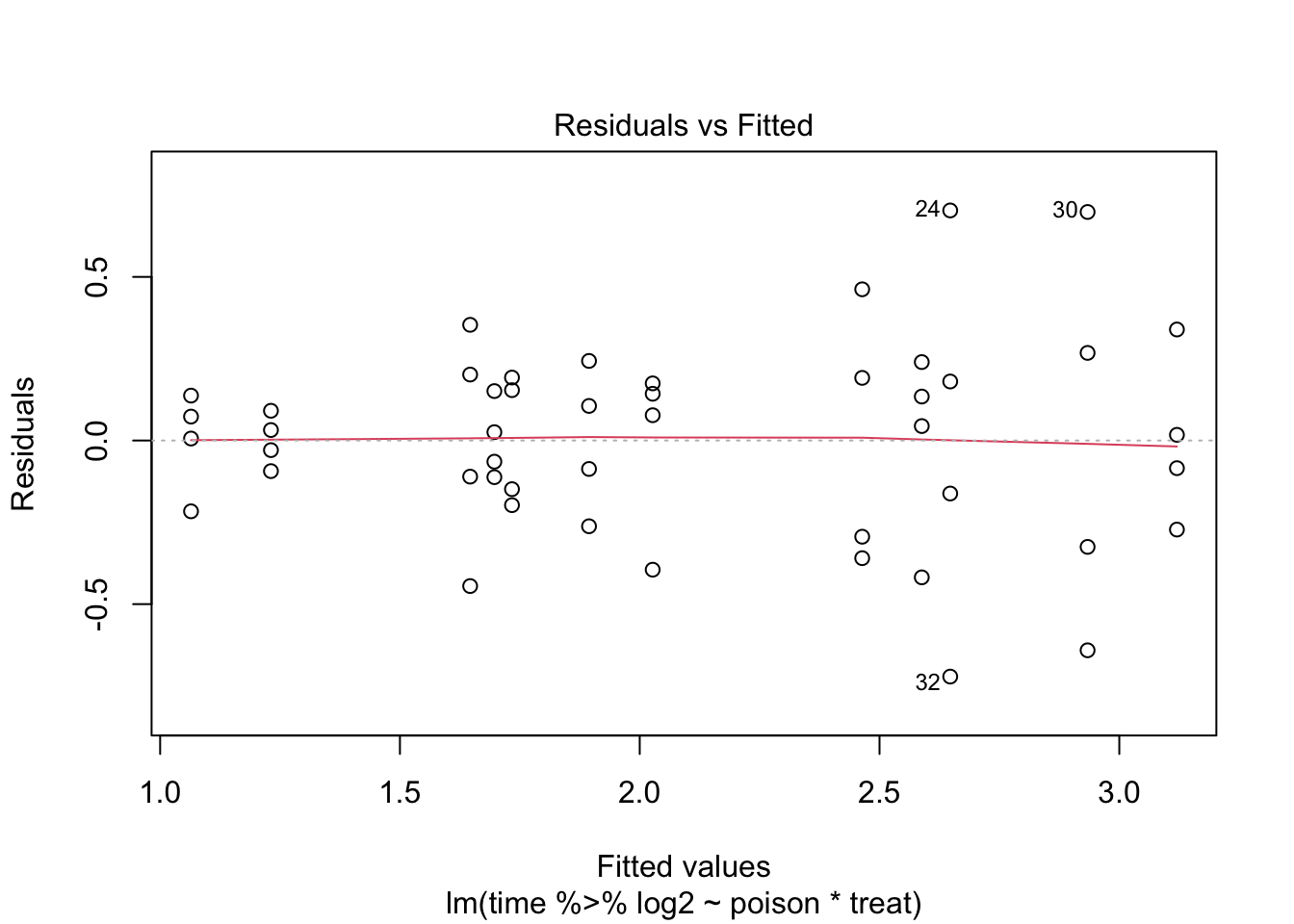
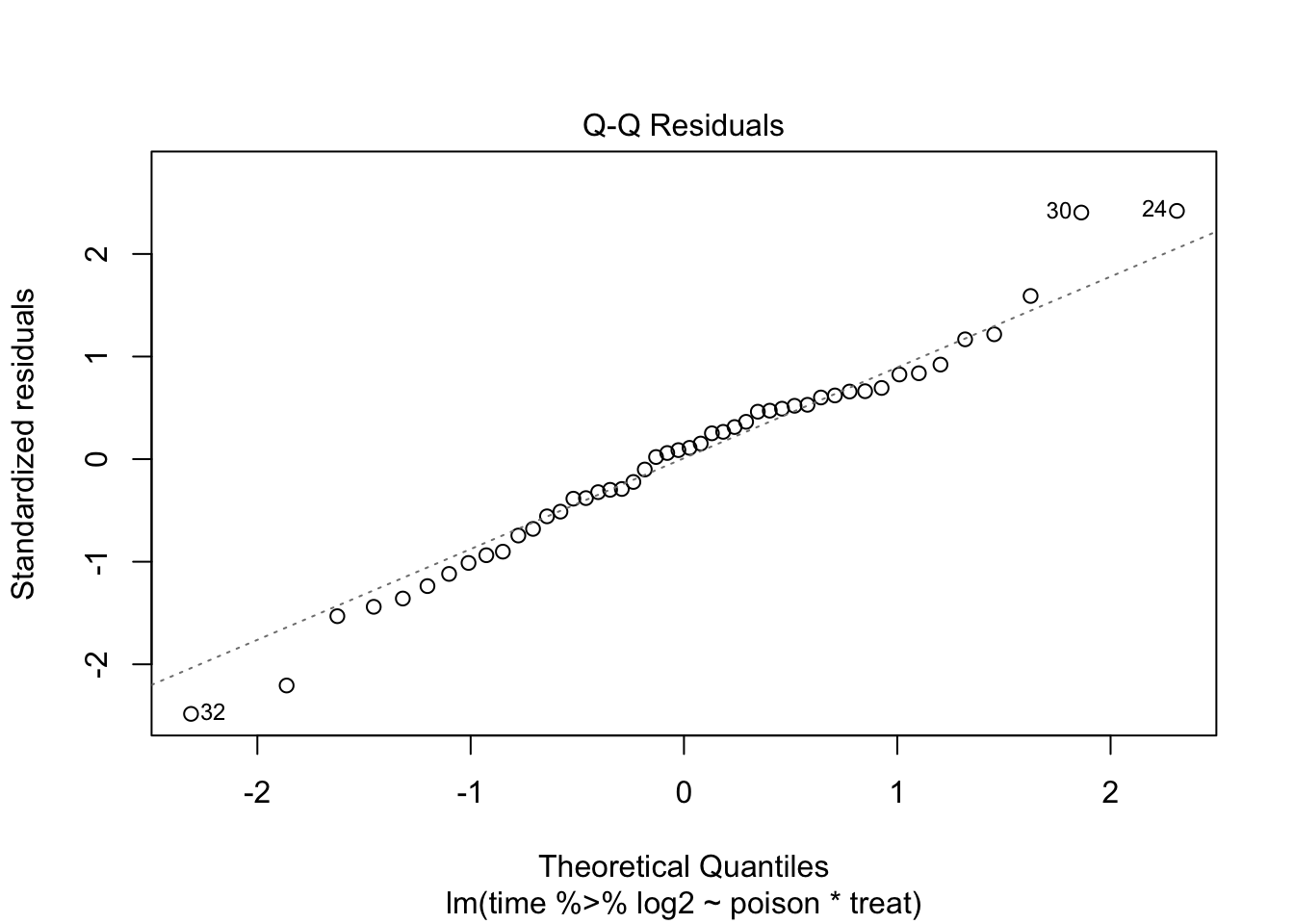
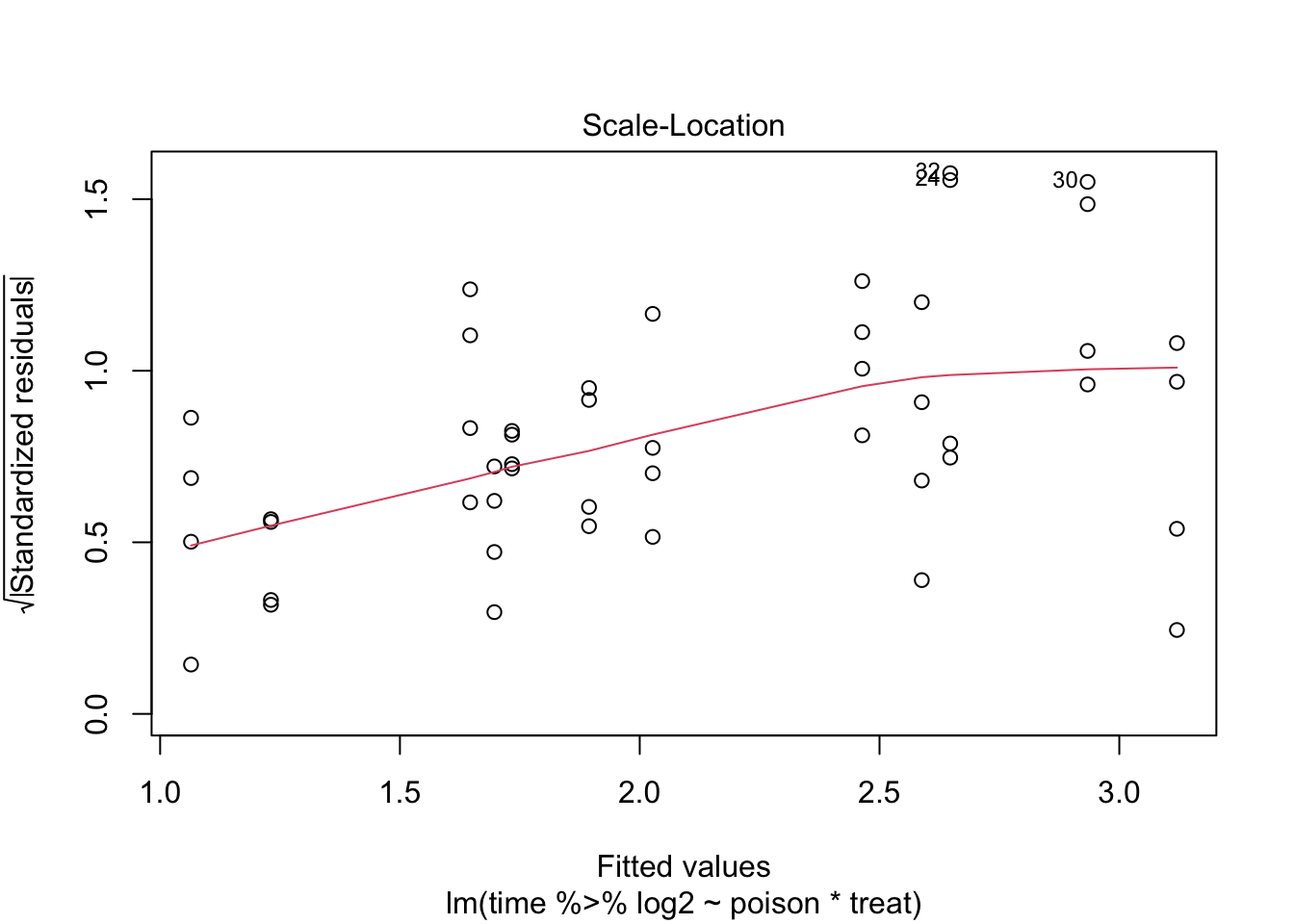
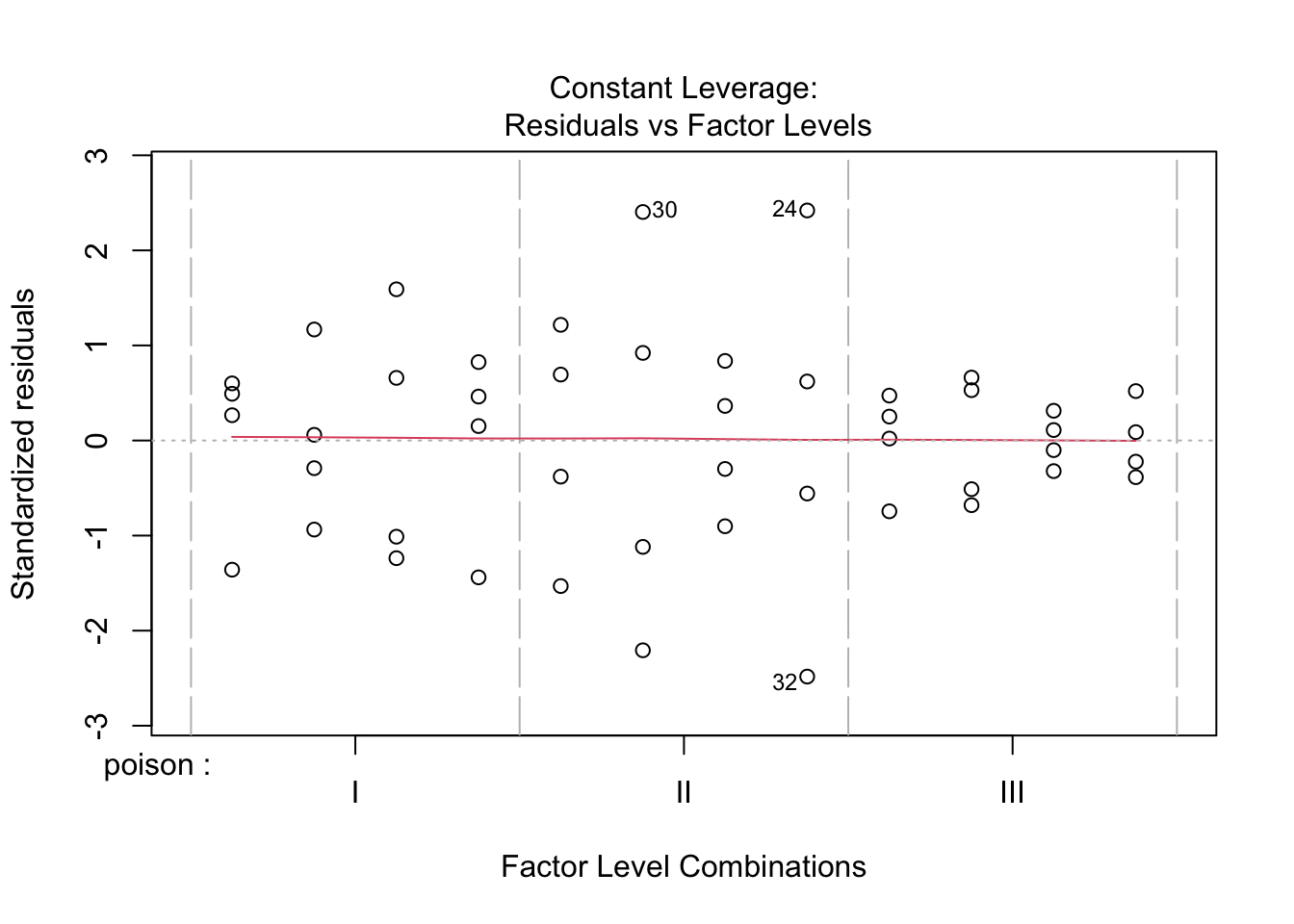
rats2 <- lm(time %>% log2~poison*treat, rats)
plot(rats2)

Log transformatie verwijdert heteroscedasticiteit niet volledig.

3.1.2 Reciproke transformatie

rats %>%
  ggplot(aes(x=treat,y=1/time)) + 
  geom_boxplot(outlier.shape=NA) + 
  geom_jitter() +
  facet_wrap(~poison) + 
  ylab ("rate of dying (1/h)")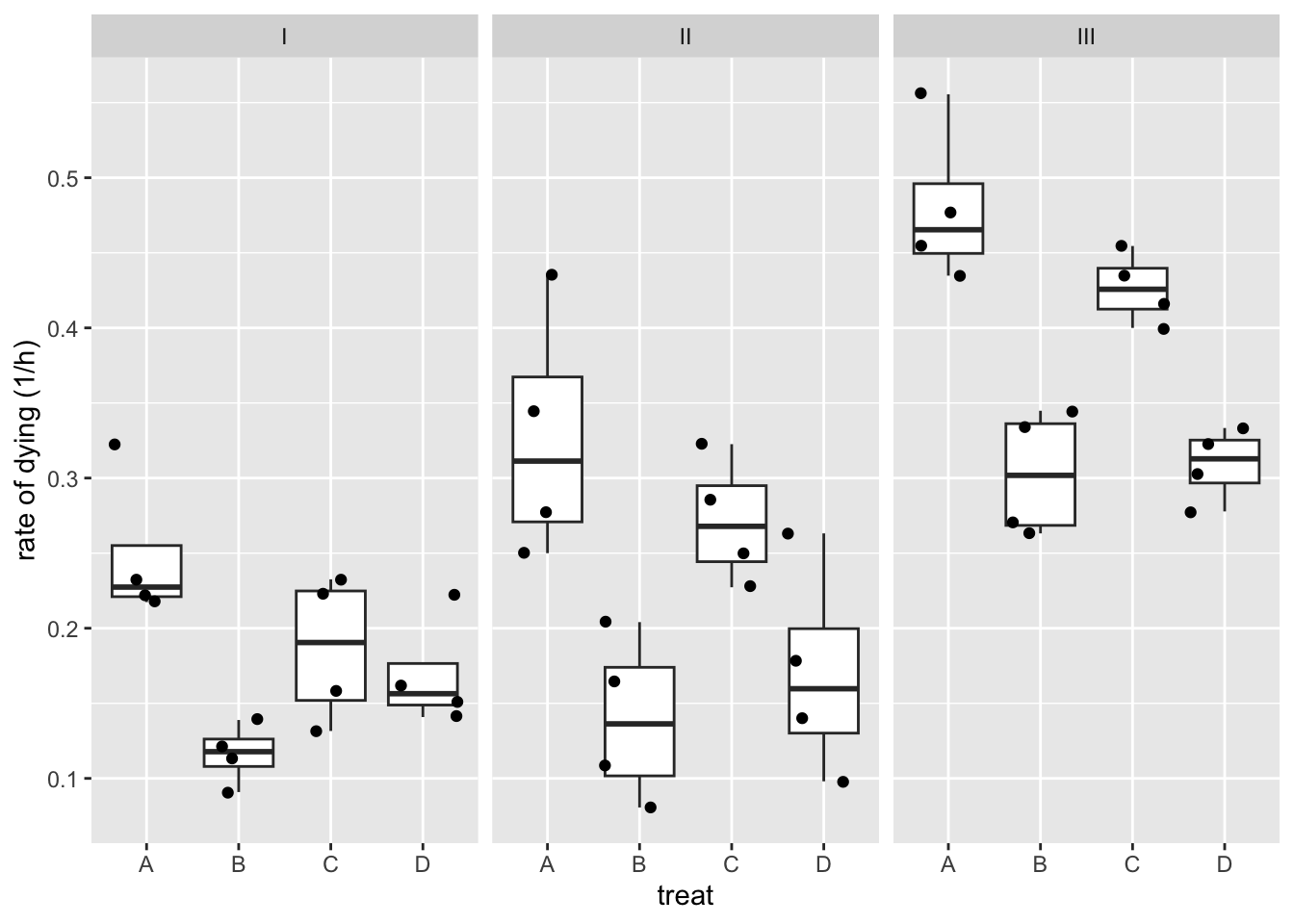

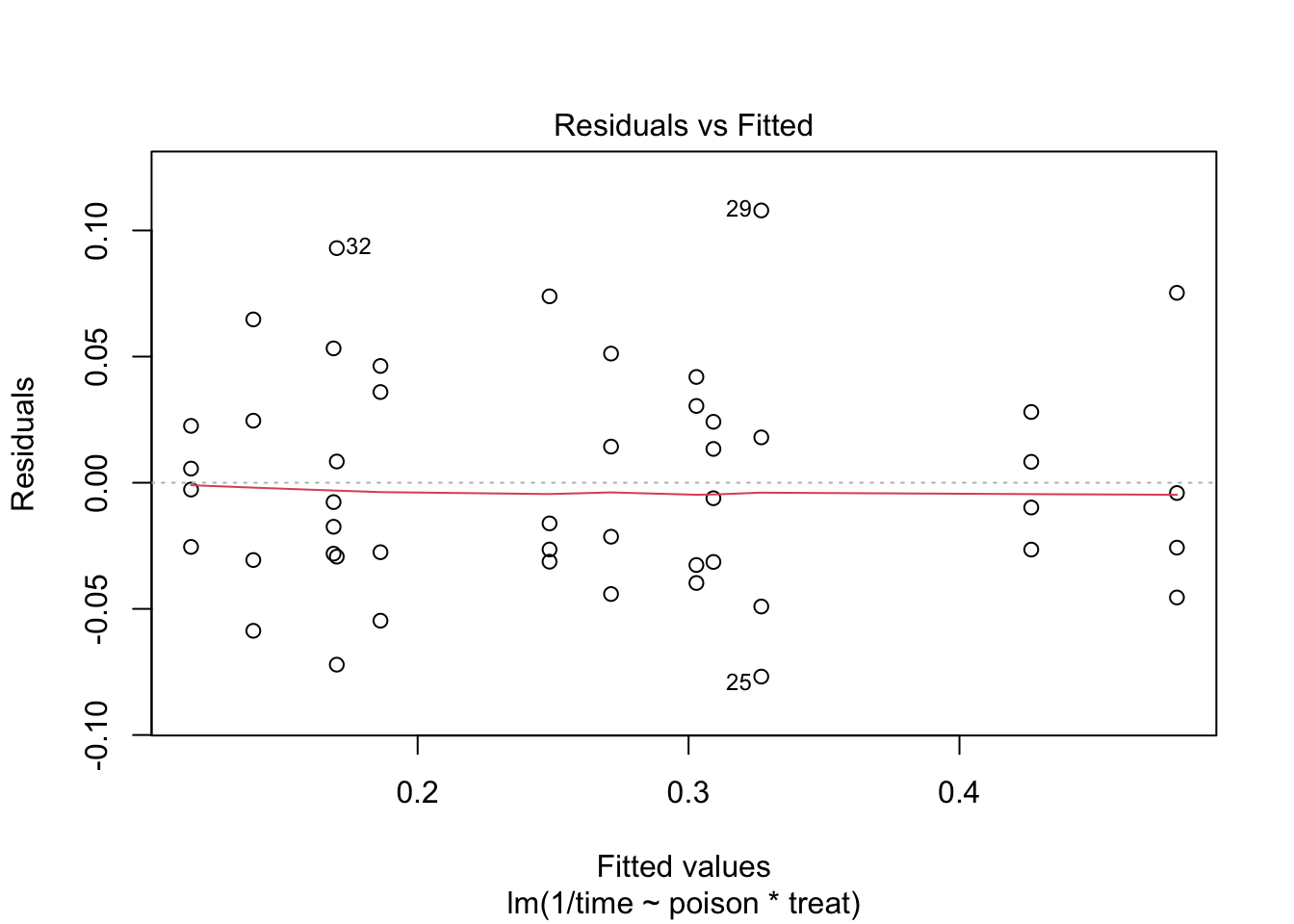
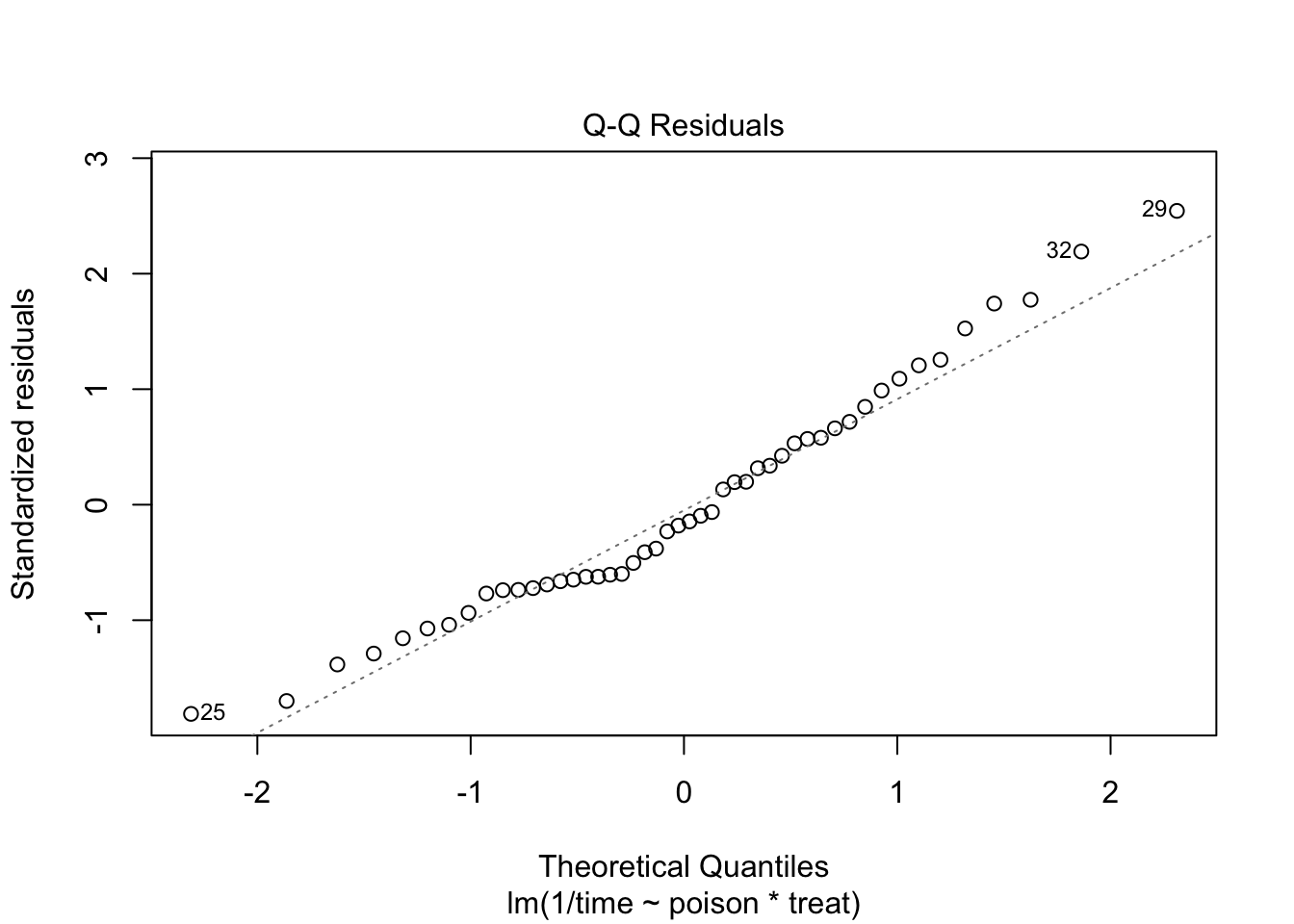
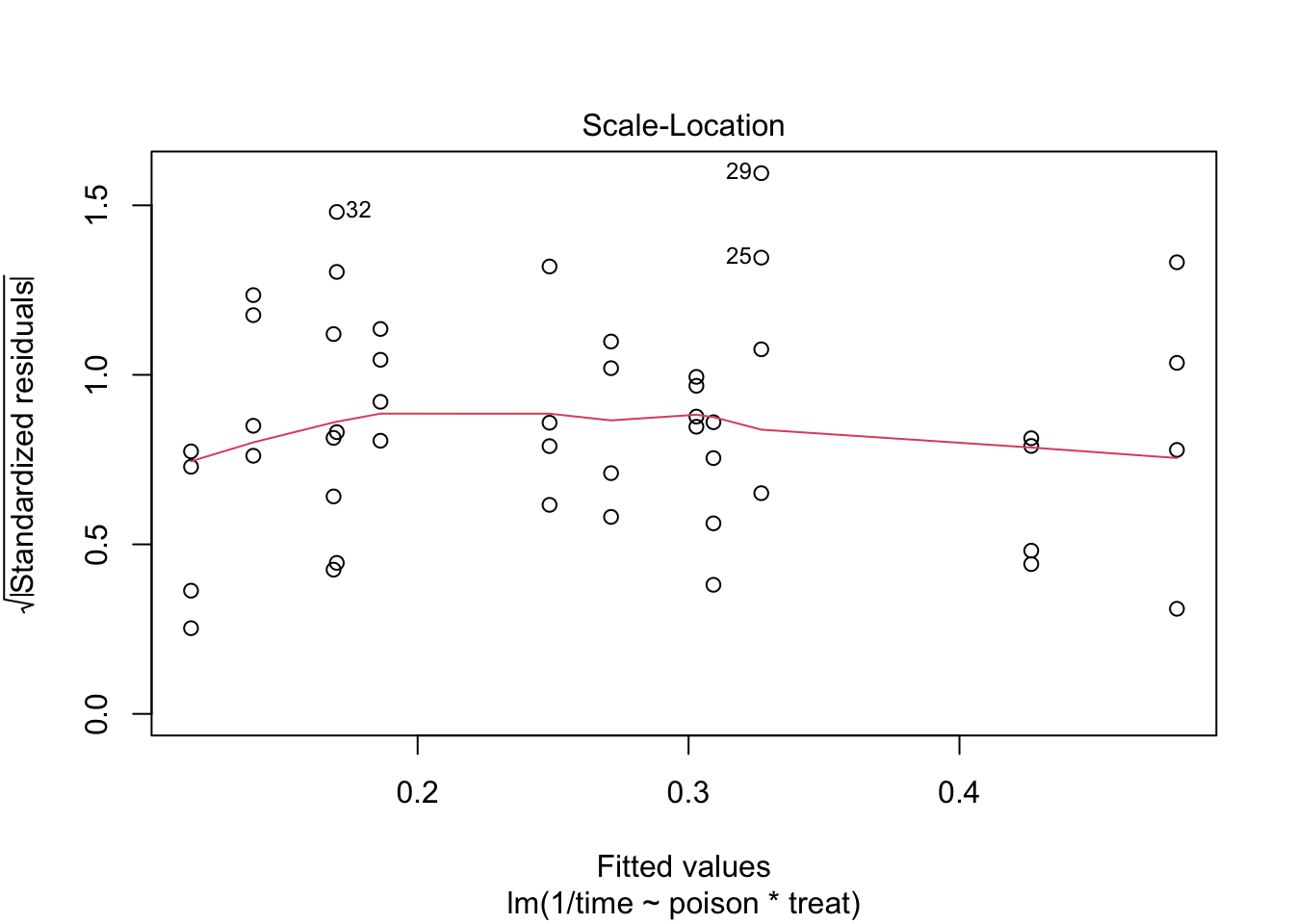
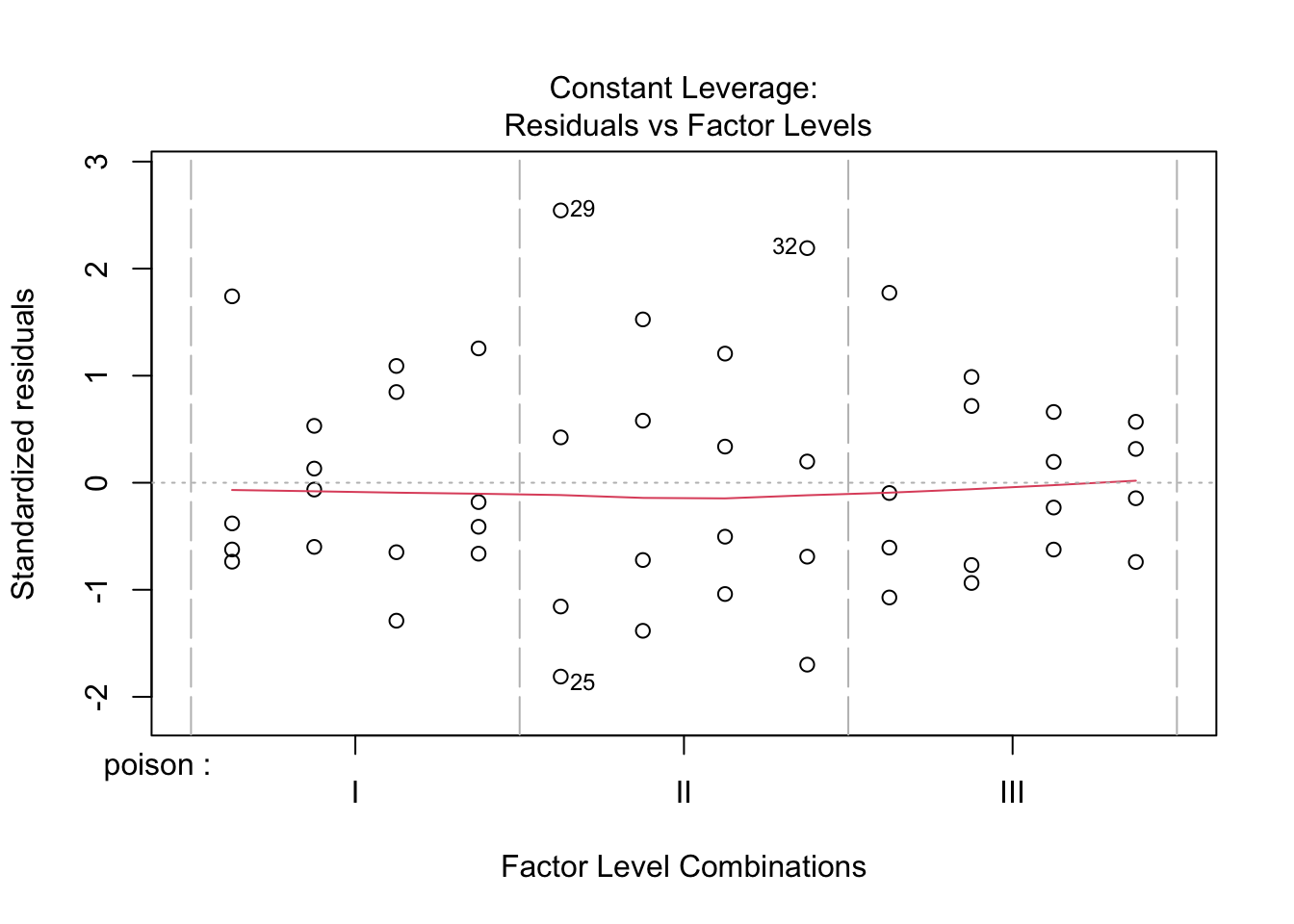
rats3 <- lm(1/time~poison*treat, rats)
plot(rats3) 

De reciproke transformatie lijkt beter. Transformaties bemoeilijken soms de interpretatie. Hier kan de reciproke transformatie echter worden geïnterpreteerd als de “snelheid van sterven” (rate of dying).

4 Inferentie

Er zijn meerdere interactie termen in het model. We kunnen deze eerst samen testen a.d.h.v. van de resultaten uit de anova tabel.

library(car)
Anova(rats3, type="III")

4.1 Verwijderen van niet-significante interactie.

De interactie tussen gif en behandeling is niet significant op het 5% niveau.

Een veelgebruikte methode is om de niet-significante interactie te verwijderen uit het model.

We verkrijgen dan een additief model wat toelaat om de effecten van de twee factoren afzonderlijk te bestuderen.

rats4 <- lm(1/time~poison + treat, rats)
plot(rats4)

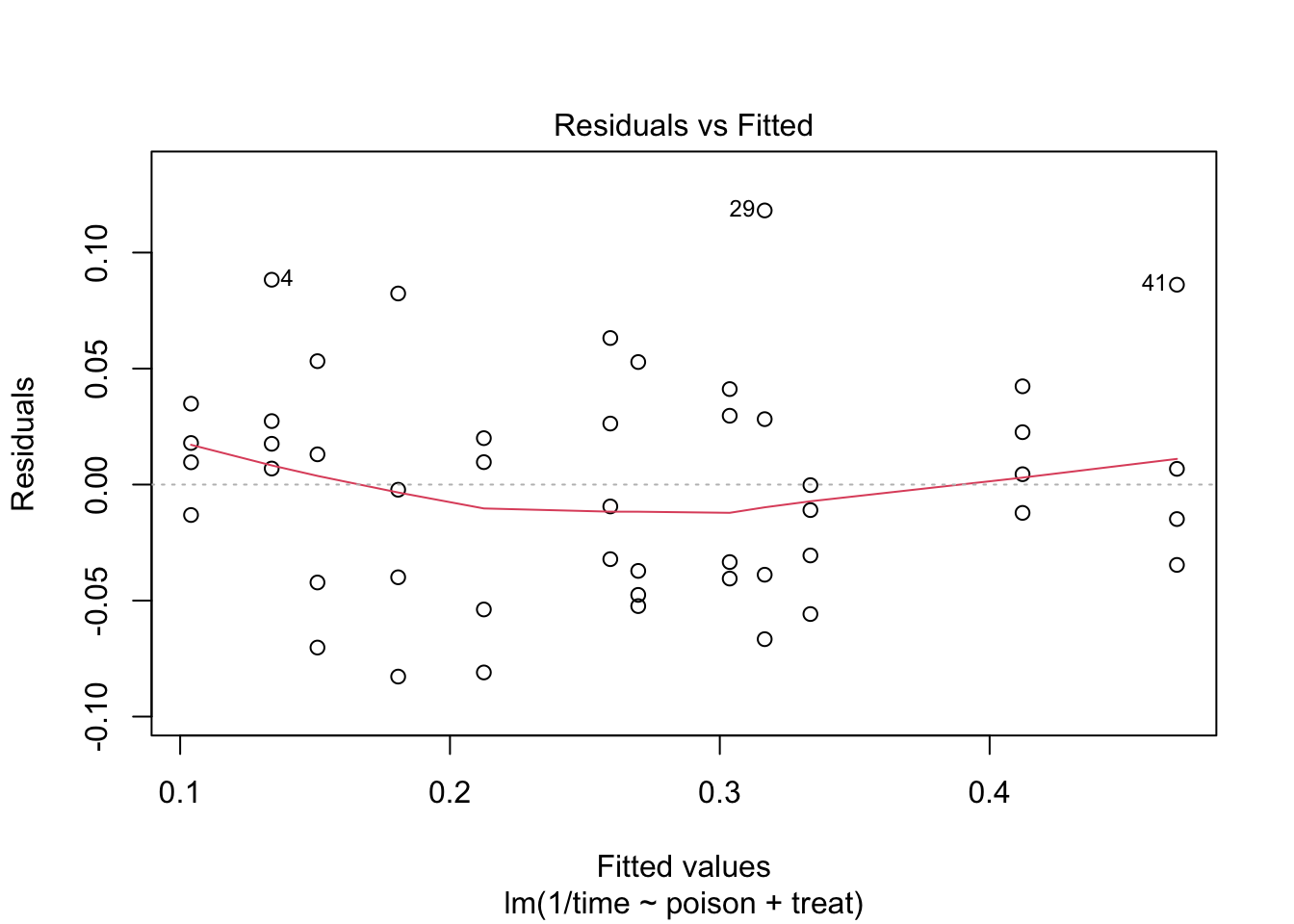
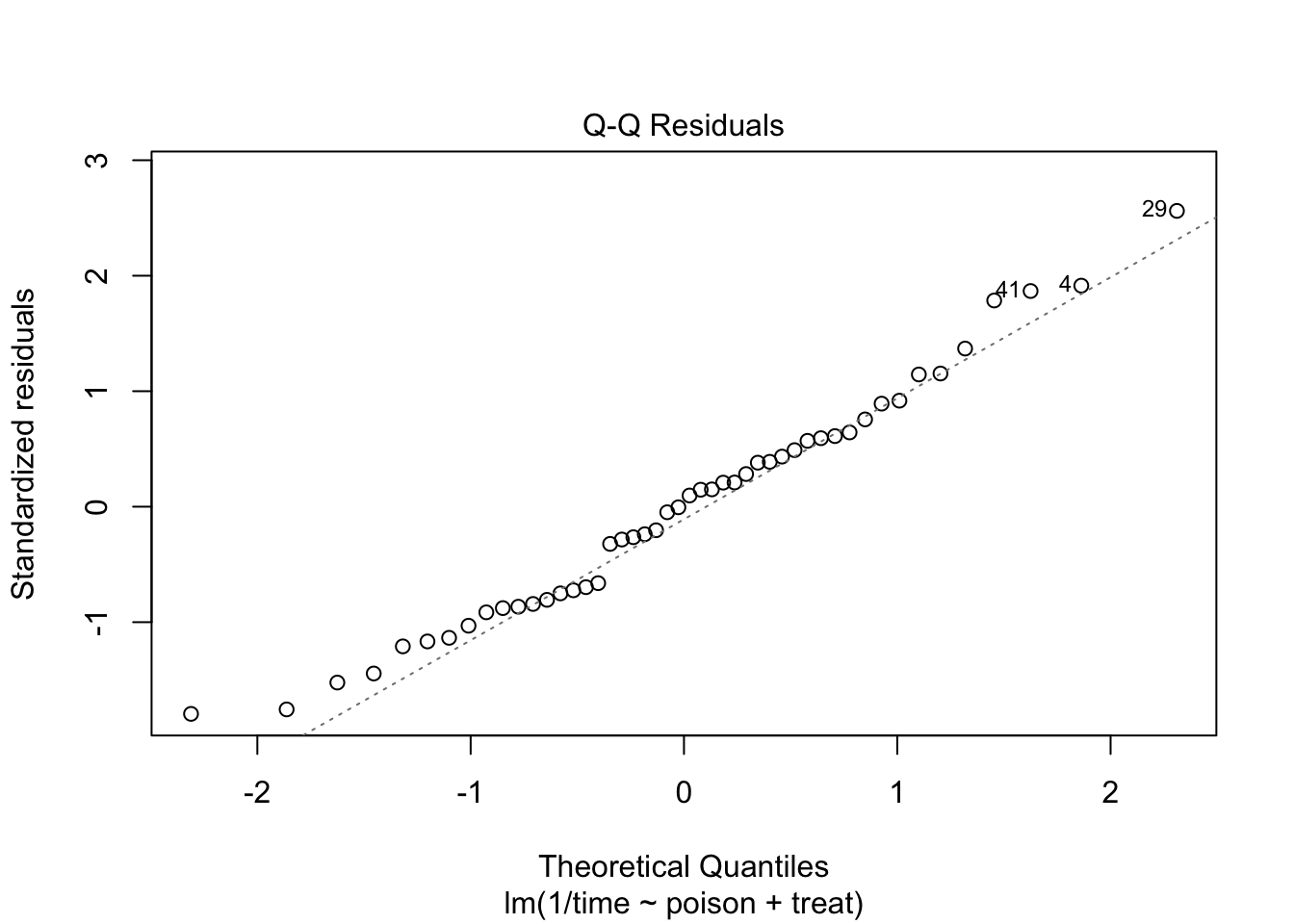
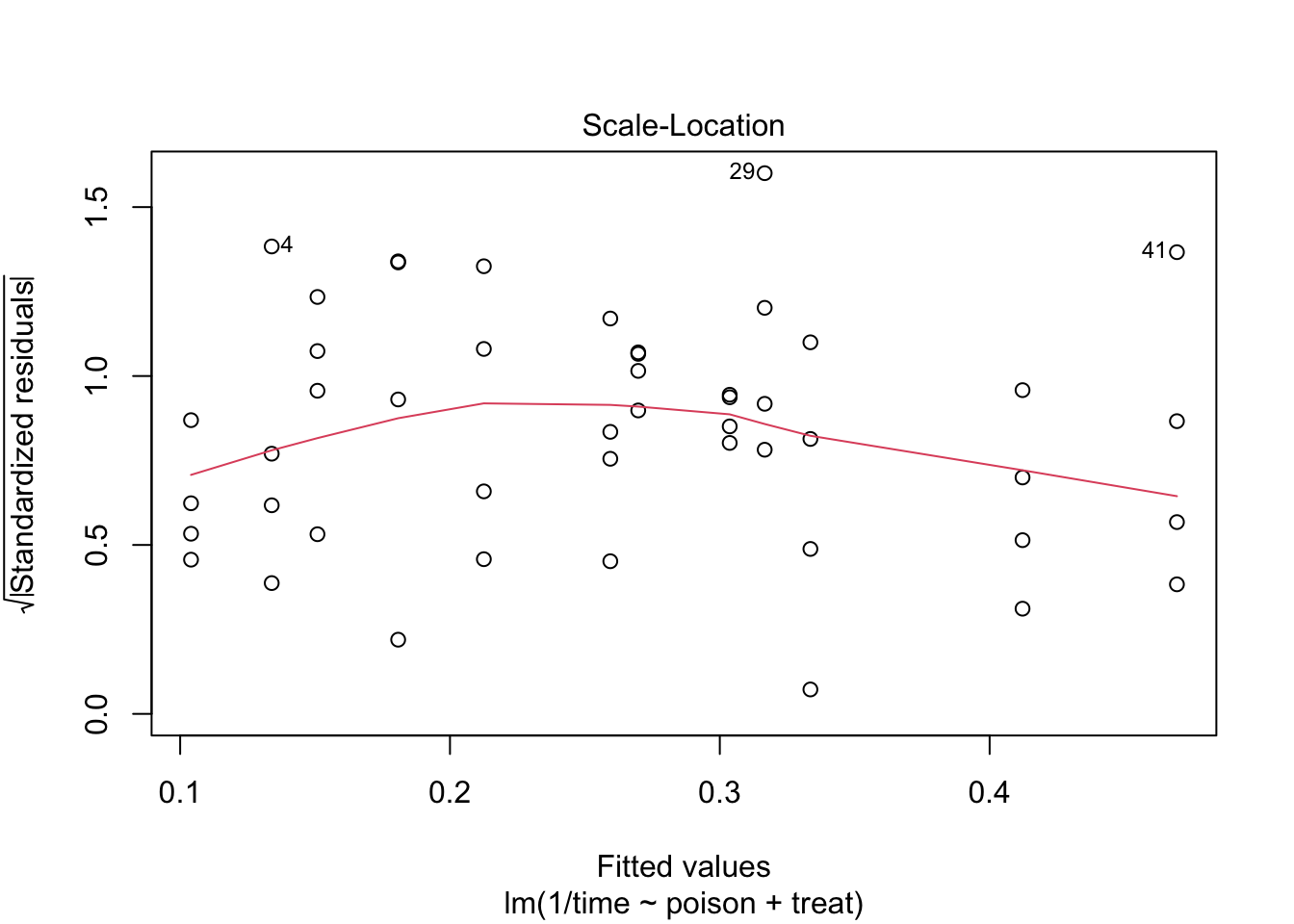
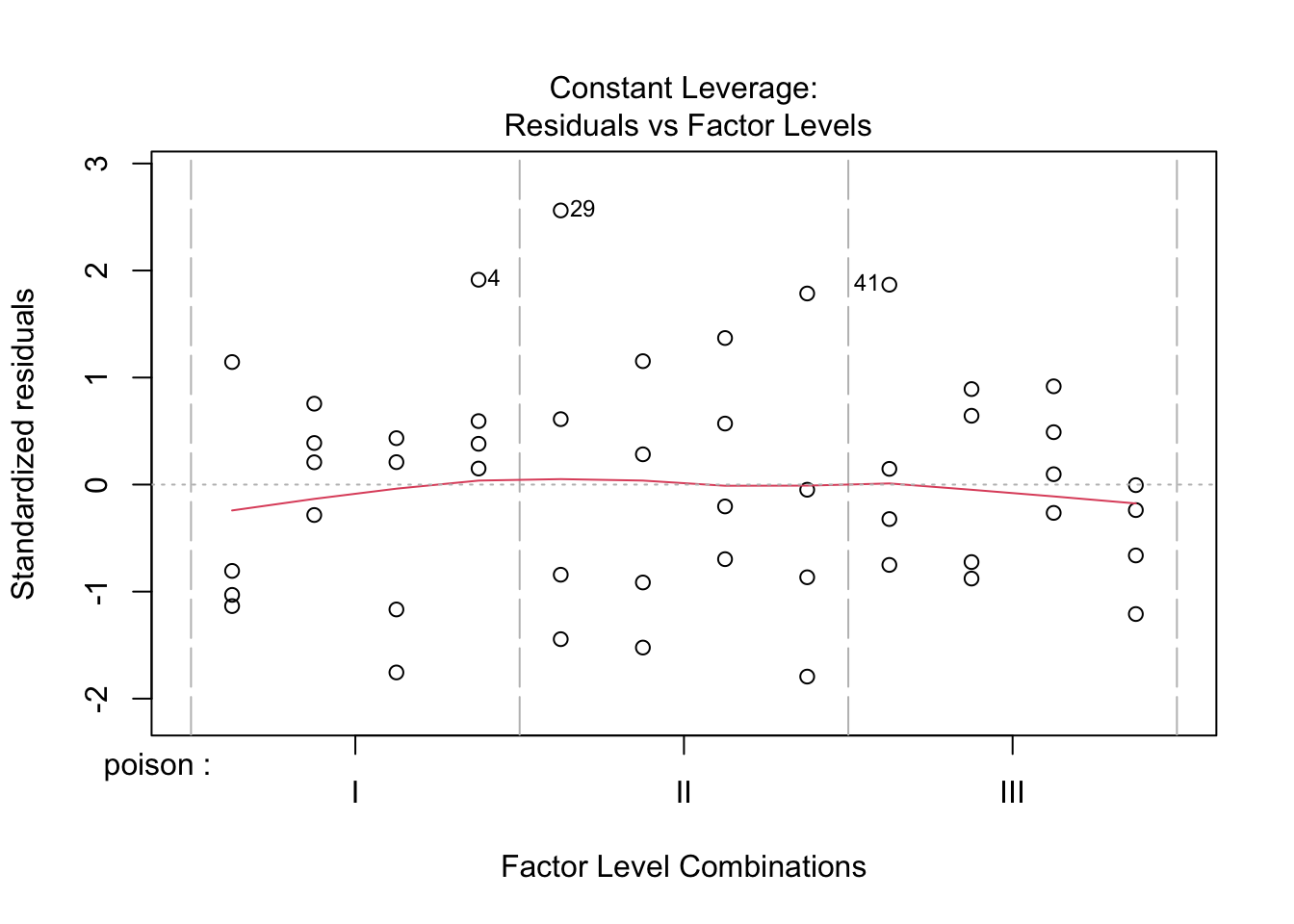
We zien wel iets meer afwijkingen in de residu plot.

Anova(rats4, type="III")

De anova tabel toont dat het effect van gif en behandeling beiden extreem siginficant zijn (beide \(p<< 0.001\)).

Het additieve model laat toe om de effecten van het type gif en de behandeling afzonderlijke te bestuderen via een post-hoc analyse.

library(multcomp)
comparisons <- glht(rats4, linfct = mcp(poison = "Tukey", treat="Tukey"))
summary(comparisons)

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = 1/time ~ poison + treat, data = rats)

Linear Hypotheses:
                      Estimate Std. Error t value Pr(>|t|)    
poison: II - I == 0    0.04686    0.01744   2.688  0.07353 .  
poison: III - I == 0   0.19964    0.01744  11.451  < 0.001 ***
poison: III - II == 0  0.15278    0.01744   8.763  < 0.001 ***
treat: B - A == 0     -0.16574    0.02013  -8.233  < 0.001 ***
treat: C - A == 0     -0.05721    0.02013  -2.842  0.05097 .  
treat: D - A == 0     -0.13583    0.02013  -6.747  < 0.001 ***
treat: C - B == 0      0.10853    0.02013   5.391  < 0.001 ***
treat: D - B == 0      0.02991    0.02013   1.485  0.61545    
treat: D - C == 0     -0.07862    0.02013  -3.905  0.00275 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

confint(comparisons)

     Simultaneous Confidence Intervals

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = 1/time ~ poison + treat, data = rats)

Quantile = 2.8494
95% family-wise confidence level
 

Linear Hypotheses:
                      Estimate   lwr        upr       
poison: II - I == 0    0.0468641 -0.0028153  0.0965435
poison: III - I == 0   0.1996425  0.1499631  0.2493219
poison: III - II == 0  0.1527784  0.1030990  0.2024578
treat: B - A == 0     -0.1657402 -0.2231051 -0.1083754
treat: C - A == 0     -0.0572135 -0.1145784  0.0001513
treat: D - A == 0     -0.1358338 -0.1931987 -0.0784690
treat: C - B == 0      0.1085267  0.0511619  0.1658915
treat: D - B == 0      0.0299064 -0.0274584  0.0872712
treat: D - C == 0     -0.0786203 -0.1359851 -0.0212555

plot(comparisons,yaxt="none")
contrastNames <- c("II-I","III-I","III-II","B-A","C-A","D-A","C-B","D-B","D-C")
axis(2,at=c(length(contrastNames):1), labels=contrastNames,las=2)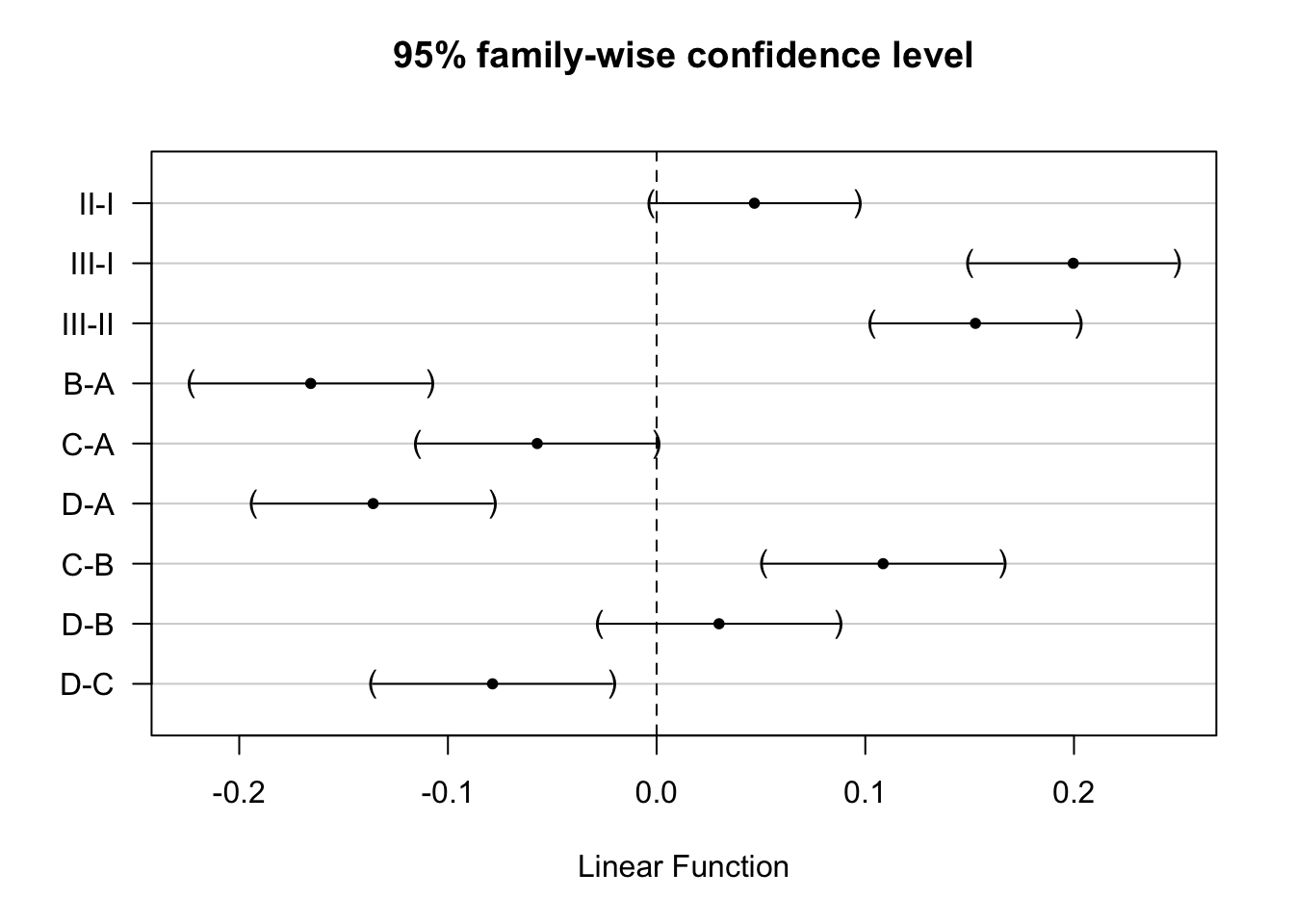

4.2 Niet-significante interactie term in het model weerhouden

Het aanvaarden van de null hypothese dat er geen interactie is, is een zwakke conclusie. Het zou immers kunnen dat de power van het experiment te klein is om de interactie op te pikken. We kunnen er ook voor kiezen om de niet significante interactie term in het model te laten.

Als de interactie significant zou zijn geweest, betekent dit dat het effect van het gif op de snelheid van sterven afhangt van de behandeling en vice versa. Dan kunnen we het effect van het type gif en de behandeling op de overlevingstijd niet afzonderlijk bestuderen.

ExploreModelMatrix::VisualizeDesign(rats,~poison*treat)$plot

[[1]]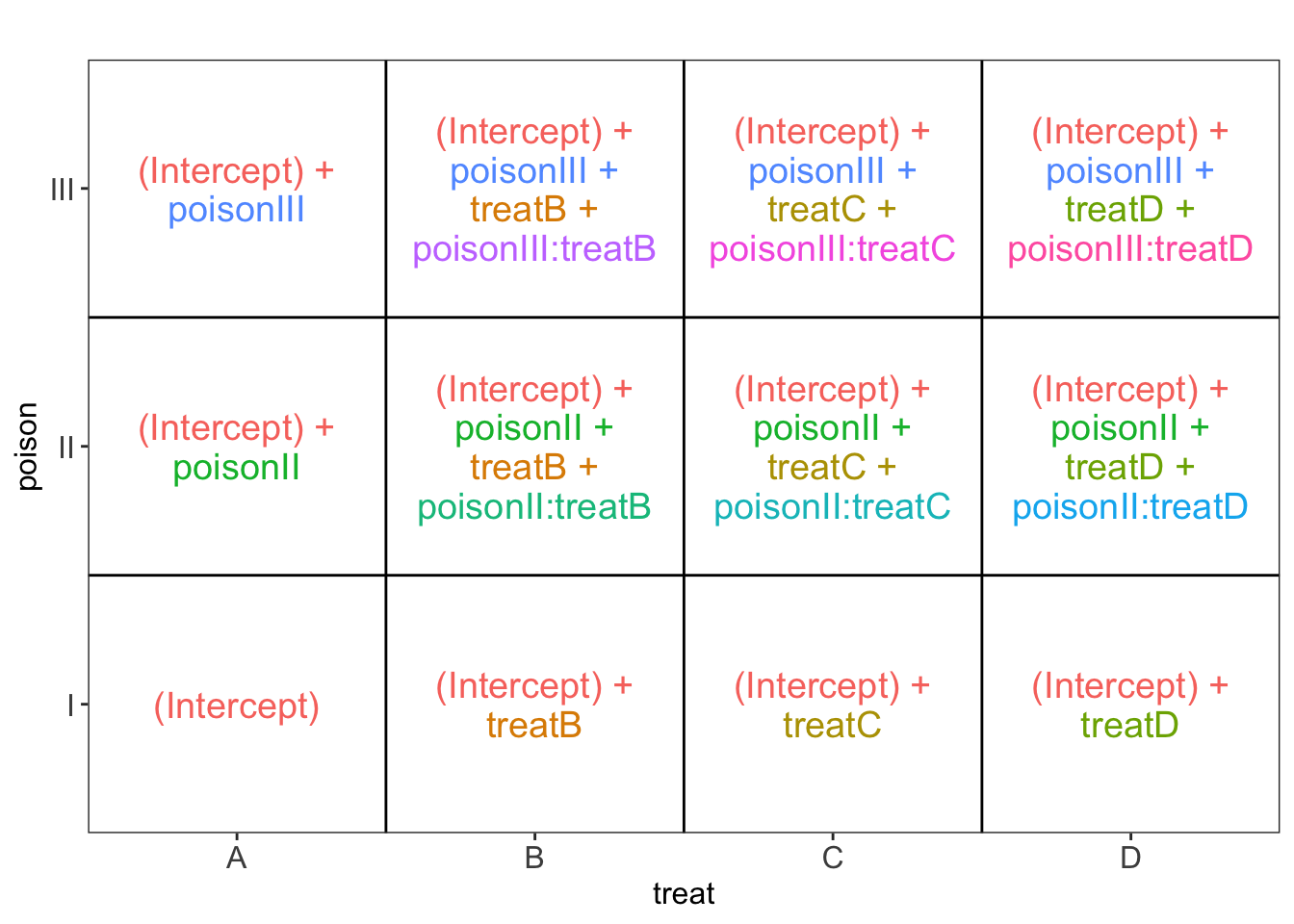

We zouden dan het effect van het type gif afzonderlijk moeten bestuderen voor elke behandeling:

1. Voor behandeling A moeten we dan volgende nulhypotheses toetsen:

• II-I: \(H_0: \beta_{II}=0\)
• III-I: \(H_0: \beta_{III}=0\)
• III-II: \(H_0: \beta_{III}-\beta_{II}=0\)

2. Voor behandeling B:

• II-I: \(H_0: \beta_{II}+\beta_{II:B}=0\)
• III-I: \(H_0: \beta_{III}+\beta_{III:B}=0\)
• III-II: \(H_0: \beta_{III}+\beta_{III:B}-\beta_{II}-\beta_{II:B}=0\)

3. Voor behandeling C:

• II-I: \(H_0: \beta_{II}+\beta_{II:C}=0\)
• III-I: \(H_0: \beta_{III}+\beta_{III:C}=0\)
• III-II: \(H_0: \beta_{III}+\beta_{III:C}-\beta_{II}-\beta_{II:C}=0\)

4. Voor behandeling D:

• II-I: \(H_0: \beta_{II}+\beta_{II:D}=0\)
• III-I: \(H_0: \beta_{III}+\beta_{III:D}=0\)
• III-II: \(H_0: \beta_{III}+\beta_{III:D}-\beta_{II}-\beta_{II:D}=0\)

Het zelfde geldt wanneer we het effect van de behandeling bestuderen:

1. Voor gif I toetsen we dan nulhypothese

• B-A: \(H_0: \beta_{B}=0\)
• C-A: \(H_0: \beta_{C}=0\)
• D-A: \(H_0: \beta_{D}=0\)
• C-B: \(H_0: \beta_{C}-\beta_{B}=0\)
• D-B: \(H_0: \beta_{D}-\beta_{B}=0\)
• D-C: \(H_0: \beta_{D}-\beta_{C}=0\)

2. Gif II

• B-A: \(H_0: \beta_{B}+\beta_{II:B}=0\)
• C-A: \(H_0: \beta_{C}+\beta_{II:C}=0\)
• D-A: \(H_0: \beta_{D}+\beta_{II:D}=0\)
• C-B: \(H_0: \beta_{C}+\beta_{II:C}-\beta_{B}-\beta_{II:B}=0\)
• D-B: \(H_0: \beta_{D}+\beta_{II:D}-\beta_{B}-\beta_{II:B}=0\)
• D-C: \(H_0: \beta_{D}+\beta_{II:D}-\beta_{C}-\beta_{II:C}=0\)

3. Gif III

• B-A: \(H_0: \beta_{B}+\beta_{III:B}=0\)
• C-A: \(H_0: \beta_{C}+\beta_{III:C}=0\)
• D-A: \(H_0: \beta_{D}+\beta_{II:D}=0\)
• C-B: \(H_0: \beta_{C}+\beta_{III:C}-\beta_{B}-\beta_{III:B}=0\)
• D-B: \(H_0: \beta_{D}+\beta_{III:D}-\beta_{B}-\beta_{III:B}=0\)
• D-C: \(H_0: \beta_{D}+\beta_{III:D}-\beta_{C}-\beta_{III:C}=0\)

comparisonsInt <- glht(rats3, linfct = c(
  "poisonII = 0",
  "poisonIII = 0",
  "poisonIII - poisonII = 0",
  "poisonII + poisonII:treatB = 0",
  "poisonIII + poisonIII:treatB = 0",
  "poisonIII + poisonIII:treatB - poisonII- poisonII:treatB = 0",  
  "poisonII + poisonII:treatC = 0",
  "poisonIII + poisonIII:treatC = 0",
  "poisonIII + poisonIII:treatC - poisonII- poisonII:treatC = 0",  
  "poisonII + poisonII:treatD = 0",
  "poisonIII + poisonIII:treatD = 0",
  "poisonIII + poisonIII:treatD - poisonII- poisonII:treatD = 0",  
  "treatB = 0",
  "treatC = 0",
  "treatD = 0",
  "treatC - treatB = 0",
  "treatD - treatB = 0",
  "treatD - treatC = 0",
  "treatB + poisonII:treatB = 0",
  "treatC + poisonII:treatC = 0",
  "treatD + poisonII:treatD = 0",
  "treatC + poisonII:treatC - treatB - poisonII:treatB = 0",
  "treatD + poisonII:treatD - treatB - poisonII:treatB = 0",
  "treatD + poisonII:treatD - treatC - poisonII:treatC = 0",
  "treatB + poisonIII:treatB = 0",
  "treatC + poisonIII:treatC = 0",
  "treatD + poisonIII:treatD = 0",
  "treatC + poisonIII:treatC - treatB - poisonIII:treatB = 0",
  "treatD + poisonIII:treatD - treatB - poisonIII:treatB = 0",
  "treatD + poisonIII:treatD - treatC - poisonIII:treatC = 0")
)

contrastNames<-
  c(paste(rep(LETTERS[1:4],each=3),rep(apply(combn(c("I","II","III"),2)[2:1,],2,paste,collapse="-") ,4),sep=": "),
    paste(rep(c("I","II","III"),each=6),rep(apply(combn(c(LETTERS[1:4]),2)[2:1,],2,paste,collapse="-") ,3),sep=": "))

plot(comparisonsInt,yaxt="none")
axis(2,at=c(length(contrastNames):1), labels=contrastNames,las=2)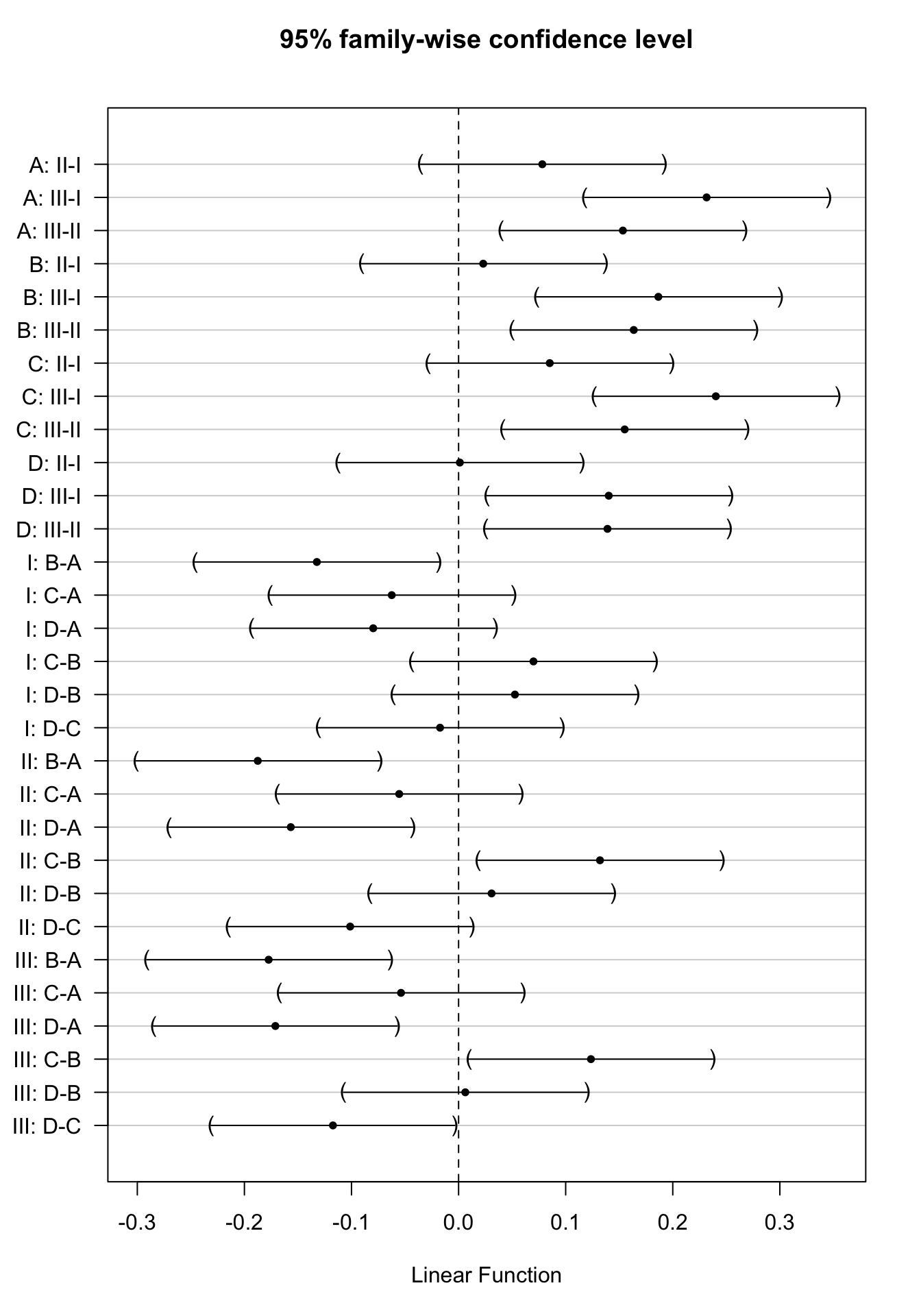

In onze studie was de interactie echter niet significant. Het effect van het gif (II-I, III-I en III- II) verandert dus niet significant volgens de behandeling (A, B, C, en D) en vice versa. Voor onze dataset lijkt het dus zinvol om

1. de effectgrootte voor de pairsgewijze vergelijkingen tussen de verschillende giffen (II-I, III-I en III- II) te schatten door ze uit te middelen over alle behandelingen (A, B, C, en D), en,
2. de effectgrootte voor de pairsgewijze vergelijkingen tussen de verschillende behandelingen (B-A, C-A, D-A, C-B, D-B en D-C) te schatten door ze uit te middelen over alle giffen (I, II, III).

Dat zou ons gelijkaardige schattingen van de effectgroottes moeten geven als deze voor het additieve model waarbij we de interactie term uit het model hadden geweerd.

B.v. voor gif III vs gif II zou dat in volgende contrast resulteren:

• III-II: \[H_0: \begin{array}{l} \frac{\beta_{III}-\beta_{II}}{4} + \\ \quad \frac{\beta_{III} + \beta_{III:B}-\beta_{II} - \beta_{II:B}}{4} + \\ \quad \quad \frac{\beta_{III} + \beta_{III:C}-\beta_{II} - \beta_{II:C}}{4} + \\ \quad \quad \quad \frac{\beta_{III} + \beta_{III:D}-\beta_{II} - \beta_{II:D}}{4}=0 \end{array} \] \[ H_0:\beta_{III} + \frac{1}{4} \times \beta_{III:B} + \frac{1}{4} \times\beta_{III:C} + \frac{1}{4} \times\beta_{III:D} -\beta_{II} - \frac{1}{4} \times\beta_{II:B} - \frac{1}{4} \times\beta_{II:C} - \frac{1}{4} \times\beta_{II:D}=0 \]

We schatten met onderstaande code alle gemiddelde contrasten a.d.h.v. het model met interactie.

contrasts <- c(
  "poisonII + 1/4*poisonII:treatB + 1/4*poisonII:treatC + 1/4*poisonII:treatD = 0",
  "poisonIII + 1/4*poisonIII:treatB + 1/4*poisonIII:treatC + 1/4*poisonIII:treatD= 0",
  "poisonIII + 1/4*poisonIII:treatB + 1/4*poisonIII:treatC + 1/4*poisonIII:treatD - poisonII - 1/4*poisonII:treatB - 1/4*poisonII:treatC - 1/4*poisonII:treatD = 0",
  "treatB + 1/3*poisonII:treatB + 1/3*poisonIII:treatB = 0",
  "treatC + 1/3*poisonII:treatC + 1/3*poisonIII:treatC = 0",
  "treatD + 1/3*poisonII:treatD + 1/3*poisonIII:treatD = 0",
  "treatC + 1/3*poisonII:treatC + 1/3*poisonIII:treatC - treatB - 1/3*poisonII:treatB - 1/3*poisonIII:treatB = 0",
  "treatD + 1/3*poisonII:treatD + 1/3*poisonIII:treatD  - treatB - 1/3*poisonII:treatB - 1/3*poisonIII:treatB = 0",
  "treatD + 1/3*poisonII:treatD + 1/3*poisonIII:treatD  - treatC - 1/3*poisonII:treatC - 1/3*poisonIII:treatC = 0") 


comparisonsInt2 <- glht(rats3, linfct = contrasts
)
plot(comparisonsInt2,yaxt="none")
contrastNames <- c("II-I","III-I","III-II","B-A","C-A","D-A","C-B","D-B","D-C")
axis(2,at=c(length(contrastNames):1), labels=contrastNames,las=2)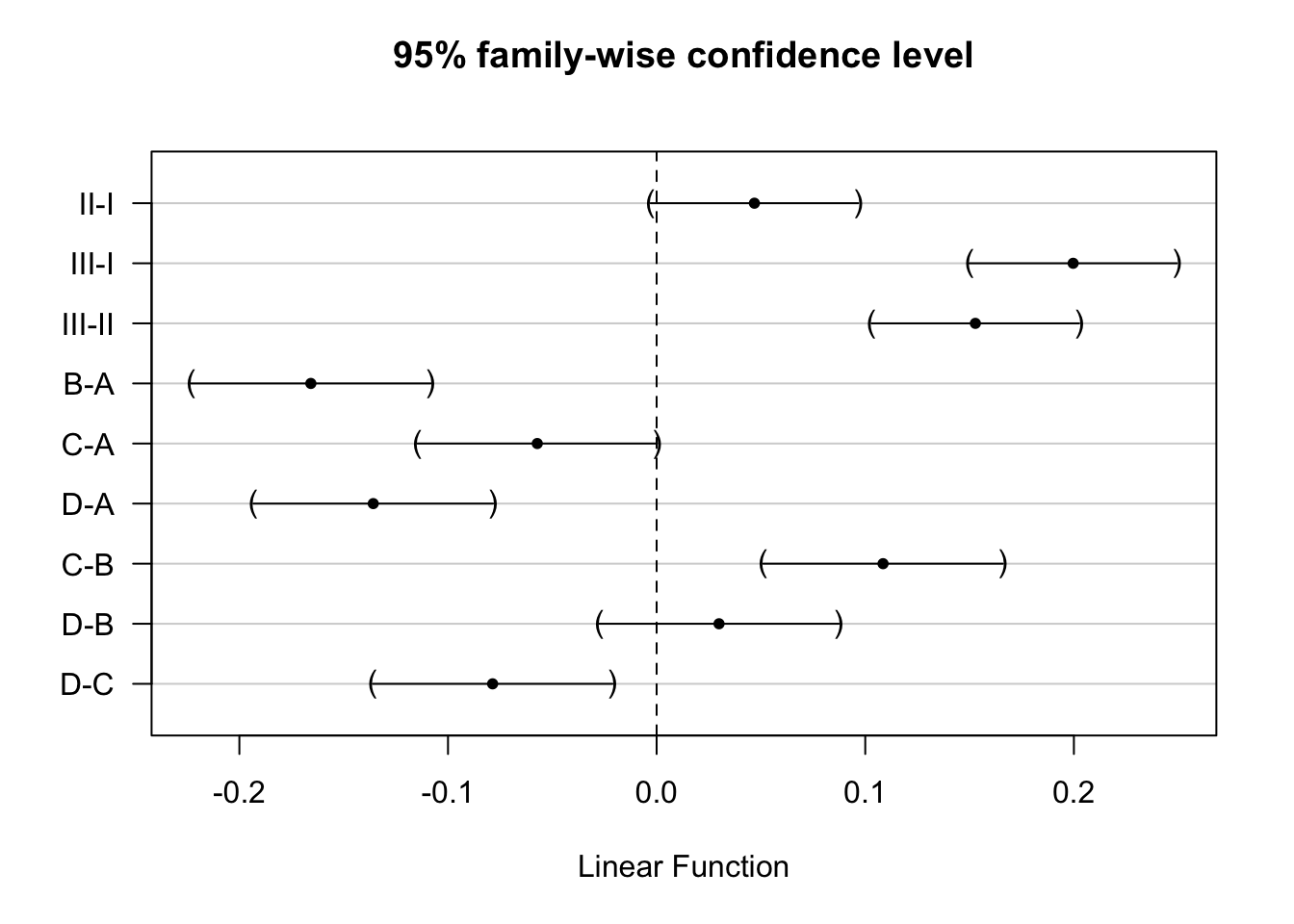

De geschatte effectgroottes zijn inderdaad exact gelijk als bij het model zonder interactie omdat het experiment gebalanceerd is.

De standaard errors verschillen wel lichtjes. Dat is het gevolg van de errors die verschillen tussen beiden modellen alsook het aantal vrijheidsgraden van de errors (n-p).

data.frame(Additive_coef=summary(comparisons)$test$coef,Additive_se=summary(comparisons)$test$sigma,Int_coef=summary(comparisonsInt2)$test$coef,int_se=summary(comparisonsInt2)$test$sigma) %>% round(3)

5 Conclusie

Er is een extreem significant effect van het type gif en de behandeling op de snelheid van sterven bij ratten (p << 0.001).

De interactie tussen gif en behandeling is niet significant (p = 0.387).

De snelheid van sterven is gemiddeld 0.2h\(^{-1}\) en 0.15h\(^{-1}\) hoger voor ratten die blootgesteld worden aan gif III dan aan respectievelijk gif I en II (beide p << 0.001, 95% BI III-I: [0.15, 0.25]h\(^{-1}\), 95% BI III-II: [0.1, 0.2]h\(^{-1}\)) De gemiddelde snelheid van sterven was niet significant verschillend tussen ratten die werden blootgesteld aan gif I en gif II (p=0.074).

De snelheid van sterven is gemiddeld 0.17h\(^{-1}\) en 0.14h\(^{-1}\) hoger na behandeling A dan na behandeling B en D (p << 0.001, 95% BI B-A: [-0.22, -0.11]h\(^{-1}\), 95% BI D-A: [-0.19, -0.08]h\(^{-1}\)). De snelheid van sterven is gemiddeld 0.11h\(^{-1}\) en 0.08h\(^{-1}\) hoger na behandeling C dan respectievelijk na behandeling B en D (C-B: p << 0.001, 95% CI [0.05, 0.17]h\(^{-1}\) , D-C: p = 0.003, 95% CI [-0.14, -0.02]h\(^{-1}\)). De gemiddelde snelheid van sterven is niet significant verschillend tussen ratten behandeld met behandeling C vs A, en D vs B (p- waarden respectievelijk p = 0.051 en p = 0.61).

Alle p-waarden werden gecorrigeerd voor meervoudig testen.

---

This work is licensed under the CC BY-NC-SA 4.0 licence.