Exercise 5.2: Hypothesis testing on the pertussis example - solution

1 Aim of this tutorial

Upon this exercise you can

1. conduct a statistical hypothesis test for a two group comparison in R and to interpret the results.
2. critically evaluate the assumptions for a two sample t-test
3. use simulations to assist you when evaluating the assumptions of a two group comparison
4. select the correct test based on the data exploration.

2 Background

Researchers wanted to study the immune response on pertussis. They have set up an experiments with 40 rats. 16 rats were infected with pertussis and 24 rats received a control treatment. Researchers measured the white blood cell concentration (WBC) in each rat (count per mm\(^3\)).

De data consists of two variables:

• WBC: white blood cell count (counts/mm\(^3\)).

• trt: treatment

  • control: rat recieved control treatment
  • pertussis: rat was infected with pertussis

3 Import the dataset

Load the libraries

library(tidyverse)

Data path:

https://raw.githubusercontent.com/statOmics/PSLSData/main/wbcon.csv

wbcon <- read_csv("https://raw.githubusercontent.com/statOmics/PSLSData/main/wbcon.csv")

## Rows: 40 Columns: 2
## ── Column specification ──────────────────────────────────────────────
## Delimiter: ","
## chr (1): trt
## dbl (1): WBC
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

glimpse(wbcon)

## Rows: 40
## Columns: 2
## $ WBC <dbl> 10252, 10467, 10601, 10638, 10901, 11071, 11092, 11371, …
## $ trt <chr> "control", "control", "control", "control", "control", "…

3.1 Aim of the study

The overarching goal of this study was to assess if the white blood cell count changes upon pertussis infection. To this end, researchers randomized 40 rats to two treatments: A control treatment and a treatment in which the rat was infected with pertussis.

4 Data exploration

A crucial first step in a data analysis is to visualize and to explore the raw data.

This will allow us to gain insight in the data.

A secondary goal of the data exploration is to check the assumptions of the test that we will perform.

4.1 Which test will you perform to compare the white blood cell count between infected and control rats?

40 different rats are assigned at random to a control treatment or a treatment where they are infected with pertussis. The white blood cells of the rats are measured on different animals and we can assume that the data between rats are independent. Note, that this will not be the case if multiple rats are housed in the same cages!

We will therefore perform a two-sample t-test to assess if the average white blood cell count differs between infected rats and rats that received the control treatment.

4.2 What are the assumptions of this test?

1. The data are independent
2. The data in both groups have the same variance
3. The data in both groups are normally distributed.

4.3 Boxplots

We can assess the second assumption using boxplots.

wbcon %>% ggplot(aes(x = trt, y = WBC, fill = trt)) +
  geom_boxplot(outlier.shape = NA) +
  geom_point(position = "jitter") +
  ylab("WBC (count/mm3)") +
  xlab("treatment") +
  stat_summary(
    fun = mean, geom = "point",
    shape = 5, size = 3, color = "black"
  )

What do you observe?

Both the mean and variance of the data seems to differ between control rats and rats infected with pertussis. So the second assumption is not valid. If the data are normally distributed we can compare the groups using a Welch modified t-test, which is valid if the data in both groups are exhibiting a different variance.

4.4 QQ-plots

To assess the assumption that the data are normally distributed in each treatment group, we will use QQ plots.

wbcon %>%
  ggplot(aes(sample = WBC)) +
  geom_qq() +
  geom_qq_line() +
  facet_grid(cols = vars(trt))

What do you observe?

The white blood cell counts appear to be normally distributed in both treatment groups.

5 Assess the research question with the appropriate t-test

5.1 Analysis

output <- t.test(WBC ~ trt, data = wbcon, var.equal = FALSE)
output

## 
##  Welch Two Sample t-test
## 
## data:  WBC by trt
## t = -5.7114, df = 15.132, p-value = 3.984e-05
## alternative hypothesis: true difference in means between group control and group pertussis is not equal to 0
## 95 percent confidence interval:
##  -32311.32 -14758.47
## sample estimates:
##   mean in group control mean in group pertussis 
##                12215.92                35750.81

5.2 Conclusion

The average white blood cell count is extremely different between rats that are infected with pertussis and rads that received a control treatment (p << 0.001).

The white blood cell count is on average 23535 blood cells/mm\(^3\) higher for rats with pertussis than for rats that received a control treatment (95% CI [14758, 32311]).

6 ADDENDUM: Train yourself in checking the assumptions

In order for the learners to get more proficient in evaluating the assumptions we will simulate 8 dataset with sample sizes similar to our data for which the assumptions of normality and equal variance do hold. For the QQ-plots we will only plot the one from one of the groups.

6.1 Simulate data

We simulate 8 datasets with the same sample sizes, means and pooled variance as in the sample.

set.seed(21532)
nSim <- 8
## descriptive statistics
wbcSum <- wbcon %>%
  group_by(trt) %>%
  summarize(
      mean = mean(WBC, na.rm = TRUE),
      sd = sd(WBC, na.rm = TRUE),
      n = n()
  ) %>%
  mutate(se = sd / sqrt(n))

sigma <- sqrt(sum(wbcSum$sd^2 * (wbcSum$n - 1)) / (sum(wbcSum$n) - 2))

normSim <- matrix(
  c(
    wbcon$WBC,
    rnorm(sum(wbcSum$n) * nSim,
          mean = c(
            rep(wbcSum$mean[1], wbcSum$n[1]),
            rep(wbcSum$mean[2], wbcSum$n[2])
            ),
          sd = sigma)
    ),
  nrow = sum(wbcSum$n)) %>%
  as.data.frame() %>%
  mutate(trt = wbcon$trt)

6.2 Comparisons of variances

names(normSim)[1:(nSim+1)] <- c("orig",paste0("sim",1:nSim))
normSim %>%
  gather(samp, data, -trt) %>%
  ggplot(aes(x = trt, y = data)) +
  geom_boxplot() +
  facet_wrap(~samp)

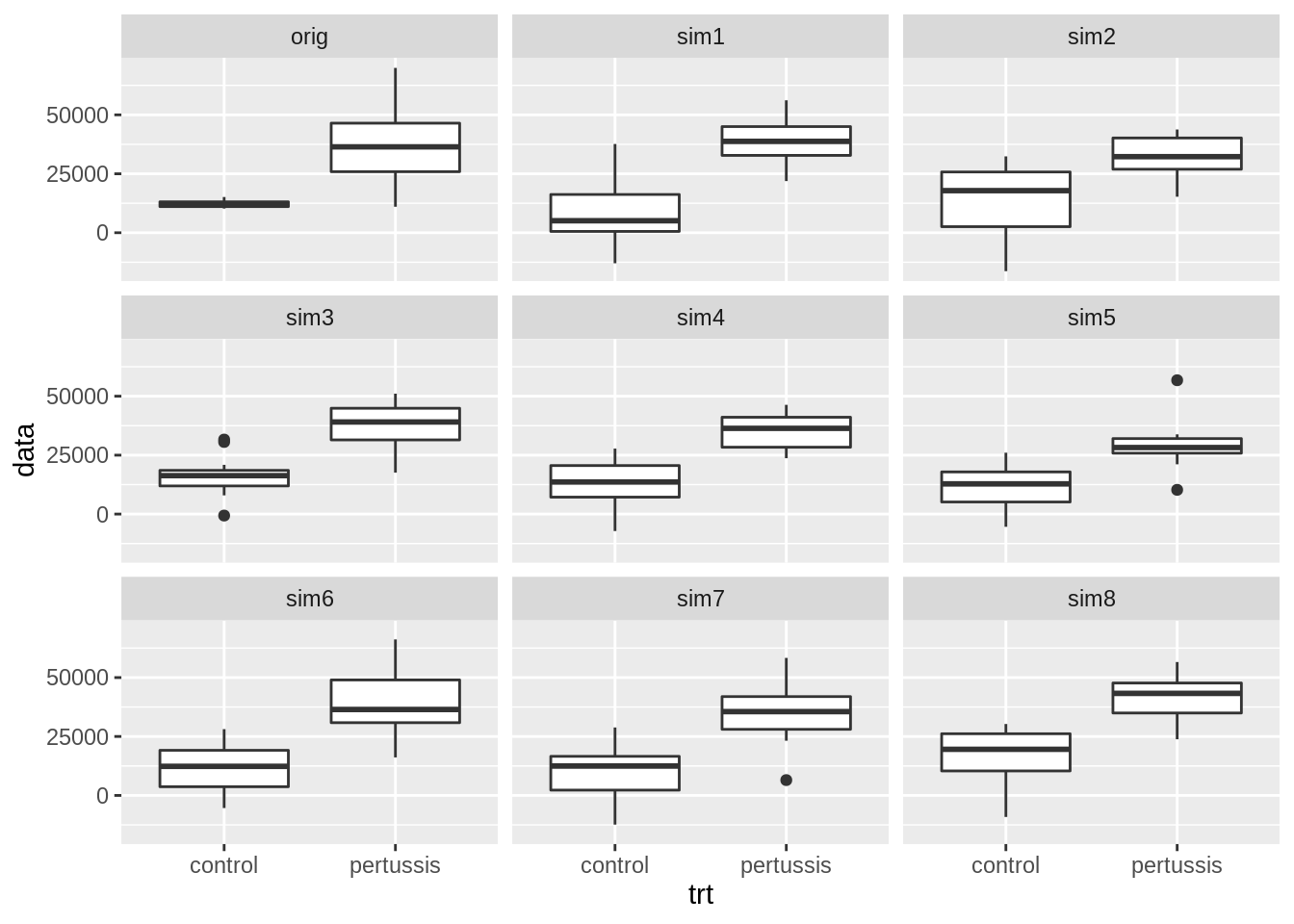
We observe that the difference in variability of the original observations (top left plot) is larger than in the each simulations. Indicating that there is indeed evidence that the variances in each group differ.

6.3 Evaluation of normality

6.3.1 Control group

normSim %>%
  gather(samp, data, -trt) %>%
  filter(trt == "control") %>%
  ggplot(aes(sample = data)) +
  geom_qq() +
  geom_qq_line() +
  facet_wrap(~samp)

6.3.2 Pertussis group

normSim %>%
  gather(samp, data, -trt) %>%
  filter(trt == "pertussis") %>%
  ggplot(aes(sample = data)) +
  geom_qq() +
  geom_qq_line() +
  facet_wrap(~samp)

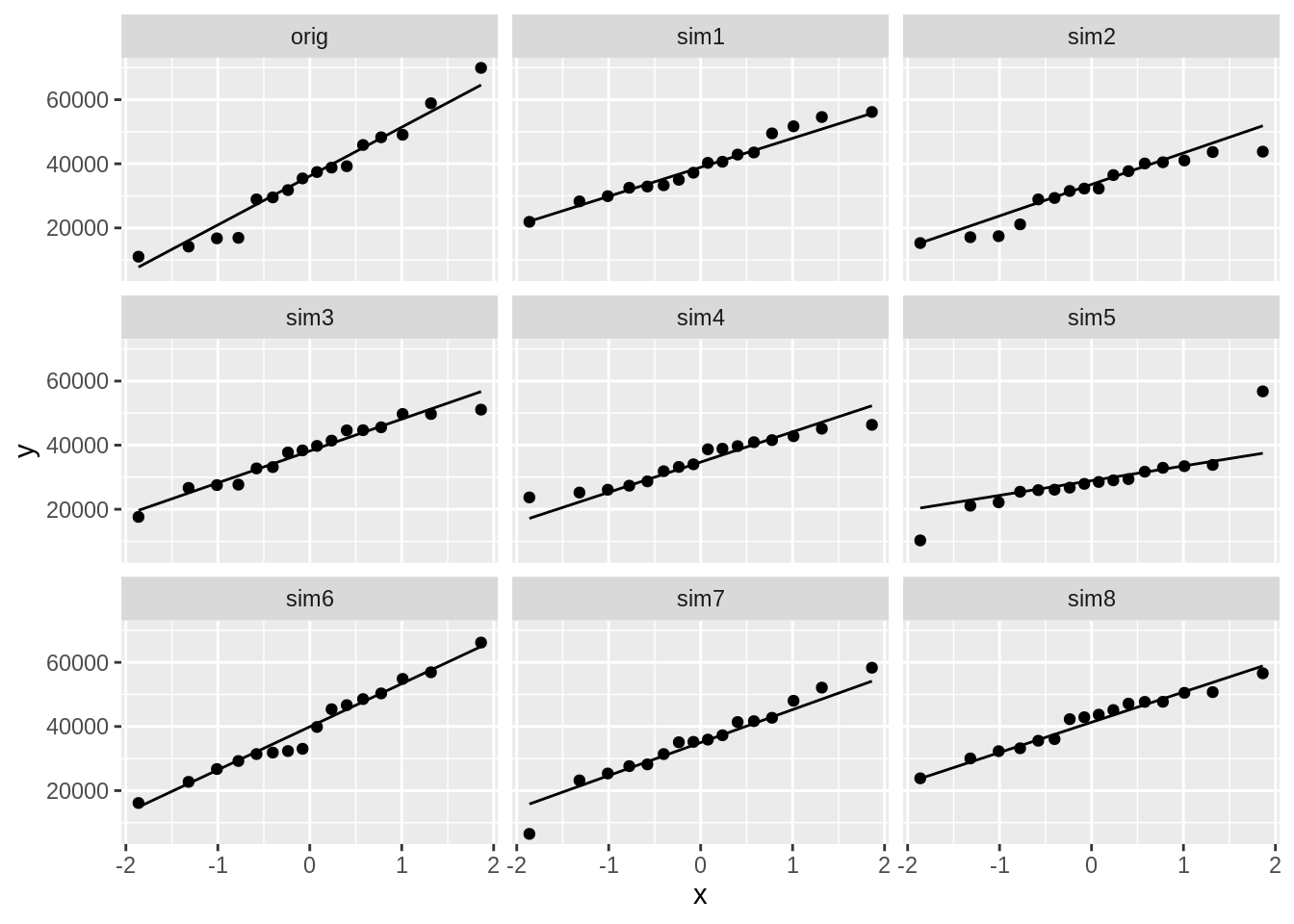
The data in each group does not show larger deviations from normality than what we observe in each of the eight datasets that were simulated under the model assumptions.

---

This work is licensed under the CC BY-NC-SA 4.0 licence.