9. Nonparametric Statistics - Wilcoxon-Mann-Withney test

#Intro

Inference was only correct if distributional assumptions were satisfied

• e.g Normal distribution

• equal variance

• The \(p\)-value: \(\text{P}_0\left[ \vert T\vert \geq \vert t \vert \right]\).

  • Calculated using the null distribution of \(T\) that we derived under the assumptions
  • In correct if assumptions are violated

• \(95\%\) CI also builds upon these assumptions. If they are invalid then the intervals will not contain the population parameter with 95% probability.

• Asymptotic theory is more difficult to place: the \(t\)-test is asymptotically non-parametric because for very large samples the distributional assumptions of normality are no longer important.

• If assumptions hold the parametric approach

  • more efficient: larger power with same sample size + smaller CI.
    
  • more flexible: easier to analyse data with complex designs

---

0.1 Cholesterol voorbeeld

• Cholesterol concentration in blood measured for
  • 5 patients (group=1) two days upon a stroke
  • 5 healthy subject (groep=2).
• Is cholesterol concentration of hart patients and healthy subjects on average different?

chol <- read_tsv("https://raw.githubusercontent.com/GTPB/PSLS20/master/data/chol.txt")
chol$group <- as.factor(chol$group)
nGroups <- table(chol$group)
n <- sum(nGroups)
chol

---

• Possibly outliers
• Difficult to assess distributional assumptions when only 5 observations are available.

1 Rank Tests

• Important group of non-parametric test
  • Non-parametric,
  • Exact \(p\)-values using a permutation null distribution.
  • No need for separate permutation distribution for each new dataset.
    
  • Permutation null distribution of rank tests only depends on sample size
  • Robust to outliers

---

#Ranks

Rank tests start from rank-transformed data.

• Let \(Y_1, \ldots, Y_n\).
• In the absence of ties \[R_i=R(Y_i) = \#\{Y_j: Y_j\leq Y_i; j=1,\ldots, n\}\]
• Smallest observation has rank 1, second smallest rank 2, … , largest observation gets rank \(n\)

chol$cholest

 [1] 244 206 242 278 236 188 212 186 198 160

rank(chol$cholest)

 [1]  9  5  8 10  7  3  6  2  4  1

---

1.1 ties

Sometimes ties occur: two observations with identical values

withTies=c(403,507,507,610,651,651,651,830,900)
rank(withTies)

[1] 1.0 2.5 2.5 4.0 6.0 6.0 6.0 8.0 9.0

• Ties: 507 occurs twice, 651 occurs 3 times

• If ties occur midranks are used.

• midrank of observation \(Y_i\) becomes \[\begin{eqnarray*} R_i &=& \frac{ \#\{Y_j: Y_j\leq Y_i\} + ( \#\{Y_j: Y_j < Y_i\} +1)}{2}. \end{eqnarray*}\]

---

1.2 Ranks of pooled sample

• Let \(Y_{ij}\), \(i=1,\ldots, n_j\) be observations from two treatment groups \(j=1,2\).
• They can also be represented by \(Z_1,\ldots, Z_n\) (\(n=n_1+n_2\)), the outcomes of the pooled sample

t(chol)

        [,1]  [,2]  [,3]  [,4]  [,5]  [,6]  [,7]  [,8]  [,9]  [,10]
group   "1"   "1"   "1"   "1"   "1"   "2"   "2"   "2"   "2"   "2"  
cholest "244" "206" "242" "278" "236" "188" "212" "186" "198" "160"

z=chol$cholest
z

 [1] 244 206 242 278 236 188 212 186 198 160

rank(z)

 [1]  9  5  8 10  7  3  6  2  4  1

---

2 Wilcoxon-Mann-Whitney Test

Simultaneously developed by Wilcoxon, and, Mann and Whitney: Wilcoxon-Mann-Whitney, Wilcoxon rank sum test or Mann-Whitney U test

2.1 hypotheses

Under \(H_0\) the distributions of the two groups are equal \[H_0: f_1=f_2\]

Under the alternative \(H_1\) the distributions differ in location \[H_1: \mu_1\neq \mu_2\]

\(H_1\) assumes location-shift, we will relax this assumption later on.

2.2 Test statistic

Classic T-test: difference in sample means \(\bar{Y}_1-\bar{Y}_2\).

Here: Difference in sample means based on rank transformed data

Ranks based on the pooled sample (upon joining the observations from the two groups): \(R_{ij}=R(Y_{ij})\) is de rank of observation \(Y_{ij}\) in the pooled sample.

\[ T = \frac{1}{n_1}\sum_{i=1}^{n_1} R(Y_{i1}) - \frac{1}{n_2}\sum_{i=1}^{n_2} R(Y_{i2}) . \]

• Under \(H_0\) we expect the average rank of the first group to be close to that of the second group so \(T\) is close to zero.

• Under \(H_1\) we expect the mean ranks to differ so that \(T\) deviates from zero.

• It is sufficient to only calculate \[S_1=\sum_{i=1}^{n_1} R(Y_{i1})\].

• \(S_1\) is the sum of the ranks of the first group: rank sum test.

• This holds because \[ S_1+S_2 = \text{sum of all ranks} = 1+2+\cdots + n=\frac{1}{2}n(n+1). \]

• \(S_1\) (or \(S_2\)) is a good test statistic

• Use permutations to determine the exact permutation distribution. (Permute the ranks between the groups)

• For a given \(n\) and no ties the rank transformed data is always \[1, 2, \ldots, n\]

• For given \(n_1\) en \(n_2\) the permutation distribution is always the same!

• With current computing power this is not so important any more.

---

2.3 Standardized statistic

Often the standardized test statistic is used \[ T = \frac{S_1-\text{E}_{0}\left[S_1\right]}{\sqrt{\text{Var}_{0}\left[S_1\right]}}, \]

• with \(\text{E}_{0}\left[S_1\right]\) and \(\text{Var}_{0}\left[S_1\right]\) the expect mean and variance of S1 under \(H_0\).

• Under \(H_0\) \[ \text{E}_{0}\left[S_1\right]= \frac{1}{2}n_1(n+1) \;\;\;\;\text{ en }\;\;\;\; \text{Var}_{0}\left[S_1\right]=\frac{1}{12}n_1n_2(n+1). \]

• Under \(H_0\) and when \(\min(n_1,n_2)\rightarrow \infty\) \[ T = \frac{S_1-\text{E}_{0}\left[S_1\right]}{\sqrt{\text{Var}_{0}\left[S_1\right]}} \rightarrow N(0,1). \]

Asymptotically the standardised statistic follows a standard normal distribution!

---

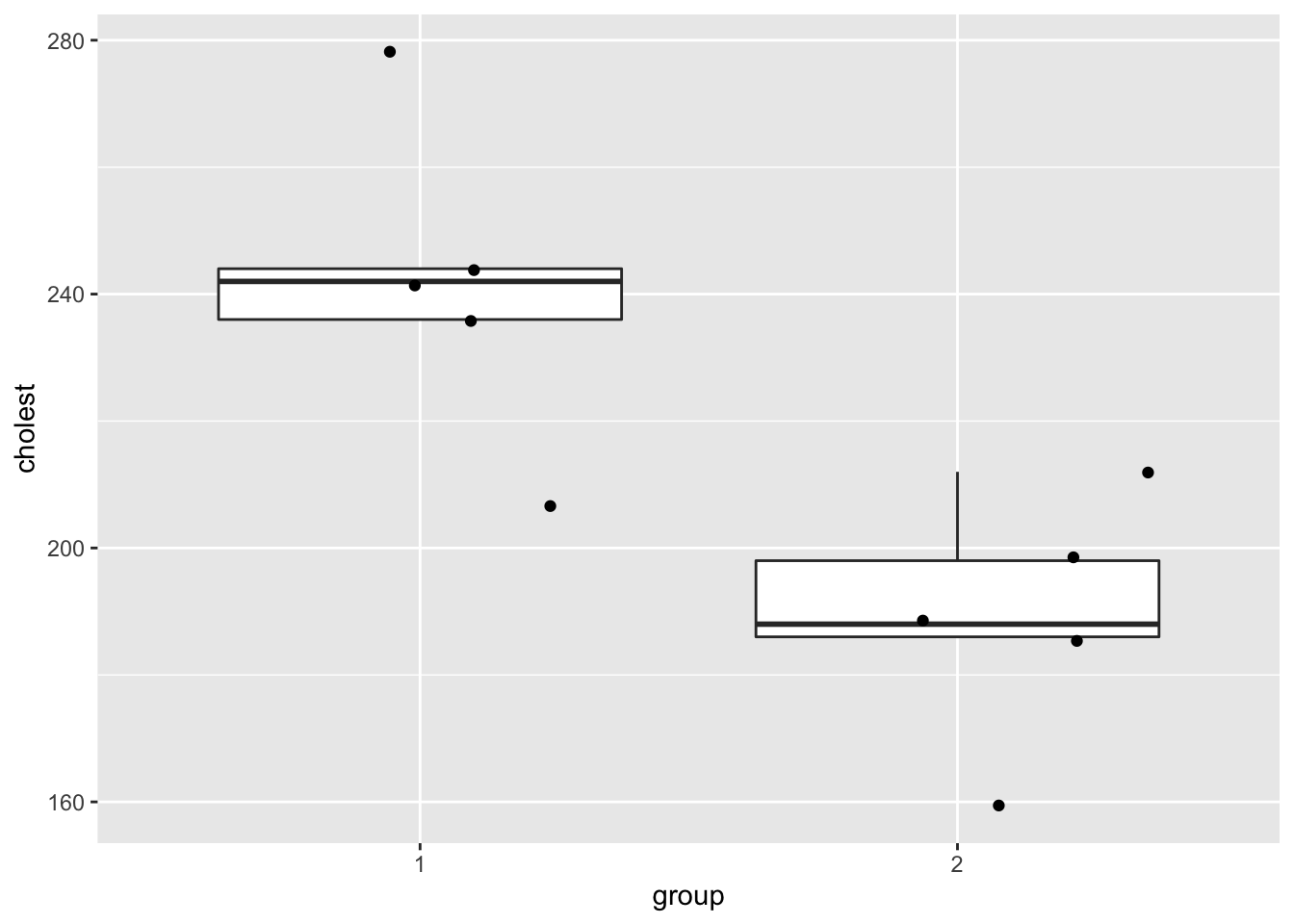
2.4 Cholesterol example

We illustrate the result for the cholesterol example using the R function wilcox.test.

wilcox.test(cholest~group,data=chol)

    Wilcoxon rank sum exact test

data:  cholest by group
W = 24, p-value = 0.01587
alternative hypothesis: true location shift is not equal to 0

• We reject \(H_0\) (\(p=\) 0.016 \(<0.05\))

• The output shows \(W=\) 24?

• Lets calculate

S1 <- sum(rank(chol$cholest)[chol$group==1])
S1

[1] 39

S2 <- sum(rank(chol$cholest)[chol$group==2]) 
S2

[1] 16

• Where does \(W=\) 24 comes from?

---

2.5 Mann and Whitney test

Mann and Whitney test in absence of ties: \[ U_1 = \sum_{i=1}^{n_1}\sum_{k=1}^{n_2} \text{I}\left\{Y_{i1}\geq Y_{k2}\right\}. \]

• with \(\text{I}\left\{.\right\}\) an indicator that equals 1 if the expression is true and is zero otherwise.

• U counts how many times an observation of the first group is larger or equal to an observation from the second group.

y1=subset(chol,group==1)$cholest
y2=subset(chol,group==2)$cholest
u1Hlp=sapply(y1,function(y1i,y2) {y1i>=y2},y2=y2)
colnames(u1Hlp)=y1;rownames(u1Hlp)=y2

u1Hlp

     244   206  242  278  236
188 TRUE  TRUE TRUE TRUE TRUE
212 TRUE FALSE TRUE TRUE TRUE
186 TRUE  TRUE TRUE TRUE TRUE
198 TRUE  TRUE TRUE TRUE TRUE
160 TRUE  TRUE TRUE TRUE TRUE

U1=sum(u1Hlp); U1

[1] 24

It can be shown that \(U_1 = S_1 - \frac{1}{2}n_1(n_1+1).\)

S1-nGroups[1]*(nGroups[1]+1)/2

 1 
24 

1. \(U_1\) en \(S_1\) contain the same information
2. \(U_1\) is also a rank statistic, and
3. Exact test based on \(U_1\) and \(S_1\) are equivalent.

---

2.6 Probabilistic index

• \(U_1\) has a better interpretation feature
• Let \(Y_j\) a random observation from group \(j\) (\(j=1,2\)). Then \[\begin{eqnarray*} \frac{1}{n_1n_2}\text{E}\left[U_1\right] &=& \text{P}\left[Y_1 \geq Y_2\right]. \end{eqnarray*}\]

So we can estimate the probability by calculating the mean of all indicator variable values \(\text{I}\left\{Y_{i1}\geq Y_{k2}\right\}\). Note, that we did \(n_1 \times n_2\) comparisons

mean(u1Hlp)

[1] 0.96

U1/(nGroups[1]*nGroups[2])

   1 
0.96 

• Probability \(\text{P}\left[Y_1 \geq Y_2\right]\) is referred to as the probabilistic index.

• It is the probability that a random observation of the first group is larger or equal than a random observation of the second group
  

• If \(H_0\) holds \(\text{P}\left[Y_1 \geq Y_2\right]=\frac{1}{2}\).

• R function wilcox.test does not return the Wilcoxon rank sum statistic. It returns the Mann-Whitney statistic \(U_1\).

• Lets revisit the result

wTest<-wilcox.test(cholest~group,data=chol) 
wTest

    Wilcoxon rank sum exact test

data:  cholest by group
W = 24, p-value = 0.01587
alternative hypothesis: true location shift is not equal to 0

U1

[1] 24

probInd=wTest$statistic/prod(nGroups) 
probInd

   W 
0.96 

Because \(p=\) 0.0159 \(<0.05\) we conclude at the \(5\%\) significance level that the mean cholesterol level of hart patients is larger then that of healthy subjects.

• Note that we have assumed that the location-shift model is valid in this conclusion.
• We also know that higher cholesterol level are more likely for hart patients then for healthy subjects and this probability is \(U1/(n_1\times n_2)=\) 96%.
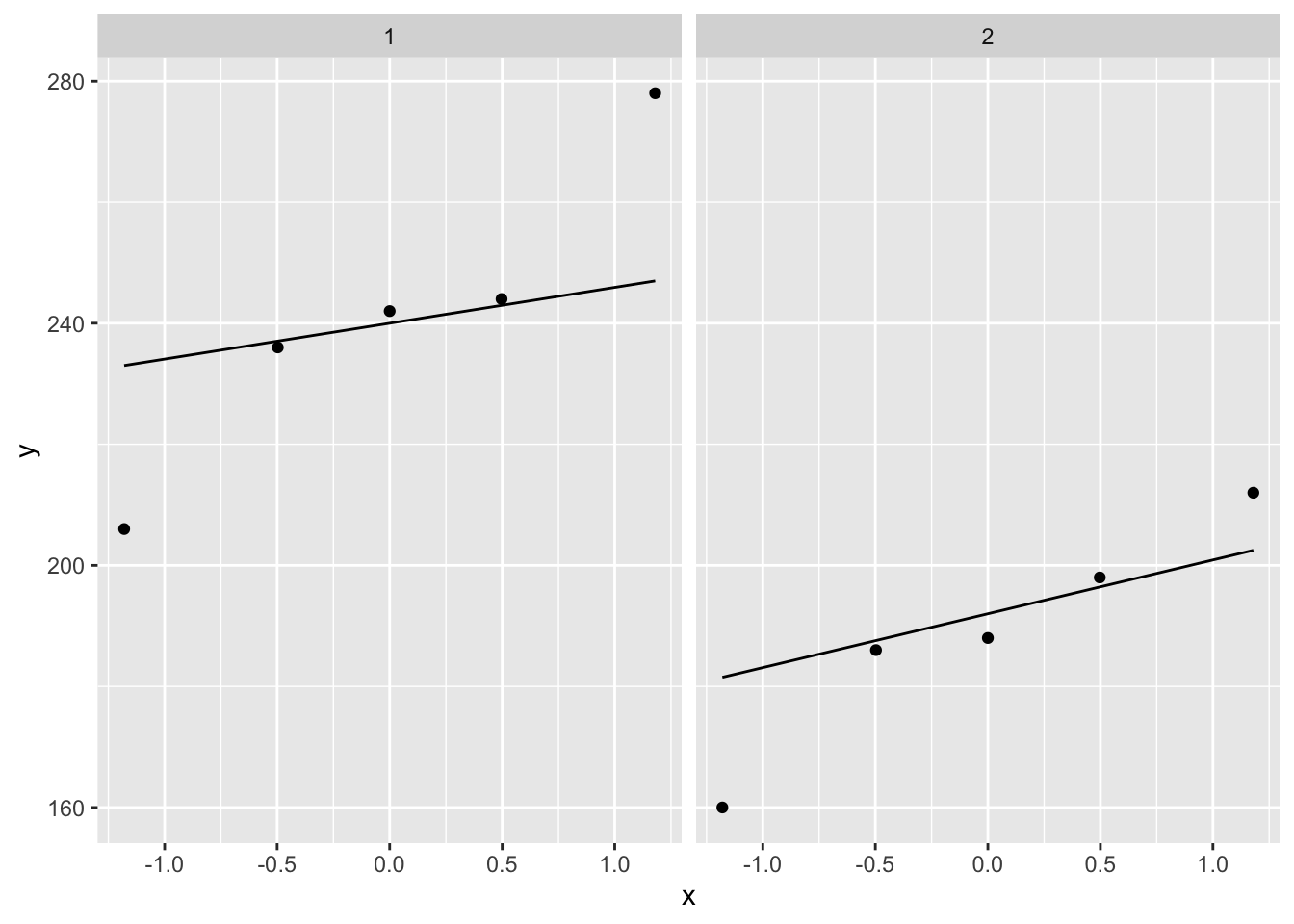
• We should assess the location shift assumption. But this is not possible with only 5 observations.

Without the location-shift assumption the conclusion in terms of the probabilistic index remains valid!

• So when we do not assume location shift we test for

\[H_0: F_1=F_2 \text{ vs } H_1: P[Y_1 \geq Y_2] \neq 0.5.\]

2.7 Conclusion

There is a significant difference in the distribution of the cholesterol concentration of hart patients two days upon a stroke and that of healthy subject ((\(p=\) 0.0159). It is more likely to observe higher cholesterol levels for hart patients then for healthy subjects. The point estimator for this probability is 96%.

---

This work is licensed under the CC BY-NC-SA 4.0 licence.