GWAS background

1 Background

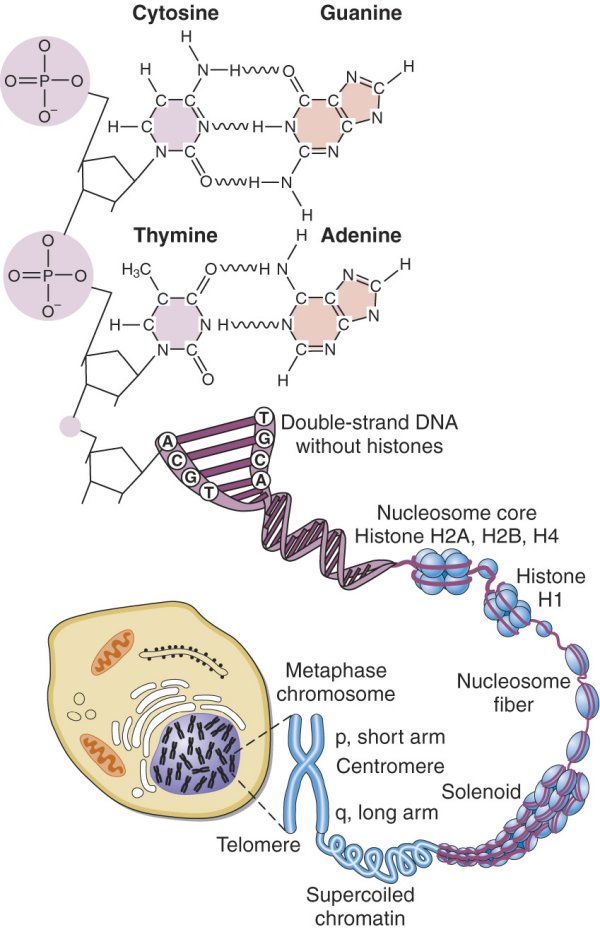
1.1 DNA

• 6 Billion base pairs: 3 billion from father and 3 billion from mother
• Organised in \(2 \times 23\) chromosomes of length 50 - 250 milion bp

1.2 Transcription / translation

1.3 Variation in DNA

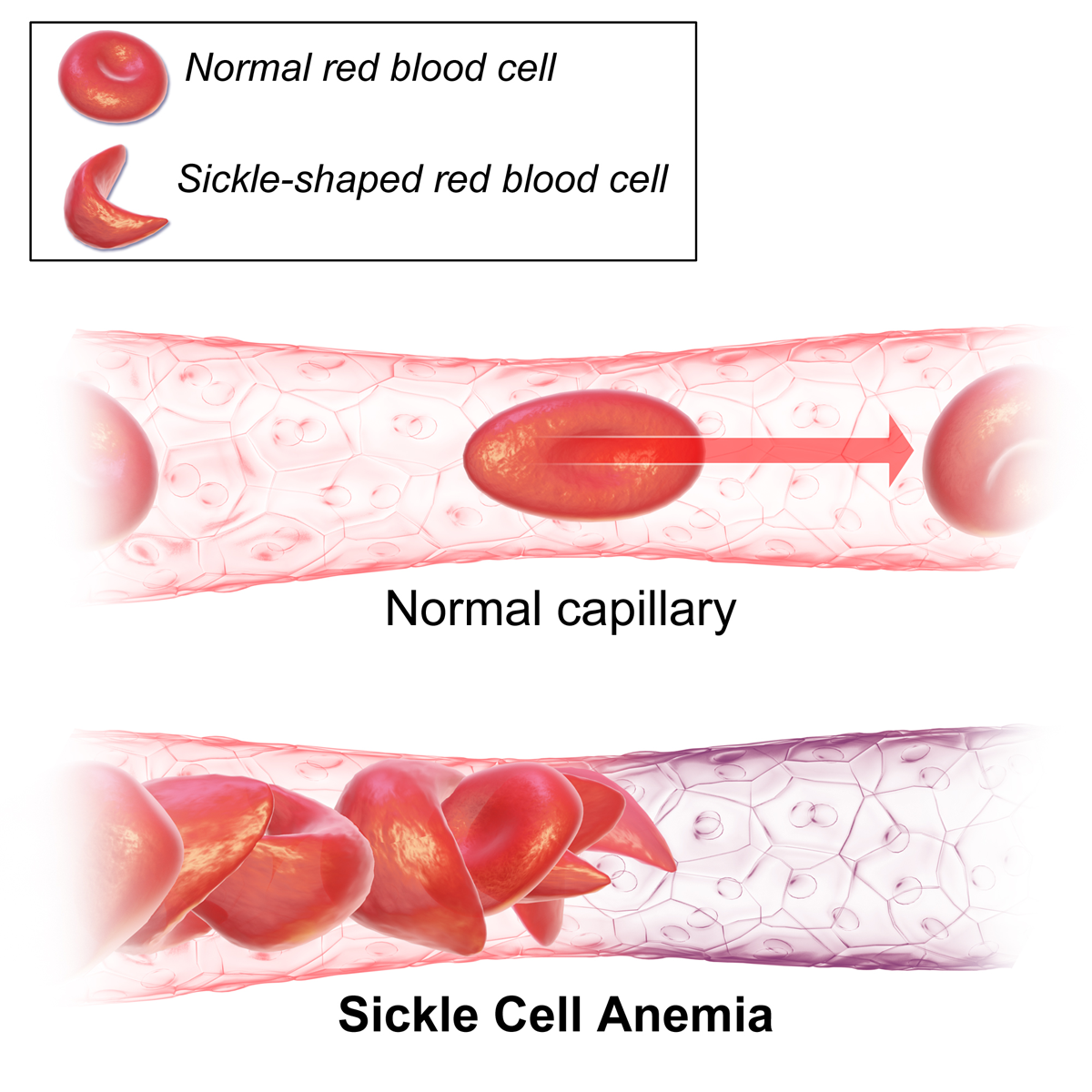
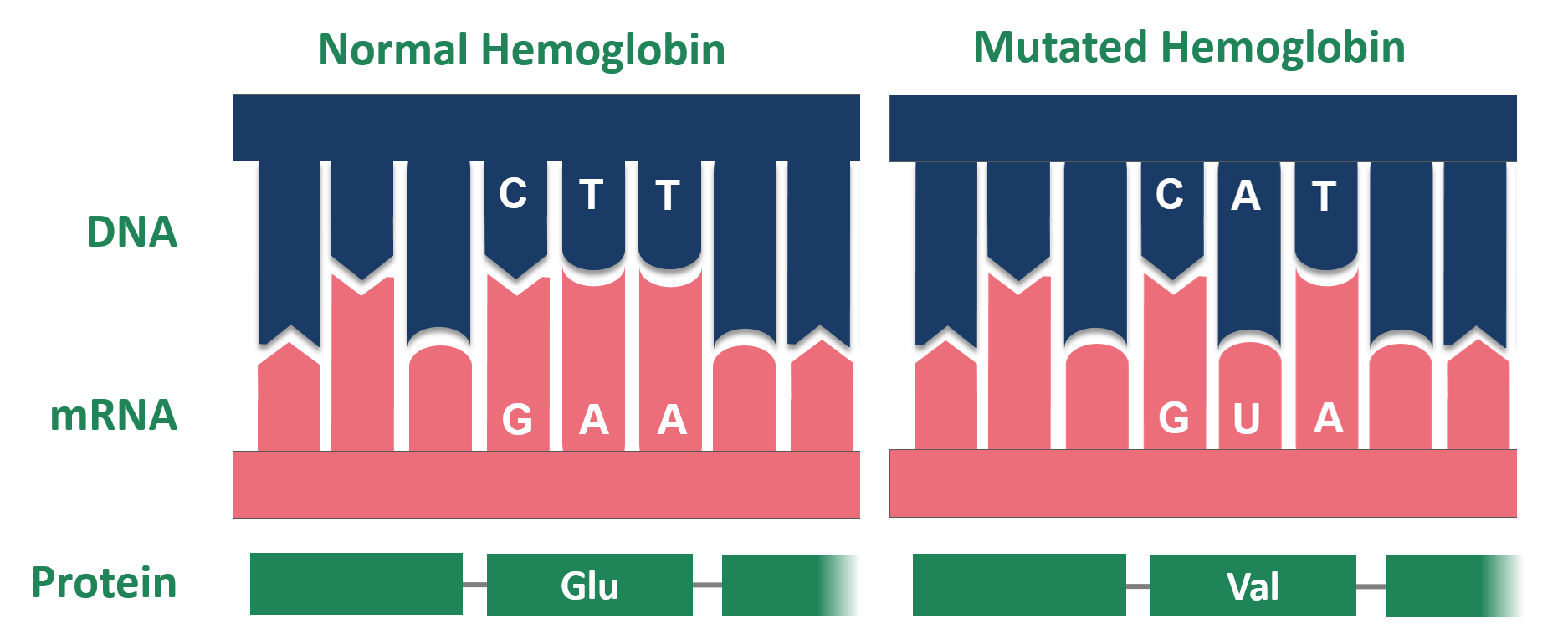
• 90% of variation in DNA are SNP: single nucleotide polymorphism. Different base at a single position in the DNA

• Humans: \(\pm\) 5 million SNPs

• Most of them are neutral: high redundancy in the genomic code

• Sometimes they are not neutral:

• Genomic recombination of parental chromosomes when producing germ cells.

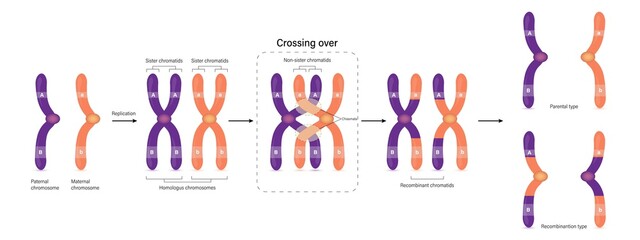
• Linkage disequilibrium: SNPs often occur together because of genomic recombination!

1.4 GWAS in University of Bergen

• GWAS: Genome Wide Association Studies
• Studies in large cohorts
• Use SNPs to identify genes associated with a particular trait: e.g. birth weight, pacenta weight, BMI, … .

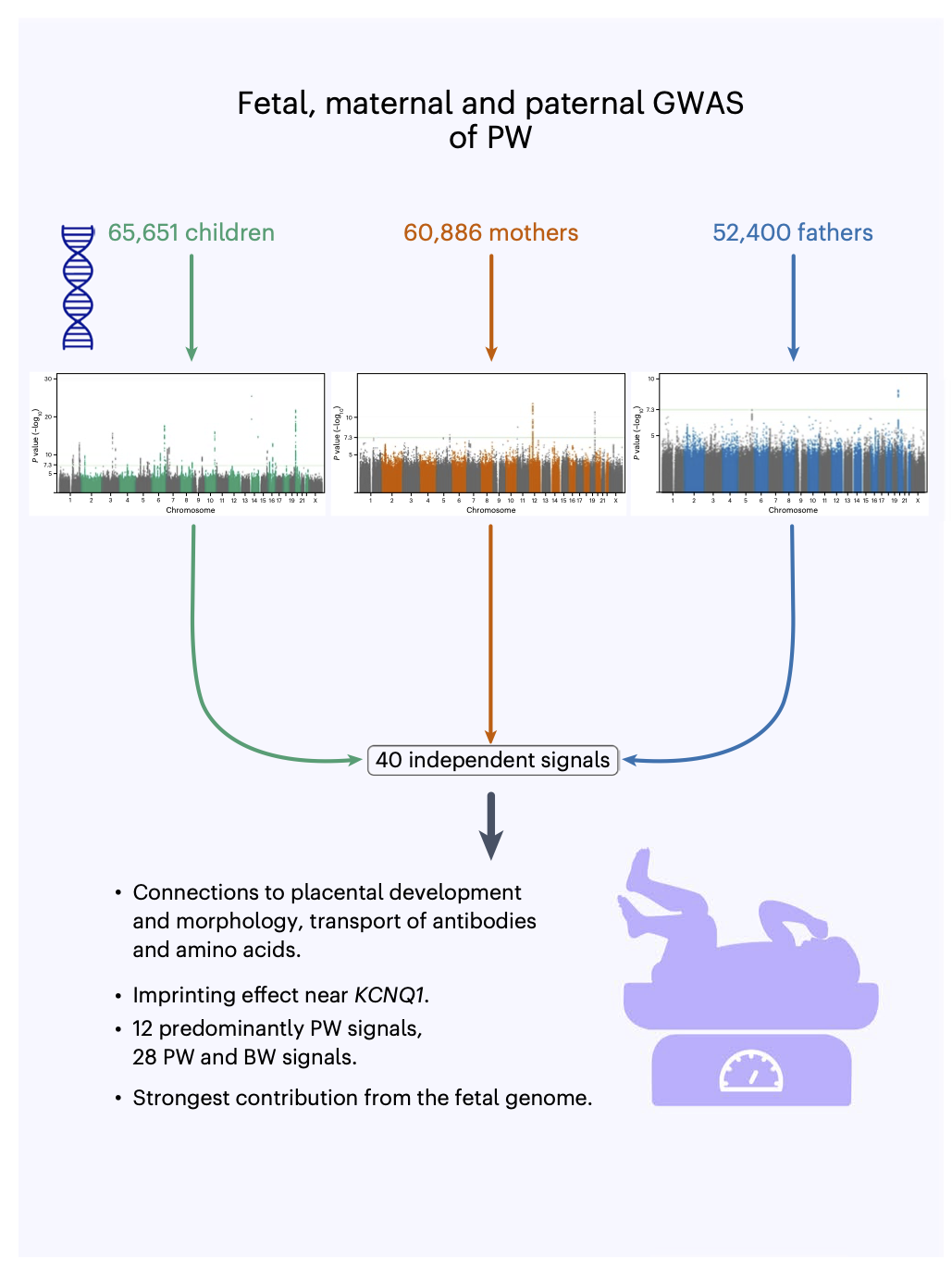
2 Linear models for GWAS

In GWAS one often corrects for population stratification using the following linear model.

\[ \tag{1} \mathbf{y} = \mathbf{x}_\text{test}\beta_\text{test} + \mathbf{X}_c\boldsymbol{\beta}_c + \mathbf{X}_\text{PCA} \boldsymbol{\beta}_\text{PCA} +\boldsymbol{\epsilon} \] with

• \(\mathbf{y}\) an \(N\times1\) vector of the phenotype
• \(\mathbf{x}_\text{test}\) an \(N\times1\) vector with the genotype for the candidate SNP
• \(\beta_\text{test}\) the association of candidate SNP and the phenotype
• \(\mathbf{X}_c\) an \(N\times C\) matrix with the covariate pattern for \(C\) known covariates (vector of ones (intercept), age, gender, batch,…)
• \(\boldsymbol{\beta}_c\) the \(p\times 1\) vector of parameters modeling the association of the p covariates and the phenotype.
• \(\mathbf{X}_\text{PCA}\) an \(N\times p\) matrix with p PCs used to correct for population stratification
• \(\boldsymbol{\epsilon}\) an \(N\times 1\) vector with environmental residuals that are assumed to be i.i.d. \(\epsilon_i \sim N(0,\sigma_u^2)\) with \(i = 1\ldots N\)

Let \(\mathbf{Z}\) be an \(N\times M\) genetic relationship matrix with all \(M\) normalised genotypes. Then with the SVD we can decompose \(\mathbf{Z}\)

\[ \mathbf{Z} = \mathbf{U}\boldsymbol{\Delta}\mathbf{V}^T \] Note, that the \(N\times M\) matrix \(\mathbf{V}\) are also the M PCs of an PCA. So we can approximate \(\mathbf{Z}\) using a truncated PCA, e.g. by using the first \(p\) PCs. \[ \mathbf{Z}_p = \mathbf{U}_{p} \boldsymbol{\Delta}_p\mathbf{V}^T_p \] with

\[ \mathbf{X}_\text{PCA} = \mathbf{U}_{p} \boldsymbol{\Delta}_p \] the scores on the first p PCs that can be used to correct for population stratification.

3 Linear mixed model for GWAS

3.1 Specification

\[ \tag{1} \mathbf{Y} = \mathbf{x}_\text{test}\beta_\text{test} + \mathbf{X}_c\boldsymbol{\beta}_c + \mathbf{Z}_{GRM}\mathbf{u} +\boldsymbol{\epsilon} \] with

• \(\mathbf{Y}\) an \(N\times1\) vector of the phenotype
• \(\mathbf{x}_\text{test}\) an \(N\times1\) vector with the genotype for the candidate SNP
• \(\beta_\text{test}\) the association of candidate SNP and the phenotype
• \(\mathbf{X}_c\) an \(N\times p\) matrix with the covariate pattern for \(C\) known covariates (vector of ones (intercept), age, gender, batch,…)
• \(\boldsymbol{\beta}_c\) the \(p\times 1\) vector of parameters modeling the association of the p covariates and the phenotype.
• \(\mathbf{Z}\) an \(N\times M\) genetic relationship matrix (GRM) with all normalised genotypes
• \(\mathbf{u}\) an \(M\times 1\) vector with i.i.d. random effect for each SNP \(\mathbf{u}\sim \text{MVN}(0,\mathbf{I}\sigma_u^2)\)
• \(\boldsymbol{\epsilon}\) an \(N\times 1\) vector with environmental residuals that are assumed to be independent of \(\mathbf{u}\) and i.i.d. \(\boldsymbol{\epsilon}\sim \text{MVN}(0,\mathbf{I}\sigma_\epsilon^2)\)

Random effects are used to model the correlation structure in the data. They imply a certain covariance structure of \(\mathbf{y}\)

3.2 Covariance structure

Covariance structure of \(\mathbf{y}\) implied by GWAS mixed model:

\[ \begin{array}{ccl} \text{var}\left[\mathbf{Y}\right] &=& \text{var}\left[\mathbf{x}_\text{test}\beta_\text{test} + \mathbf{X}_c\boldsymbol{\beta}_c + \mathbf{Z}_\text{GRM}\mathbf{u} +\boldsymbol{\epsilon}\right]\\\\ &\updownarrow& \mathbf{u} \perp \boldsymbol{\epsilon}\\\\ &=& \text{var}[\mathbf{Z}_\text{GRM}\mathbf{u}] + \text{var}[\boldsymbol{\epsilon}]\\\\ &=&\mathbf{Z}_\text{GRM}\text{var}[\mathbf{u}]\mathbf{Z}_\text{GRM}^T + \mathbf{I} \sigma^2\\\\ &=&\mathbf{Z}_\text{GRM}\mathbf{I}\sigma^2_u\mathbf{Z}_\text{GRM}^T + \mathbf{I} \sigma^2_\epsilon \\\\ &=&\mathbf{Z}_\text{GRM}\mathbf{Z}_\text{GRM}^T \sigma^2_u+ \mathbf{I} \sigma^2_\epsilon \end{array} \]

Note that the model is often also written in another way:

\[ \tag{1} \mathbf{Y} = \mathbf{x}_\text{test}\beta_\text{test} + \mathbf{X}_c\boldsymbol{\beta}_c + \mathbf{g} +\boldsymbol{\epsilon} \]

• with \(\mathbf{g} \sim \text{MVN}(\mathbf{0},\mathbf{K}\sigma^2_g)\)

• \(\mathbf{K}\) the \(N \times N\) empirical kinship matrix

\[ \mathbf{K} = \frac{\mathbf{Z}_\text{GRM}\mathbf{Z}^T_\text{GRM}}{M} \]

• \(\sigma_g^2\) the polygenic variance \(\sigma_g^2=M\sigma_u^2\)

3.3 Main advantages of LMM method

1. Better control of false positive associations by correcting for population or relatedness structure
2. An increase in power:

• Through the correction for this structure.
• by conditioning on associated loci other than the candidate locus.

3.4 Pitfalls of LMM

1. Computational complexity:

• \(M > 500.000\), \(N > 70000\)
• Building the GRM (\(M \times M\) matrix)
• Estimating the mean and variance components for each of the \(M\) candidate SNP!
• Association statistics for each variant (for each SNP!)

2. Loss in power when the candidate marker is included in the GRM

3. Using a small subset of markers in the GRM can compromise correction for stratification

---

This work is licensed under the CC BY-NC-SA 4.0 licence.